
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анализ взаимосвязи между параметрами статистической совокупностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В подразделе описана сущность метода корреляционно регрессионного анализа, его практическое значение и методика расчета коэффициентов корреляции и регрессии. Вопросы для изучения: — Когда возникает необходимость применения корреляционного анализа? —В чем заключается адекватность выбора рангового или линейного коэффициента корреляции? —Что характеризует коэффициент регрессии? Цель: обосновать необходимость использования метода корреляционно регрессионного анализа; научить рассчитывать ρ и анализировать коэффициенты корреляции и регрессии. Все изменения, которые происходят в природе, являются взаимосвязанными и взаимообусловленными. Изменчивость определенного признака как следствие изменчивости других параметров, в свою очередь, обуславливают изменчивость других признаков. Однако, указанная зависимость в отдельных ситуациях проявляется по-разному. Функциональная связь часто присутствует при изучении химических и физических явлений, в математике, геометрии.
В медико-биологических исследованиях зависимость между отдельными параметрами не является функциональной связью. При изменении одного признака невозможно абсолютно точно спрогнозировать величину, на которую изменяются другие. Примером такой корреляционной связи является зависимость веса и роста детей, тяжести патологии и сроков лечения, концентрации вредных веществ в рабочей зоне и уровень заболеваемости работников.
Определение характера связи между определенными параметрами проводят путем расчета коэффициента корреляции, который в зависимости от его характера и формы представления данных может быть рассчитан разными методами.
Таблица 26.
Коэффициент парной корреляции отображает характер связи 2 признаков. Он может быть рассчитан при сопоставлении двух рядов в виде рангового коэффициента корреляции (ρ ) и линейного коэффициента корреляции (r).
Корреляционная зависимость различается по направлению, силе и форме связи (таблица 26). По направлению корреляционная связь может быть положительной ("прямой") и отрицательной ("обратной"). Степень, сила или теснота корреляционной связи определяется по величине коэффициента корреляции. Сила связи не зависит от ее направленности и определяется по абсолютному значению коэффициента корреляции.
Максимальное возможное абсолютное значение коэффициента корреляции r = 1,00; минимальное r = 0,00.
Коэффициент ранговой корреляции Спирмена - это непараметрический метод, который используется с целью статистического изучения связи между явлениями. Практический расчет коэффициента ранговой корреляции Спирмена включает следующие этапы: 1) Определить каждому из признаков их порядковый номер (ранг) по возрастанию (или убыванию). 2) Определить разности рангов каждой пары сопоставляемых значений. 3) Возвести в квадрат каждую разность и суммировать полученные результаты. 4) Вычислить коэффициент корреляции рангов по формуле:
ρ =1-
где
Методика расчета на примере характеристики взаимосвязи стажа работы работников угольной промышленности и частотой заболеваний на бронхит в них.
При большом числе наблюдений (n> 100) средняя погрешность рангового коэффициента корреляции может быть определена по формуле: mp=
Оценка достоверности коэффициента корреляции проводиться по тем же принципами, что используются для других показателей с учетом числа наблюдений (числа степеней свободы вариационных рядов n` = n – 2).
Один из методов расчета коэффициента линейной корреляции был предложен К.Пирсоном. Формула для подсчета коэффициента корреляции Пирсона такова: r = X и Y – варианты сравниваемых вариационных рядов; dx и dy – отклонение каждой варианты от своей средней арифметческой
Таблица 28. Зависимость между составом железа в крови и уровнем гемоглобина в крови.
Расчет линейного коэффициента корреляции: 1. Определяют средние значения для каждого ряда (Хх, Ху). 2. Определяют отклонение каждого из значений ряда от средней величины (dх, dу). 3. Возводят определенные отклонения в квадрат и определяют их суммы:
Достоверность полученного результата определим соотношением t = r / mr, где mr при малом числе наблюдений (n < 30) равняется: mr=
При большом числе наблюдений (n > 100) формула для расчета средней погрешности коэффициента корреляции может иметь вид: m=
Прямолинейная корреляционная связь между параметрами характеризуется тем, что каждому из одинаковых измерений одного показателя отвечает определено среднее значение другого показателя. Данную зависимость можно описать коэффициентом регрессии. Рассчитывается коэффициент регрессии по формуле: Rx/y=rxy* Где: Rx/y - коэффициент регрессии от Х до У; rxy - коэффициент корреляции;
Выше приведенные методики расчета парных коэффициентов корреляции являются основой и только первым этапом многофакторного корреляционной анализа. Парные коэффициенты показывают характер связи (общего, «неочищенного») между исследуемыми параметрами без учёта влияния других факторов. Оценивание «чистой» взаимосвязи в многофакторных моделях определяется на основе парциальных коэффициентов корреляции, основой для расчета которых являются парные и множественные коэффициенты. В практике медицинских исследований достаточно часто возникает вопрос об определении влияния нескольких разных факторов на определенное явление, например, на частоту осложнений при родах влияет возраст женщины, наличие акушерской и экстрагенитальной патологии, качество предоставления медицинской помощи и др. В таких случаях для выявления комбинированного влияния нескольких факторов на размер исследуемого явления пользуются методом множественной корреляции. Использование этого метода проводиться в несколько этапов. Математический аппарат данного анализа является достаточно сложным и выходит за пределы программы подготовки врачей. В настоящее время существует много специализированных программ статистического анализа, которые позволяют рассчитать множественный коэффициент корреляции для определенной совокупности показателей. Важным является оценка результата: в случае, когда сумма парциальных коэффициентов корреляции меньше величины множественного коэффициента корреляции, мы можем говорить о потенцируемом действии исследуемых параметров относительно результативного признака. Иначе (что, по нашему опыту, случается чаще) мы можем отмечать параллельное влияние факторов с невыраженным взаимным потенцируемым эффектом с условия, когда сумма парциальных коэффициентов значительно превышает значение множественного коэффициента корреляции. Следовательно, множественный коэффициент корреляции отображает связь одновременно комплекса факторов с исследуемым результативным фактором (клиническими показателями и др.). Вопросы для контроля: 1.Что такое корреляционная связь? Чем она отличается от функциональной? 2.Дайте характеристику формы, направления и силы связи. 3.Что такое регрессия?
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 880; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.101.7 (0.008 с.) |


 - сумма квадратов разностей рангов, а
- сумма квадратов разностей рангов, а  - число парных наблюдений.
- число парных наблюдений.
 =1-6*2/5*(25-1)=
=1-6*2/5*(25-1)= 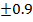 ВЫВОД: между стажем работы работников и частотой заболевания на бронхит выявлено сильную, прямую корреляционную связь.
Ошибка рангового коэффициента корреляции для нашего случая исчисляется по формуле:
m=
ВЫВОД: между стажем работы работников и частотой заболевания на бронхит выявлено сильную, прямую корреляционную связь.
Ошибка рангового коэффициента корреляции для нашего случая исчисляется по формуле:
m=  для нашего случая m1=0,245 и t=3,67, что, соответственно, выше граничных значений. Полученный результат позволяет сделать вывод о вероятности данного рангового коэффициента корреляции.
для нашего случая m1=0,245 и t=3,67, что, соответственно, выше граничных значений. Полученный результат позволяет сделать вывод о вероятности данного рангового коэффициента корреляции.









 =34.89
=34.89
 Вывод: между составом железа в крови и уровнем гемоглобина существует сильная прямая связь. Для нашего случая коэффициент вероятности=3,6, что свыше гранично допустимых значений при вероятности ошибки меньшей 0,05
Вывод: между составом железа в крови и уровнем гемоглобина существует сильная прямая связь. Для нашего случая коэффициент вероятности=3,6, что свыше гранично допустимых значений при вероятности ошибки меньшей 0,05




 и
и  средние квадратические отклонения рядов Х и У.
средние квадратические отклонения рядов Х и У. Х = 3,2 см и Ху = 30,7 кг;
Х = 3,2 см и Ху = 30,7 кг;  (кг)
Вывод: при изменении роста на 1 см вес мальчиков в среднем изменится на 1,47 кг. Определенный коэффициент регрессии можно использовать в уравнении регрессии при прогнозировании ситуации - какой вес в среднем будет отвечать возрасту мальчиков 140,0 см:
Вывод: возрасту мальчиков 140,0 см будет отвечать вес 34,8 кг.
(кг)
Вывод: при изменении роста на 1 см вес мальчиков в среднем изменится на 1,47 кг. Определенный коэффициент регрессии можно использовать в уравнении регрессии при прогнозировании ситуации - какой вес в среднем будет отвечать возрасту мальчиков 140,0 см:
Вывод: возрасту мальчиков 140,0 см будет отвечать вес 34,8 кг.



