
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 1. История становления и развития біостатистикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
РАЗДЕЛ 3. АНАЛИТИЧЕСКАЯ СТАТИСТИКА Относительные величины (статистические показатели). Метод стандартизации.
В подразделе описан метод стандартизации, его практическое значение и методика расчета стандартизованных показателей. Вопросы для изучения: —Какие выходные данные необходимы для применения метода стандартизации? —В чем заключается содержание четырех этапов метода стандартизации? —О чем свидетельствует изменение соотношения между фактическими и стандартизированными показателями? Цель: обосновать необходимость использования метода стандартизации; научить рассчитывать и анализировать стандартизированные показатели. Объективное сопоставление общих интенсивных показателей возможно лишь при условии качественной однородности сравниваемых групп. Так, например, показатели летальности в двух ожоговых отделениях можно сравнивать между собой при условии, что оба стационара имеют приблизительно одинаковый состав больных по ряду основных параметров — возрасту, полом больных, тяжестью патологии, сроками госпитализации и тому подобное. Если их состав отличается, сравнение общих интенсивных показателей, характеризующих силу и распространенность явления, усложнено. При этом на величину общего интенсивного показателя влияет состав оцениваемой клинико-статистической группы.
При проведении клинических исследований при изучении эффективности определенного метода лечения также необходимо формировать однородные в сравнимые группы. При использовании метода стандартизации рассчитывают стандартизированные (условные) показатели, которые могли бы быть при условии одинакового состава населения в сравниваемых группах. Практическая значимость метода стандартизации: • позволяет сравнить частоту однотипных явлений в неоднородных группах; • позволяет оценить влияние исследуемого фактора на величину общих показателей. Оценка влияния определенного фактора на величину общих интенсивных показателей базируется на динамике соотношения данных показателей при условии изменений в составе исследуемых групп. Если условно изменение состава сравниваемых групп по определенным критериям приводит к изменению соотношения общих интенсивных показателей (изменение знака между ними), то это дает возможность сделать вывод о значимости (влиянии) данного фактора для оценивания уровней исследуемых показателей. Существует три метода стандартизации: • прямой; • опосредствованный; • обратный. Выбор любого из методов определяется формой представления первичного материала, удобством и скоростью расчетов, данными предыдущих исследований. Прямой метод используют при наличии данных о составе населения и составе исследуемого явления по точным параметрам (возрастом, профессиями, сроками госпитализации, тяжестью заболевания, и тому подобное). Отсутствие данных о распределении определенного явления или небольшая численности групп при данном распределении, что снижает достоверность групповых показателей, является основанием для использования опосредствованного метода стандартизации. Отсутствие данных о составе населения предопределяет необходимость использования обратного метода. Самым распространенным в медико-биологических исследованиях является прямой метод стандартизации.
Рассмотрим использование прямого метода стандартизации, который проводится в четыре этапа, на примере сравнения уровней летальности больных с острой кишечной непроходимостью в двух больницах, которые были госпитализированы в разные часы от начала заболевания. I этап — расчет групповых и общих интенсивных показателей. Чтобы оценить уровень летальности больных в разных больницах, необходимо исключить неоднородность состава больных по сроку госпитализации. Сравнение общих показателей летальности больных в двух больницах позволяет сделать вывод о более высокой летальности больных в больнице Б. Но здесь отмечается более высокий удельный вес больных со сроками госпитализации свыше 24 часов, что соответственно, может предопределять высокий уровень летальности. Для определения действительного соотношения частоты осложнений необходимо сравнить состав больных по срокам госпитализации. Расчет проводится по таблице. 14.
Таблица 14. Расчет уровней летальности среди больных хирургических отделений больниц А и Б.(1 этап)
II этап — выбор и расчет стандарта. Стандартом в нашем примере является состав больных с острой кишечной непроходимостью в двух больницах. За стандарт можно принять: 1)состав одной из сравниваемых групп; 2) суммарный или средний состав обеих групп; 3) известный состав любой другой группы.
В нашем примере за стандарт принимаем суммарный состав больных по срокам госпитализации в обеих исследуемых больницах, допуская, что состав больных по срокам госпитализации в обеих больницах отвечает распределению, выбранному за стандарт (таблица. 15).
Таблица 15. Расчет стандарта.(2 этап)
III этап — расчет «ожидаемых» чисел летальности в соответствии со стандартом. Каждая из исследуемых больниц имеет фактические уровни летальности больных с разным сроком госпитализации. На данном этапе анализа можно определить, какой уровень летальности госпитализированных больных будет при условии стандартного (одинакового) их распределения. Расчет ведется по следующей схеме: • какая летальность больных с острой кишечной непроходимостью, которые были госпитализированы до 6 часов в больницу А, могла бы быть, если удельный вес этих госпитализированных по стандарту составляет 34,1 % больных, а фактическая летальность в данной группе составляет 12,2 % (в больнице Б - 10,0 %).
Больница А 12,2 - 100 / Х - 34,1 / Х = 4,2 Больница Б 10,0 - 100 / Х - 34,1 / Х = 3,4
Полный расчет «ожидаемых» чисел летальности в соответствии со стандартом приведен в таблице 16.
Таблица 16. Расчет «ожидаемых» и стандартизированных показателей (III / IV этап)
IV этап — вычисление стандартизированных показателей. На этом этапе находим итог результатов, рассчитанных на предыдущем этапе по всем группами для соответствующих больниц. Сумма «ожидаемых» чисел и есть стандартизованные по срокам госпитализации показатели частоты летальности для обеих больниц. Они составляют: для больницы А — 19,6; для больницы Б — 18,2 случаев смертей на 100 госпитализированных больных.
Вывод. При условиях одинакового состава больных с острой кишечной непроходимостью по срокам госпитализации в обеих больницах уровень летальности был бы выше в больнице А. Высокий фактический уровень летальности в больнице Б, определенный на II этапе, можно объяснить большей частью госпитализированных больных в поздние сроки (свыше 24 часов от начала заболевания). Уровень летальности зависит от состава больных по срокам госпитализации в исследуемой больнице. Следовательно, алгоритм расчета стандартизированных показателей прямым методом можно изобразить в виде схемы - алгоритма (рис. 14).
Рис. 14. Алгоритм расчета стандартизированных показателей прямым методом
Таким образом, стандартизированный показатель демонстрирует, какой была бы заболеваемость (летальность, смертность, инвалидность) в сравниваемых контингентах, если бы их состав был однородным, то есть расхождения в составе контингентов были бы нивелируемыми.
Таким способом можно установить факт влияния любого фактора на упомянутые показатели и обнаружить причину изменений показателей, которые рассчитываются обычными методами. Вопросы для контроля: 1. В каких случаях используют стандартизированные показатели? 2. В чем заключается практическая значимость метода стандартизации? 3. Как проводится оценивание стандартизированных показателей?
Таблица 23.
3. Сопоставляем фактические и теоретические данные (их разницу|) с расчетом величины отклонения и учетом| его направления (знака) — таблица. 24.
Таблица 24.
4. Рассчитываем квадрат отклонения теоретических данных от фактических и средний квадрат отклонения на одну «ожидаемую» группу. Данный этап расчета имеет такой вид в связи с тем, что на основе фактических отклонений невозможно определить его суммарную величину, поскольку она равняется нулю. При возведении отклонений в квадрат определяем их параметры для каждой группы (р — р1)2. Учитывая разное число больных в исследуемых группах величина отклонений может быть разной, потому квадрат их делимо на число соответствующих наблюдений каждой группы — (р — р1)2 / р1. Проведя расчеты, определяем (р — р1)2 и (р — р1)2 / р1. (таблица 25).
Таблица 25.
5. Определяем X2— итог результатов последнего этапа расчетов. В нашем случае X2= 19,5.
n1= (S-| 1) (г-| 1), где S — число групп больных (для нашего примера |приклада| - три). г — число результативных групп (три). |Число степеней свободы n1= (3 - 1) (3 - 1) = 4.
Полученный результат превышает табличное значение X2 для n1 = 4 по всем уровням достоверности. Следовательно, мы можем сделать вывод о существенности (достоверность) разницы между показателями при разных методах лечения — «нулевая» гипотеза не подтвердилась. Вопросы для контроля: • В каких случаях целесообразно использовать параметрические критерии? • Какие преимущества имеют непараметрические критерии? • Какие непараметрические критерии используют для оценивания достоверности разности |разносрезультатов исследования во взаимосвязанных совокупностей? • Какие непараметрические критерии используют для оценки достоверности разности|разность| результатов исследования в независимой совокупности? Таблица 26.
Коэффициент парной корреляции отображает характер связи 2 признаков. Он может быть рассчитан при сопоставлении двух рядов в виде рангового коэффициента корреляции (ρ ) и линейного коэффициента корреляции (r).
Корреляционная зависимость различается по направлению, силе и форме связи (таблица 26). По направлению корреляционная связь может быть положительной ("прямой") и отрицательной ("обратной"). Степень, сила или теснота корреляционной связи определяется по величине коэффициента корреляции. Сила связи не зависит от ее направленности и определяется по абсолютному значению коэффициента корреляции.
Максимальное возможное абсолютное значение коэффициента корреляции r = 1,00; минимальное r = 0,00.
Коэффициент ранговой корреляции Спирмена - это непараметрический метод, который используется с целью статистического изучения связи между явлениями. Практический расчет коэффициента ранговой корреляции Спирмена включает следующие этапы: 1) Определить каждому из признаков их порядковый номер (ранг) по возрастанию (или убыванию). 2) Определить разности рангов каждой пары сопоставляемых значений. 3) Возвести в квадрат каждую разность и суммировать полученные результаты. 4) Вычислить коэффициент корреляции рангов по формуле:
ρ =1-
где
Методика расчета на примере характеристики взаимосвязи стажа работы работников угольной промышленности и частотой заболеваний на бронхит в них.
При большом числе наблюдений (n> 100) средняя погрешность рангового коэффициента корреляции может быть определена по формуле: mp=
Оценка достоверности коэффициента корреляции проводиться по тем же принципами, что используются для других показателей с учетом числа наблюдений (числа степеней свободы вариационных рядов n` = n – 2).
Один из методов расчета коэффициента линейной корреляции был предложен К.Пирсоном. Формула для подсчета коэффициента корреляции Пирсона такова: r = X и Y – варианты сравниваемых вариационных рядов; dx и dy – отклонение каждой варианты от своей средней арифметческой
Таблица 28. Зависимость между составом железа в крови и уровнем гемоглобина в крови.
Расчет линейного коэффициента корреляции: 1. Определяют средние значения для каждого ряда (Хх, Ху). 2. Определяют отклонение каждого из значений ряда от средней величины (dх, dу). 3. Возводят определенные отклонения в квадрат и определяют их суммы:
Достоверность полученного результата определим соотношением t = r / mr, где mr при малом числе наблюдений (n < 30) равняется: mr=
При большом числе наблюдений (n > 100) формула для расчета средней погрешности коэффициента корреляции может иметь вид: m=
Прямолинейная корреляционная связь между параметрами характеризуется тем, что каждому из одинаковых измерений одного показателя отвечает определено среднее значение другого показателя. Данную зависимость можно описать коэффициентом регрессии. Рассчитывается коэффициент регрессии по формуле: Rx/y=rxy* Где: Rx/y - коэффициент регрессии от Х до У; rxy - коэффициент корреляции;
Выше приведенные методики расчета парных коэффициентов корреляции являются основой и только первым этапом многофакторного корреляционной анализа. Парные коэффициенты показывают характер связи (общего, «неочищенного») между исследуемыми параметрами без учёта влияния других факторов. Оценивание «чистой» взаимосвязи в многофакторных моделях определяется на основе парциальных коэффициентов корреляции, основой для расчета которых являются парные и множественные коэффициенты. В практике медицинских исследований достаточно часто возникает вопрос об определении влияния нескольких разных факторов на определенное явление, например, на частоту осложнений при родах влияет возраст женщины, наличие акушерской и экстрагенитальной патологии, качество предоставления медицинской помощи и др. В таких случаях для выявления комбинированного влияния нескольких факторов на размер исследуемого явления пользуются методом множественной корреляции. Использование этого метода проводиться в несколько этапов. Математический аппарат данного анализа является достаточно сложным и выходит за пределы программы подготовки врачей. В настоящее время существует много специализированных программ статистического анализа, которые позволяют рассчитать множественный коэффициент корреляции для определенной совокупности показателей. Важным является оценка результата: в случае, когда сумма парциальных коэффициентов корреляции меньше величины множественного коэффициента корреляции, мы можем говорить о потенцируемом действии исследуемых параметров относительно результативного признака. Иначе (что, по нашему опыту, случается чаще) мы можем отмечать параллельное влияние факторов с невыраженным взаимным потенцируемым эффектом с условия, когда сумма парциальных коэффициентов значительно превышает значение множественного коэффициента корреляции. Следовательно, множественный коэффициент корреляции отображает связь одновременно комплекса факторов с исследуемым результативным фактором (клиническими показателями и др.). Вопросы для контроля: 1.Что такое корреляционная связь? Чем она отличается от функциональной? 2.Дайте характеристику формы, направления и силы связи. 3.Что такое регрессия?
СЛОВАРЬ
Абсолютно слепое (зашифрованное) исследование (total blind study) – исследование, в котором распределение субъектов из групп лечение неизвестно ни субъектам, ни исследователям, ни кому бы то ни было, кто непосредственно общается с исследователями, субъектами или имеет отношение к обработке данных (статистики и др.)
Абсолютное снижение риска (absolute risk reduction – ARR) – разница частоты неблагоприятных выходов между экспериментальной и контрольной группой.
Абсолютный (дополнительный, атрибутивный) риск (attributable risk) — это разница показателей заболеваемости или ее последствий у лиц, которые находятся или не находятся под воздействием исследуемого фактора. Дополнительный риск — это дополнительные случаи развития заболеваемости, предопределенные влиянием фактора риска. В зависимости от способа вычисления дополнительного риска, его также называют разницей рисков (difference risk), или непосредственным риском.
Анализ выживаемости (survival analysis) проводится в конце исследования у пациентов с высоким риском смертности. Необходимость проведения может возникнуть в кардиологических исследованиях для оценивания выживания после сердечного приступа.
Аналитическое исследование (analytic study) — тип эпидемиологического исследования, направленного на поиск причинных связей путем определения и измерения фактора риска или оценивания влияния определенных внешних влияний на здоровье. В аналитическом исследовании лица отбираются по наличию или отсутствию исследуемого заболевания или его предвестника, и для каждого из них устанавливаются личные характеристики (пол, возраст, профессия, но др.) и другие факторы риска, которые могут влиять на возникновение заболевания.
Асимметрия (skewness) — одна из характеристик формы распределения. У сдвинутого справа распределения значения группируются влево от среднего и образуют длинный хвост справа от него.
Многоцентровое исследование (multicenter study) — клиническое исследование, которое проведено в соответствии с единственным протоколом в нескольких исследовательских центрах несколькими исследователями.
База данных (database) — это сохраненные в электронном виде и особенным чином организованные (для облегчения поиска и доступа) данные.
Биостатистика (biostatistics) — раздел статистики, которая занимается обработкой результатов исследований в отрасли биологи и медицины.
Валидизация данных (validation of data) — процедуры, которые выполняются с целью гарантии, что данные окончательного клинического отчета отвечают оригинальным наблюдением.
Вариационный ряд (set of order statistics) — выборка, упорядоченная за значениями.
«Стоимость-выгода» (cost - benefit) — в денежном выражении оцениваются стоимость и результаты лечения. «Стоимость-эффективность» (cost - effectiveness) — в денежном выражении оценивается стоимость лечения, а результаты рассматриваются как выполнение определенных задач.
Верификация данных (verification of data) процедуры, направленные на выявление механических ошибок, которые возникают при перенесении данных из исходных документов в анкету и из анкеты в базу данных.
Открытое исследование (ореn study) — исследование, в котором разделение пациентов по группам лечения известен всем. Это может быть исследование, в котором изучается один или несколько видов лечения.
Относительный риск (relative risk) или отношение рисков (risk ratio) — это отношение показателя заболеваемости (или ее последствий) у лиц, которые подвергались влиянию исследуемого фактора, к величине показателя заболеваемости (или ее последствий) у лиц, которые не подпадали пицц влияние этого фактора. Относительный риск показывает силу связи между влиянием и заболеванием.
Воспроизводимость (reproducibility) — вероятность того, что при повторных измерениях определенной стойкого явления, сделанных разными людьми, на разных приборах, в разное время и в разных местах, будет получено одинаковый результат.
Генеральная совокупность (population) — это полная совокупность единиц наблюдения (людей), которые являются источником данных.
Гистограмма (hystogram) — это способ графического представления распределения числовых (непрерывных) данных, которое часто используют для иллюстрации основных характеристик распределения. Диапазон возможных значений переменной, делящийся на отрезки, которые задают разбивку выборки на классы, или группы. Каждой группе на гистограмме отвечает прямоугольник, длина которого равняется диапазону значений в заданной группе, а площадь пропорциональна числу наблюдений в этой группе.
Группирование (grouping) — переход к новой (иногда виртуальной) переменной. Ее градации определяют категории, которые являются объединением категорий объектов, которые отвечают градациям исходной переменной.
Данные выходные (source data) — вся информация, которая содержится в оригинальных записях и заверенных копиях оригинальных записей о клинических данных, наблюдениях или других мероприятиях, проведенных в ходе клинического исследования, необходимая для воссоздания хода исследования и для его оценки. Выходные данные содержатся в исходной документации (оригинальные записи и засвидетельствованные копии).
Дизайн исследования (design of a study) — способ, схема проведения исследования.
Доверительный интервал (confidence interval) — для параметра генеральной совокупности — это отрезок, что с большой вероятностью содержит этот параметр.
Доверительные пределы — нижний и верхний пределы доверительного интервала.
Доклиническое исследование (рге-clinical study) — биомедицинское исследование, что проведено без участия людей как субъектное исследования.
Исследование пилотное (pilot study) — иногда исследования проводят на незначительном количестве пациентов с целью определения, возможно ли провести исследование для большего числа пациентов. Это может быть очень полезно для выяснения тех трудностей, которые могут негативно повлиять на другое исследование. Другая цель проведения пилотного исследования заключается в том, чтобы получить информацию об отличии между двумя методами лечения, которое позволит установить количество пациентов, которые должны быть включены в основное исследование
Долгосрочное исследование (longterm trial) — исследование эффективности и безопасности препарата при долгосрочном лечении хронического заболевания, длительное наблюдение за пациентами по окончании проведенного лечения (при рецидиве опухоли после успешной химиотерапии) или хирургического вмешательства (выживаемость после трансплантации почки).
Исследование «случай-контроль» (саsе control stady, саsе-reference) — ретроспективное исследование, в котором по архивным данным или воспоминаниям, суждениям пациентов проводится сравнения двух групп, в одну из которых отобранные пациенты с определенной патологией, а в другую — без этой патологии.
Экстраполяция (extrapolation) — прогнозирование значения переменной за пределами интервала анализа. Срок применяется, как правило, при анализе динамических рядов для коротких промежутков времени.
Экспериментальные эпидемиологические исследования (experimental study) — это исследования, которые проводятся при непосредственном контроле со стороны исследователя за исследуемыми явлениями (например, за факторами риска, новыми методами лечения, диагностики или профилактики) в условиях, максимально приближенных к условиям лабораторного эксперимента.
Эмпирические, или обсервационное исследование (observational study) — это исследование без преднамеренного вмешательства в естественный ход и развитие заболевания.
Эпидемиология (epidemiology) — это изучение распространенности и детерминант состояний или событий, связанных со здоровьем, в специально определенных популяциях для управления и контроля по проблемам здоровья.
Заболеваемость (incidence rate) — частота новых случаев заболеваний в популяции, где этого заболевания сначала не было.
Cглаживание скользящими средними (moving average smoothing) — один из способов выравнивания динамического ряда.
Пе |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 816; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.153.240 (0.011 с.) |








 - сумма квадратов разностей рангов, а
- сумма квадратов разностей рангов, а  - число парных наблюдений.
- число парных наблюдений.
 =1-6*2/5*(25-1)=
=1-6*2/5*(25-1)= 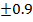 ВЫВОД: между стажем работы работников и частотой заболевания на бронхит выявлено сильную, прямую корреляционную связь.
Ошибка рангового коэффициента корреляции для нашего случая исчисляется по формуле:
m=
ВЫВОД: между стажем работы работников и частотой заболевания на бронхит выявлено сильную, прямую корреляционную связь.
Ошибка рангового коэффициента корреляции для нашего случая исчисляется по формуле:
m=  для нашего случая m1=0,245 и t=3,67, что, соответственно, выше граничных значений. Полученный результат позволяет сделать вывод о вероятности данного рангового коэффициента корреляции.
для нашего случая m1=0,245 и t=3,67, что, соответственно, выше граничных значений. Полученный результат позволяет сделать вывод о вероятности данного рангового коэффициента корреляции.









 =34.89
=34.89
 Вывод: между составом железа в крови и уровнем гемоглобина существует сильная прямая связь. Для нашего случая коэффициент вероятности=3,6, что свыше гранично допустимых значений при вероятности ошибки меньшей 0,05
Вывод: между составом железа в крови и уровнем гемоглобина существует сильная прямая связь. Для нашего случая коэффициент вероятности=3,6, что свыше гранично допустимых значений при вероятности ошибки меньшей 0,05




 и
и  средние квадратические отклонения рядов Х и У.
средние квадратические отклонения рядов Х и У. Х = 3,2 см и Ху = 30,7 кг;
Х = 3,2 см и Ху = 30,7 кг;  (кг)
Вывод: при изменении роста на 1 см вес мальчиков в среднем изменится на 1,47 кг. Определенный коэффициент регрессии можно использовать в уравнении регрессии при прогнозировании ситуации - какой вес в среднем будет отвечать возрасту мальчиков 140,0 см:
Вывод: возрасту мальчиков 140,0 см будет отвечать вес 34,8 кг.
(кг)
Вывод: при изменении роста на 1 см вес мальчиков в среднем изменится на 1,47 кг. Определенный коэффициент регрессии можно использовать в уравнении регрессии при прогнозировании ситуации - какой вес в среднем будет отвечать возрасту мальчиков 140,0 см:
Вывод: возрасту мальчиков 140,0 см будет отвечать вес 34,8 кг.



