
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типовые задачи анализа данныхСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Введение Настоящий выпуск является вторым из серии выпусков, в которых излагается курс «Математическое моделирование геологических объектов», сопровождаемый учебно-методическими рекомендациями, контрольными вопросами и комментариями. В этом выпуске первоочередное внимание уделяется анализу данных как самостоятельной научной дисциплине и в его сопряжении с прикладной статистикой. Излагается, конечно, не «весь» анализ данных, а только отдельные его фрагменты, необходимые для понимания курса в целом. Приводятся минимально необходимые сведения о прикладной статистике. Математическое моделирование геологических объектов тесно связано с анализом данных, как самостоятельной научной дисциплиной, и прикладной статистикой. Каким образом анализ данных, математическое моделирование и прикладная статистика совместно используются при решении конкретных геологических задач и, в частности, при создании моделей геологических объектов? Обычно создание модели геологического объекта разбивается на ряд подзадач, образующих единую блок-схему с последовательным и параллельным движением обрабатываемой информации от исходных процедур к конечному результату – синтезу модели. Решение каждой из таких подзадач сводится либо к построению и анализу некоторой частной модели, либо к поиску стохастической зависимости между некоторыми параметрами, либо к решению той или иной типовой задачи анализа данных и т.п. В последнем случае выбирается алгоритм, удовлетворяющий требованиям, предъявляемым исходной информацией. Требования эти могут иметь как чисто формальный характер (например, наличие в таблице разнотипных признаков делает невозможным применение некоторых алгоритмов), так и представлять собой «трудно» формализуемые представления о системе исследуемых объектов, которыми тоже не следует пренебрегать. В настоящее время не существует универсального формально-математического способа для выбора подходящего алгоритма. Поэтому при выборе алгоритма наряду с проверкой его формально-математической пригодности рекомендуется ориентироваться и на его относительную простоту и содержательную интерпретируемость используемого математического аппарата в конкретной задаче, опыт применения алгоритма при решении аналогичных задач.
Распознавание образов Основные подзадачи Основными подзадачами задачи распознавания являются: 1) создание исходного списка признаков; 2) выбор классов объектов; 3) подготовка таблицы (таблиц) обучения; 4) выбор семейства решающих правил; 5) поиск оптимального (относительно некоторого критерия или критериев) решающего правила в этом семействе; 6) подготовка описаний проб; 7) распознавание проб. На этапах 1 - 3 производится выбор и экспликация признаков (см. пособие Красавчикова, 2008) и составление базы данных. При создании исходного перечня признаков могут быть реализованы два подхода: А) всестороннее описание объектов, характерное для ситуаций, когда исследователь не знает, из каких признаков должен быть составлен окончательный список (информативная система признаков), по которому будет производиться распознавание проб. Поэтому он отбирает такие признаки, которые, в принципе, могут содержать полезную информацию (хотя, на первый взгляд, их связь с решаемой задачей может быть и не очевидна), и полагается в выборе информативной системы признаков на алгоритм и реализующую его программу. Б) описание объектов, основанное на некоторой геологической модели, для которой список признаков заранее известен. При выборе классов объектов исходят не только из постановки задачи (например, разбраковать локальные поднятия на перспективные и бесперспективные по результатам интерпретации данных сейсморазведки), но и основываются на геологическом смысле и опыте решения аналогичных задач. Возможно, придётся проводить декомпозицию задачи и осуществлять поэтапное решение в рамках последовательно-параллельной блок-схемы несколько задач распознавания. При подготовке таблицы (таблиц) обучения следует, по-возможности, избегать появления характеристических признаков, замеренных в шкале наименований (номинальных) с числом принимаемых ими значений, превосходящим два, поскольку они резко ограничивают выбор алгоритма распознавания. Они могут содержать весьма существенную информацию, но лучше, чтобы они не входили в список характеристических признаков. Обычно, по значениям таких признаков формируются классы.
Выбор семейства решающих правил не является формальной процедурой. Однако, при этом выборе есть и формальные требования. Например, если среди признаков есть номинальные или ранговые, то можно использовать только те алгоритмы, которые способны работать с информацией, представленной в качественных шкалах. Одним из главных критериев выбора решающего правила является его «простота». Практика показала, что предпочтение следует отдавать более простым решающим правилам. Если среди «простых» решающих правил (причём, доступных исследователю в программной реализации) не удаётся найти способного справиться с поставленной задачей (или, в случае (а), радикально сократить размерность описания), то переходят к более сложным и т.д. Формализовать понятие простоты не так-то просто! В математической логике и теории алгоритмов есть целое направление, связанное с формализацией и изучением простоты математических конструкций, но знакомство с этой тематикой не входит в задачи курса. Поэтому будем относиться к этой проблематике как интуитивно ясной. По всей видимости, примером наиболее простых решающих правил могут служить линейные (см. ниже). Если есть два линейных решающих правила, то более простым, очевидно, является то, которое использует меньшее число признаков. В случае (а) при выборе семейства решающих правил следует обращать особое внимание на способность радикального сокращения размерности описания. После выбора семейства проводится поиск решающей функции и соответствующего правила, которые в этом семействе обладают «наилучшим качеством» по отношению к материалу обучения и экзамена. Для оценки качества решающего правила используются функционалы наподобие нижеприведённого: Δ(F,λ,ε)=p1M1 + p2M2 +p3M3 + p4M4, где для материала обучения и экзамена M1 – число ошибочно распознанных объектов первого класса; M2 – число ошибочно распознанных объектов второго класса; M3 – число отказов для объектов первого класса; M4 – число отказов для объектов второго класса. Коэффициенты pj, j=1,…,4, – «штрафы» за ошибку соответствующего типа. Чем меньше значение Δ(F,λ,ε) (при фиксированных списках объектов обучения и экзамена), тем выше качество решающего правила. После того, как для всех объектов обучения и экзамена вычислены значения решающей функции, управляющие параметры алгоритма λ, ε могут быть выбраны оптимальным образом, т.е. так, чтобы функционал качества решающего правила достигал минимума: Δ(F,λ*,ε*)=min Δ(F,λ,ε), где минимум берётся по всемλ, ε и ε>0. В случае (а) ещё одним (и не менее важным) критерием качества является резко сокращение числа признаков, используемых в распознавании, по сравнению с исходным списком. Это обусловлено тем, что - малое число признаков уменьшает влияние «информационных шумов», что делает распознавание более надёжным; - сокращается время на подготовку описаний проб. Так, при распознавании в узлах сеток уменьшается число карт, которые приходится строить; - появляется возможность содержательно проинтерпретировать решающее правило и т.д. Описание проб производится по признакам, используемым в оптимальном решающем правиле. В случае (а) это особенно важно, т.к., в частности, существенно сокращается время на подготовку описаний.
Примеры алгоритмов распознавания К настоящему времени опубликованы сотни методов распознавания. Они объединяются в семейства. Зачастую, эти семейства описываются в виде решающих функций (либо правил) с неопределёнными параметрами. Устоявшейся общепризнанной классификации семейств алгоритмов распознавания не существует. Поэтому ограничимся кратким описанием нескольких семейств алгоритмов, показавших свою эффективность при решении прикладных геологических задач, особенно в геологии нефти и газа. Для подробного ознакомления с применением методов распознавания в геологии нефти и газа отсылаем читателя к публикациям 60-80 годов прошлого века, когда их использование при решения задач прогнозно-поискового профиля было массовым. Методы распознавания применялись, в частности, при решении задач прогноза гигантских нефтяных месторождений, продуктивности локальных поднятий, фазового состояния УВ в залежах и др. (Распознавание образов…, 1971; Раздельное прогнозирование…, 1978, Прогноз месторождений …, 1981 и др.).
4.3.1. Байесовские решающие правила Эти решающие правила подробно охарактеризованы в учебном пособии Дёмина (2005), куда мы и отсылаем читателя. Для более глубокого ознакомления с приложениями байесовской теории принятия решений в геологии нефти и газа рекомендуем обратиться к монографии (Прогноз месторождений…, 1981).
4.3.2. Комбинаторно-логические методы в распознавании Применение этих методов рассмотрим на примере одной конкретной схемы распознавания, основанной на аппарате дискретной математики и математической логики. Пусть сначала для простоты изложения все признаки X1,…,Xn – бинарные. Согласно Журавлёву (1978) назовём произвольную совокупность W наборов признаков вида w=(Xj(1),…,Xj(k)), где k=1,…,n, системой опорных множеств, W={w1, w2,…, wN}, а её элементы wr – опорными множествами. Пусть wÎW, w=(Xj(1),…,Xj(L)), Sk – строка таблицы Определение 1. Набор признаков wÎW голосует за отнесение строки S к первому классу, если в таблице T1 найдётся строка Sk, такая, что по набору w строки S и Sk не различаются; w голосует за отнесение строки S ко второму классу, если в таблице T2 найдётся строка Qp, такая, что по набору w строки S и Qp не различаются. Пусть Г1(S), Г2(S) – числа голосов по всем wÎW за отнесение строки S к первому и второму классам соответственно. Тогда решающее правило имеет вид:
при Г1(S) >
при Г2(S) > в остальных случаях S не распознаётся.
Смысл этого решающего правила заключается в том, что для отнесения пробы S к классу Kj, где j=1,2, она должна получить – больше голосов за класс Kj, чем любой объект противоположного класса; – не больше голосов за противоположный класс, чем самый близкий к этому классу объект обучения класса Kj. Близость здесь оценивается числом голосов за класс. Эта схема представляет собой один из простейших вариантов голосования по системе опорных множеств. Алгоритм представляет собой реализацию так называемого «принципа частичной прецедентности» (Журавлёв, 1978), при котором заключение о принадлежности объекта к классу выносится на основе анализа совпадений фрагментов его описания с соответствующими фрагментами описаний объектов этого класса. Совпадение фрагментов описаний объекта обучения и пробы является частичным прецедентом. Пример системы опорных множеств: тестовая конструкция. Её основой являются понятия теста и тупикового теста, предложенные С.В. Яблонским в качестве математического аппарата диагностики технических устройств (Журавлёв, 1978). Определение 2. Набор столбцовw называется тестом для пары таблиц T1, T2 если по нему нет совпадений между строками Si и Qp, где Определение 3. Тест называется тупиковым, если из него нельзя удалить ни одного столбца без того, чтобы он перестал быть тестом. Дмитриев, Журавлёв, Кренделев (1966) воспользовались аппаратом тупиковых тестов для создания алгоритмов классификации предметов и явлений. В геологии нефти и газа комбинаторно-логические методы впервые были применены при решении задач прогноза гигантских нефтяных месторождений (Распознавание образов …, 1971), где была использована тестовая конструкция. Под руководством А.А. Трофимука тестовый подход применён также и к решению других важнейших прогнозных задач геологии нефти и газа (Раздельное прогнозирование…, 1978 и др.). Ряд сделанных А.А. Трофимуком прогнозов, не нашедших поддержки в момент опубликования, в дальнейшем блестяще подтвердились. Константиновым, Королёвой, Кудрявцевым (1976) на представительном фактическом материале по прогнозу рудоносности была подтверждена эффективность алгоритмов тестового подхода по сравнению с другими алгоритмами распознавания, применявшимися для решения задач рудопрогноза. В геологии нефти и газа другие системы опорных множеств не применялись. Если в таблицах встречаются признаки, замеренные в количественных шкалах, то для них используются пороговые меры различимости значений (см. Красавчиков, 2009). 4.3.1. Линейные методы Линейные методы стали применяться для решения задач распознавания образов одними из первых (см.. Ту, Гонсалес, 1978) в середине прошлого века. Пусть F(u1,…,un)=a1u1 + a2u2 + … +anun – линейная функция n переменных u1,…,un. Методы отыскания линейных решающих функций и правил принято называть линейными. Общий вид линейных решающих правил может быть задан следующим образом:
при a1X1(S) + a2X2(S) + … +anXn(S)≥λ+ε объект S относится к К1; при a1X1(S) + a2X2(S) + … +anXn(S)≤λ-ε объект S относится к К2; при λ-ε <a1X1(S) + a2X2(S) + … +anXn(S)<λ+ε объект S не распознаётся. Пусть
где j=1,…,n, i=1,…,m(1), k=m(1)+1,…,m c неизвестными y1,…,yn (искомыми значениями коэффициентов aj) и λ. Для проверки существования решения систем линейных неравенств используются вычислительные методы линейной алгебры; эта проверка является «не слишком сложной», а программное обеспечение содержится в общераспространённых пакетах. Если решение существует, то оно либо единственно, либо их бесконечно много. Существуют многочисленные методы нахождения линейных решающих правил, реализующие различные дополнительные требования (типа максимизации ε, сокращения размерности описания и пр.). Геометрическая интерпретация линейного решающего правила заключается в следующем. Пусть все признаки замерены в количественных шкалах и En – n-мерное евклидово пространство. Гиперплоскость a1 x 1+a2 x 2+…+an x n= λ делит En на две части таким образом, что в каждой из них находятся точки только одного из классов. Такие гиперплоскости называются разделяющими. Ситуация заметно усложняется, если разделяющей гиперплоскости не существует и нужно отыскать гиперплоскость, минимизирующую функционал качества распознавания. С вычислительной точки зрения эта задача является намного более сложной. Линейные методы распознавания использовались в течение ряда лет для прогноза продуктивности локальных поднятий и уточнения границ природных резервуаров УВ в нижне -среднеюрских отложениях Западной Сибири (Каштанов, Соколов, 1976, Красавчиков, 2007).
Упорядочение На практике вместо отыскания решающей функции, удовлетворяющей цепочке неравенств (1), зачастую достаточно получить «хорошую» корреляцию упорядочения по убыванию значений функции F с упорядочением на материале обучения. Это имеет принципиальное значение, поскольку решающей функции, для которой выполняются неравенства (1), в классах «простых» функций (типа линейных и т.п.) может и не существовать. Для приближённого решения этой задачи можно применять математический аппарат множественной линейной регрессии, реализованный в программном продукте Statistica for Windows. Пусть приближённое решение F ищется в классе линейных функций, F(u1,u2,…,un)= a 1u1+ a2 u2+…+ an un+ b, где a 1,…, a n, b – коэффициенты при переменных и свободный член соответственно, Ψ – некоторая монотонная функция, определённая на множестве значений целевого признака (например, логарифм, см. пояснение в разделе 10). Тогда, решая задачу множественной линейной регрессии вида: найти a 1,…, a n, b, при которых функционал
достигает минимума, мы получаем приближённое решение задачи упорядочения через аппроксимацию некоторой монотонной функции от целевого признака. Поскольку функция Ψ монотонна, можно, используя коэффициент Спирмена, оценить достоверность связи между решением регрессионной задачи и значениями целевого признака X n+1. Значение rs является естественным показателем качества приближённого решения задачи упорядочения. Можно показать, что для отыскания точного решения F в классе линейных решающих функций достаточно решить систему m-1 нестрогих линейных неравенств c n неизвестными p 1,…, p n:
где n – число признаков, e>0 – малая положительная константа. При этом, как легко видеть, разности Xj(Si) - Xj(Si+1)=Hij являются известными величинами. Обратно, из существования решения системы линейных неравенств (3) вытекает существование решения системы неравенств (2). Однако, как уже отмечалось, в классе линейных решающих функций решения может и не существовать. Программное обеспечение для решения систем нестрогих линейных неравенств отсутствует в пакете Statistica. Однако оно, в принципе, является достаточно распространённым и содержится в программных продуктах, предназначенных для решения задач вычислительной алгебры.
Кластер-анализ Существует большое количество методов и алгоритмов кластер анализа. Среди них выделяются две крупные группы, к которым относится большинство опубликованных алгоритмов. Это иерархические алгоритмы, порождающие древовидные классификации объектов, и алгоритмы, порождающие разбиения (группировки).
Иерархические алгоритмы Среди иерархических алгоритмов можно выделить два основных класса – агломеративные и дивизимные. Это – пошаговые алгоритмы. Агломеративные алгоритмы начинают с того, что каждый объект является отдельным кластером, а заканчивают тем, что все кластеры объединяются в один объект. На каждом шаге производится объединение двух наиболее «близких» в некотором смысле кластеров. Близость между кластерами задаётся «расстоянием» либо мерой близости. Под «расстоянием» в данном случае понимается неотрицательная симметричная функция. Примеры таких функций будут рассмотрены ниже. В дивизимных же методах, наоборот, на первом шаге все объекты образуют один кластер, на последнем – каждый объект представляет отдельный кластер.
6.1.1. Агломеративные алгоритмы Рассмотрим агломеративные методы, представленные в пакете Statistica for Windows. Для этого сначала определим функции, с помощью которых оцениваются расстояния между конечными подмножествами метрического пространства M. Пусть множество описаний объектов S= {S1,…,Sm} признаками X1(S),…,Xn(S) содержится в евклидовом пространстве En, так что для любой пары объектов Si, Sj из S определена метрика (расстояние) ρij= ρ(Si,Sj) и можно составить симметричную матрицу расстояний R=(ρij)m´m. Приведём примеры функций двух переменных, значения которых играют в кластер-анализе роль расстояний между непересекающимися подмножествами, хотя, формально, эти функции не являются метриками. Пусть Al, Aq Ì S неимеют общих элементов, AlÇAq = Æ. Тогда: а) ρlq равно расстоянию между двумя ближайшими объектами множеств Al, Aq;. б) ρlq равно расстоянию между самыми далекими объектами множеств Al, Aq; в) ρlq равно расстоянию между центрами тяжести множеств Al, Aq (точек со средними значениями всех показателей); г) ρlq равно среднему арифметическому расстояний между объектами множеств Al, Aq; д) ρlq равно расстоянию между точками с медианными значениями признаков для мно- жеств Al, Aq; е) ρlq равно сумме расстояний между элементами множеств Al, Aq. ж) ρlq равно так называемому «статистическому расстоянию» (Дюран, Оделл, 1977) между множествами Al, Aq:
Здесь В иерархических агломеративных алгоритмах, основанных на вычислении «расстояний» между подмножествами Al, Aq вида (а-ж) и им подобных, на первом шаге каждый объект считается отдельным кластером. На следующем шаге объединяются два ближайших объекта, которые образуют новый класс, определяются «расстояния» от этого класса до всех остальных объектов. Матрица расстояний, соответственно, изменяется с учётом результатов кластеризации, включая уменьшение её размерности. На р-м шаге для кластеров и матрицы расстояний предыдущего шага Rp-1 повторяется та же процедура, пока все объекты не объединятся в один кластер. В отличие от R1=R, при p>1 элементами Rp являются не расстояния между объектами, а «расстояния» между кластерами. Если сразу несколько объектов (либо кластеров) имеют минимальное «расстояние», то возможны две стратегии: выбрать одну случайную пару или объединить сразу все пары. Первый способ является классическим; иногда в литературе его называют восходящей иерархической классификацией. Второй способ используется гораздо реже. Метод, основанный на вычислении «статистического расстояния» (см. п. (ж) выше) называется методом Уорда (Мандель, 1988) по имени предложившего его специалиста. Названия остальных методов определяются используемым в них расстоянием. Результаты работы всех иерархических агломеративных процедур обычно оформляются в виде так называемой дендрограммы (см. рис. 1), в которой по горизонтали показаны номера объектов, а по вертикали – значения межкластерных расстояний ρlq, при которых произошло объединение двух кластеров.
6.1.2. Дивизимные алгоритмы Этот класс алгоритмов кластер-анализа опишем на примере «Быстрого дивизимного комбинационного алгоритма», предложенного Chaudhuri (Мандель, 1988). Проведённые в ИНГГ эксперименты показали его высокую эффективность при решении задачи кластеризации разрезов по толщинам составляющих их горизонтов на основе информации, содержащейся в сетках толщин. Обработка информации по средней юре юго-востока ЗСП показала, что он быстро и «разумно» кластеризует огромные массивы данных, представленных сеточными моделями. Другими алгоритмами кластеризовать эти массивы, состоящие, порой, из миллиона с лишним объектов, охарактеризованных более чем 10 признаками, часто невозможно либо крайне затруднительно. Алгоритм Chaudhuri (Чаудури) в программном продукте “Statistica for Windows” не представлен. Этот алгоритм для краткости будем называть также алгоритмом гиперкубов. Приведём его краткое описание. Гиперкуб, в котором содержатся все точки (определяемый размахами вариации признаков), разбивается на первом шаге по каждой оси перпендикулярной ей плоскостью на 2 n «кубика», где n –число признаков. На j -м шаге каждый из этих кубиков также разбивается, т. е. получается 2 n j гиперкуба. Если в полученном кубе есть хоть один объект, он считается заполненным, если нет – пустым. Кластером здесь называется максимально большая связная область, в которой любые два объекта соединены непустыми клетками (т.е. компонента связности графа, вершинами которого являются объекты, и две вершины в котором соединены ребром если и только если они либо находятся в одной клетке либо вмещающие их клетки имеют общую границу, пусть даже состоящую из одной точки). По мере увеличения j число кластеров растет, т.е. алгоритм носит дивизимный характер. Он принадлежит к числу наиболее быстрых иерархических алгоритмов, не требует предварительной нормировки показателей, хранения и пересчёта матрицы расстояний, может работать в исходном пространстве. Эти и некоторые другие особенности относят его к числу наиболее предпочтительных алгоритмов для построения иерархических классификаций в случае больших баз данных.
Раздел 2 1. Решающая функция в распознавании образов – это отображение, переводящее набор значений разнотипных признаков X1(S),…,Xn(S) в число. Это число – значение решающей функции F на объекте S. Решающее правило в распознавании образов – это высказывание, которое содержит значения решающей функции и управляющих параметров и, с учётом этих значений, либо относит пробу к одному из классов, либо отказывается от распознавания. 2. Сформулируйте понятие решающей функции применительно к задаче упорядочения. 3. Может ли целевой признак применительно к сформулированной в разделе 2 версии задачи упорядочения быть а) логическим; б) номинальным? 4. Почему на начальных этапах развития кластер - анализа его (в противовес распознаванию образов) называли «обучением без учителя»? 5. Зависимость между признаками может быть представлена как в виде, разрешённом относительно того или иного признака, например, Xj ≈ f(Xi,Xk,…,Xl), так и без такого разрешения. Например, (ln(Xj))2 + ln(Xj+Xk) -1≈0. 6. Сформулируйте задачу распознавания как задачу заполнения единичного пропуска. 7. Сформулируйте задачу заполнения единичного пропуска в бинарном или номинальном признаке как задачу распознавания. Раздел 3 1. В каких случаях и почему для оценки связи между количественными признаками рационально использовать ранговый коэффициент Спирмена? 2. Всегда ли множественная линейная регрессия будет точно решать задачу упорядочения? 3. Можно ли применять линейную регрессионную модель из раздела 3, если Y- ранговый признак? 4. Можно ли применять линейную регрессионную модель из раздела 3, если Y- номинальный признак? 5. Можно ли применять линейную регрессионную модель из раздела 3, если хотя бы один признак из списка X1,…,Xn – ранговый или номинальный? 6. Можно ли без предварительной нормировки признаков сопоставлять веса, с которыми они входят в уравнение регрессии, с целью их упорядочения по влиянию на значение прогнозируемого показателя? 7. Что такое b в разделе «Множественная линейная регрессия» пакета “Statistica for Windows? Как величины bj могут быть использованы при сравнении характеристических признаков по их влиянию на значение зависимого (целевого) признака?
Раздел 4 1. В чём заключается экспликация на этапе формирования списка исходных признаков? 2. Каким образом штрафы за ошибки и отказы позволяют регулировать оценку качества распознавания? 3. Какое из двух линейных решающих правил, имеющих одинаковую оценку качества распознавания, предпочтительнее: использующее 5 признаков или 7? 4. Если метод распознавания используется для уточнения границ (по латерали) геологического объекта в осадочной толще, то некоторый процент отказов или даже ошибок в узлах сетки может и не повлиять на прогнозируемое расположение его границы. В результате решения задачи распознавания образов для узлов сетки на принадлежность локального участка (центром которого является узел) к моделируемому объекту появляется предварительная версия границы. Обычно, в результате анализа полученной версии, геологическая ситуация, в целом, становится ясной, так что исследователь уже в состоянии «самостоятельно» провести границу объекта. 5. В результате решения задач распознавания с использованием признаков, рассчитанных по сеткам реперных геофизических поверхностей и данным глубокого бурения (разбивки по стратиграфическим уровням, толщины горизонтов и пр.), в ИНГГ СО РАН были уточнены границы (по латерали) основных стратиграфических горизонтов в нижне-среднеюрских отложениях Западной Сибири, что, в свою очередь, позволило уточнить оценки ресурсов УВ юры ряда крупных регионов. 6. Читая работы по применению методов распознавания в геологии нефти и газа, следует иметь в виду, что, обычно, исследователь опирается на свой опыт решения аналогичных задач и литературные данные; при этом использует не «самое лучшее» программное обеспечение, а то, которым располагает и умеет пользоваться. 7. Опыт решения многочисленных практических задач в области моделирования геологических объектов в слоистой толще позволяет сформулировать нижеследующие требования к алгоритмам и программному обеспечению распознавания образов применительно к моделированию региональных, зональных и локальных объектов в осадочном бассейне: - «уметь» работать с признаками, заданными на сетках; - отыскивать простые и легко интерпретируемые решающие правила; - обеспечивать эффективное снижение размерности описания n; - работать с зависимыми и разнотипными признаками; - учитывать сложный характер разделения классов (по латерали).
Раздел 5 Множественный линейный регрессионный анализ предназначен для отыскания линейной зависимости признака Y от признаков X1,…,Xn Y≈ a 1X1 +…+ anXn + b =L(X1,..., Xn). (4) В задаче упорядочения требуется решить более общую задачу: отыскать зависимость F, которая расставляет объекты обучения в порядке по убыванию значений целевого признака Xn+1. При этом может оказаться так, что значения функции F у объектов обучения и проб не будут совпадать со значениями целевого признака. Решение линейной регрессионной задачи по нахождению минимума функционала (4) может не привести к нахождению приемлемой аппроксимации решения задачи упорядочения. Однако, можно попытаться провести преобразование целевого признака Xn+1 монотонной функцией Ψ таким образом, чтобы для Ψ(Xn+1) методом наименьших квадратов можно было получить искомую аппроксимацию. Поскольку Ψ монотонна, это даёт решение задачи упорядочения. «Универсального» способа выбора Ψ, скорее всего, не существует. Однако можно привести некоторые практические рекомендации по его подбору. Монотонная функция Ψ, как правило, используется в том случае, когда «обычный» коэффициент парной корреляции r (Дёмин, 2005, с. 42-44) между значениями целевого признака Xn+1 и соответствующими значениями, рассчитанными по уравнению множественной линейной регрессии, «мал». При этом содержательные соображения позволяют предполагать, что упорядочить объекты по убыванию целевого признака Xn+1 по значениям X1,..., Xn всё-таки можно. Чаще всего множественная линейная регрессия с «удачно подобранным» Ψ успешно применяется, когда распределение значений в последовательности Xn+1(Sm), Xn+1(Sm-1),…, Xn+1(S1) имеет ярко выраженный нелинейный характер, сопоставимый, например, с экспонентой. Функция Ψ, обычно, выбирается таким образом, чтобы, по возможности, устранить резкую нелинейность. Логарифм – типичный пример подобной функции, неоднократно использованный в подобных ситуациях при решении практических задач Раздел 6 1.Пусть Al={(0,1), (2,0), (2,3)}, Aq={(5,1), (6,2), (8,3), (9,5), (10,7)}. Рассчитайте расстояния (а –ж). 2. Полагая S= Al ÈAq решите задачу кластеризации совокупности объектов S методом Чоудари 3. На локальном уровне для отдельной площади или скопления площадей («малой» зоны) кластер-анализ успешно применяется при корреляции дизъюнктивных нарушений по данным 3D-сейсморазведки (Кашик и др, 2004). Опыт применения кластер-анализа на региональном и зональном уровне показал, что эти методы могут давать полезную информацию об истории развития изучаемых толщ и тектонических процессах, типах геологических разрезов, их раcпространении по латерали, зонах развития коллекторов в них, нефтегазоносности. Однако для этого, как выяснилось, нужны достаточно «густые» регулярные сетки толщин отложений, поэтому главный фактор, сдерживающий его применение при региональных и зональных построениях (в случае «больших» территорий), – необходимость хранения и пересчётов матрицы расстояний для всей совокупности объектов. Если исходить из оценки трудоёмкости вычислений, то на локальном уровне, за исключением обработки данных 3D-cейсморазведки, вполне можно использовать практически любые алгоритмы кластер-анализа. При региональных и зональных построениях с использованием сеточных моделей (в случае «больших» территорий), а также при обработке данных 3D-сейсморазведки (даже на уровне отдельной площади или «малой зоны»), целесообразно выбирать алгоритм, не требующий пересчёта матрицы расстояний, например, метод Чоудари. 4. Наметим, в общих чертах, подход, позволяющий эффективно использовать кластер-анализ данных бурения при прогнозных построениях. Пусть, например, анализируются данные по какому-либо региональному или зональному резервуару УВ. На основании некоторого исходного списка признаков (не включающего результаты испытаний скважин и их координаты) производится кластеризация объектов. Затем для каждого кластера анализируются пространственное размещение скважин и результаты их испытаний. У найденных кластеров вычисляются такие простые, но весьма информативные параметры как частость получения притока среди всех испытани
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 1773; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.108.80 (0.022 с.) |

 , Qp – строка таблицы
, Qp – строка таблицы  . Строки Sk и Qp различаются по набору признаков w, если найдётся входящий в w признак Xj(r) такой, что Xj(r)(Sk)¹Xj(r)(Qp). В противном случае будем говорить, что они не различаются.
. Строки Sk и Qp различаются по набору признаков w, если найдётся входящий в w признак Xj(r) такой, что Xj(r)(Sk)¹Xj(r)(Qp). В противном случае будем говорить, что они не различаются. Qp) и Г2(S) ≤
Qp) и Г2(S) ≤ 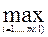 Г2(Si) объект S относится к классу K1;
Г2(Si) объект S относится к классу K1; Si) и Г1(S) ≤
Si) и Г1(S) ≤  Г1(Qp) объект S относится к классу K2;
Г1(Qp) объект S относится к классу K2; ,
, 

 , i=1,…,m-1, (3)
, i=1,…,m-1, (3) .
. – векторы средних значений признаков для подмножеств Al, Aq, T – знак транспонирования. Таким образом, «статистическое расстояние» между подмножествами Al, Aq представляет собой квадрат расстояния между векторами средних значений признаков (центрами тяжести)
– векторы средних значений признаков для подмножеств Al, Aq, T – знак транспонирования. Таким образом, «статистическое расстояние» между подмножествами Al, Aq представляет собой квадрат расстояния между векторами средних значений признаков (центрами тяжести) 


