
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы прикладной статистики в анализе данныхСодержание книги Поиск на нашем сайте
I. Пусть для объектов S1,…,Sm известны значения количественных признаков Y, X1,…,Xn, равные y = a 1 x 1 + …+an xn + b требуется найти значения a 1,…, a n, b, на которых достигает минимума функционал
Эти n+ 1 неизвестных отыскиваются методом наименьших квадратов (см. Дрейпер, Смит, 1973; Дёмин, 2005). II. Коэффициент ранговой корреляции Спирмена – мера зависимости двух признаков X и Y, основанная на ранжировании независимых результатов наблюдений (X1,Y1), …, (Xm,Ym), см. (Справочник…, 1990). Пусть, для простоты изложения, значения признаков X и Y в последовательности (X1,Y1),…,(Xm,Ym) не повторяются, как не повторяются и ранги, которые, в рассматриваемом случае представляют собой номера значений признаков X и Y в их упорядочениях по возрастанию, которые мы будем обозначать через rank(Xi) и rank(Yi), i=1, …,m, соответственно. Тогда коэффициент ранговой корреляции Спирмена определяется формулой
где d i – разность между рангами Xi и Yi, d i=rank(Xi) – rank(Yi). Если значения X или Y в этой последовательности повторяются, то формула усложняется за счёт учёта повторяющихся значений. Однако, если повторяющихся значений «не слишком много», то их влияние на значение rs пренебрежительно мал о. Коэффициент имеет следующее свойство: -1≤ rs ≤1. Мы получаем значения около +1, если б о льшим значениям признака X отвечают б о льшие значения признака Y, и значения около -1, если б о льшие значения X отвечают меньшим значениям Y. Оценка достоверности связи по уровню значимости (p-level) для rs является корректной без принятия допущений о виде функций распределения. В этом заключается главное преимущество rs по сравнению с «обычным» выборочным коэффициентом парной корреляции Пирсона r (Дёмин, 2005, с. 42-45). Дело в том, что для r уровень значимости (p-level)свидетельствует о достоверности (либо недостоверности) связи признаков X и Y только при выполнении достаточно жестких вероятностно-статистических предположений (например, при их совместном двухмерном нормальном распределении). III. В практике анализа данных значительную роль играют гистограммы эмпирического распределения значений признака X(S) на множестве объектов S1,…,Sm. Гистограммы рассматривались в курсе теории вероятностей и математической статистики. Поэтому напомним только, что не существует математически обоснованного способа выбора на гистограмме числа интервалов k(m), где m – число объектов, однако, при выборе k(m) зачастую руководствуются логарифмической формулой Стерджеса (Вероятность …, 1999): k(m)≈1+log2m. Пусть k определяется по формуле Стерджеса. Тогда длина интервала на гистограмме равняется (xmax-x min)/k(m), где xmin, xmax – минимальное и максимальное значения признака X на множестве объектов S1,…,Sm. Упомянутый в разделе 3 математический аппарат (кроме формулы Стерджеса) реализован в программном продукте Statistica for Windows (см. о нём в книге Боровикова В.П., Боровикова И.П. (1997)). Распознавание образов Основные подзадачи Основными подзадачами задачи распознавания являются: 1) создание исходного списка признаков; 2) выбор классов объектов; 3) подготовка таблицы (таблиц) обучения; 4) выбор семейства решающих правил; 5) поиск оптимального (относительно некоторого критерия или критериев) решающего правила в этом семействе; 6) подготовка описаний проб; 7) распознавание проб. На этапах 1 - 3 производится выбор и экспликация признаков (см. пособие Красавчикова, 2008) и составление базы данных. При создании исходного перечня признаков могут быть реализованы два подхода: А) всестороннее описание объектов, характерное для ситуаций, когда исследователь не знает, из каких признаков должен быть составлен окончательный список (информативная система признаков), по которому будет производиться распознавание проб. Поэтому он отбирает такие признаки, которые, в принципе, могут содержать полезную информацию (хотя, на первый взгляд, их связь с решаемой задачей может быть и не очевидна), и полагается в выборе информативной системы признаков на алгоритм и реализующую его программу. Б) описание объектов, основанное на некоторой геологической модели, для которой список признаков заранее известен. При выборе классов объектов исходят не только из постановки задачи (например, разбраковать локальные поднятия на перспективные и бесперспективные по результатам интерпретации данных сейсморазведки), но и основываются на геологическом смысле и опыте решения аналогичных задач. Возможно, придётся проводить декомпозицию задачи и осуществлять поэтапное решение в рамках последовательно-параллельной блок-схемы несколько задач распознавания. При подготовке таблицы (таблиц) обучения следует, по-возможности, избегать появления характеристических признаков, замеренных в шкале наименований (номинальных) с числом принимаемых ими значений, превосходящим два, поскольку они резко ограничивают выбор алгоритма распознавания. Они могут содержать весьма существенную информацию, но лучше, чтобы они не входили в список характеристических признаков. Обычно, по значениям таких признаков формируются классы. Выбор семейства решающих правил не является формальной процедурой. Однако, при этом выборе есть и формальные требования. Например, если среди признаков есть номинальные или ранговые, то можно использовать только те алгоритмы, которые способны работать с информацией, представленной в качественных шкалах. Одним из главных критериев выбора решающего правила является его «простота». Практика показала, что предпочтение следует отдавать более простым решающим правилам. Если среди «простых» решающих правил (причём, доступных исследователю в программной реализации) не удаётся найти способного справиться с поставленной задачей (или, в случае (а), радикально сократить размерность описания), то переходят к более сложным и т.д. Формализовать понятие простоты не так-то просто! В математической логике и теории алгоритмов есть целое направление, связанное с формализацией и изучением простоты математических конструкций, но знакомство с этой тематикой не входит в задачи курса. Поэтому будем относиться к этой проблематике как интуитивно ясной. По всей видимости, примером наиболее простых решающих правил могут служить линейные (см. ниже). Если есть два линейных решающих правила, то более простым, очевидно, является то, которое использует меньшее число признаков. В случае (а) при выборе семейства решающих правил следует обращать особое внимание на способность радикального сокращения размерности описания. После выбора семейства проводится поиск решающей функции и соответствующего правила, которые в этом семействе обладают «наилучшим качеством» по отношению к материалу обучения и экзамена. Для оценки качества решающего правила используются функционалы наподобие нижеприведённого: Δ(F,λ,ε)=p1M1 + p2M2 +p3M3 + p4M4, где для материала обучения и экзамена M1 – число ошибочно распознанных объектов первого класса; M2 – число ошибочно распознанных объектов второго класса; M3 – число отказов для объектов первого класса; M4 – число отказов для объектов второго класса. Коэффициенты pj, j=1,…,4, – «штрафы» за ошибку соответствующего типа. Чем меньше значение Δ(F,λ,ε) (при фиксированных списках объектов обучения и экзамена), тем выше качество решающего правила. После того, как для всех объектов обучения и экзамена вычислены значения решающей функции, управляющие параметры алгоритма λ, ε могут быть выбраны оптимальным образом, т.е. так, чтобы функционал качества решающего правила достигал минимума: Δ(F,λ*,ε*)=min Δ(F,λ,ε), где минимум берётся по всемλ, ε и ε>0. В случае (а) ещё одним (и не менее важным) критерием качества является резко сокращение числа признаков, используемых в распознавании, по сравнению с исходным списком. Это обусловлено тем, что - малое число признаков уменьшает влияние «информационных шумов», что делает распознавание более надёжным; - сокращается время на подготовку описаний проб. Так, при распознавании в узлах сеток уменьшается число карт, которые приходится строить; - появляется возможность содержательно проинтерпретировать решающее правило и т.д. Описание проб производится по признакам, используемым в оптимальном решающем правиле. В случае (а) это особенно важно, т.к., в частности, существенно сокращается время на подготовку описаний.
|
||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 242; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.91.130 (0.007 с.) |

 , где i =1,…m соответственно. Одним из наиболее применяемых в анализе данных методов прикладной статистики является метод множественной линейной регрессии. Задача множественной линейной регрессии может быть сформулирована следующим образом (Дрейпер, Смит, 1973). Для линейной модели
, где i =1,…m соответственно. Одним из наиболее применяемых в анализе данных методов прикладной статистики является метод множественной линейной регрессии. Задача множественной линейной регрессии может быть сформулирована следующим образом (Дрейпер, Смит, 1973). Для линейной модели .
.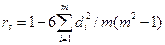 ,
,


