
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сведение задачи уточнения границы геологического телаСодержание книги Поиск на нашем сайте
к решению задачи распознавания образов Для моделирования геологических тел различных масштабов в осадочном бассейне (ОБ) необходимо знать их границы (по латерали), не только внешние, но и внутри зоны сплошного распространения. Как показывает опыт решения многочисленных практических задач, для этого могут быть с успехом применены методы распознавания образов. Сформулируем задачу нахождения проекции границы геологического тела на земную поверхность по косвенным признакам как задачу распознавания. Пусть имеем двухмерную равномерную координатную сетку K, заданную в прямоугольнике Q, горизонтали и вертикали которой параллельны соответствующим осям координат, K= {(x1,y1),(x2,y2), …,(xk,yk)}. Определение. Равномерной сеткой (гридом) G называется частично определённая вещественная функция, заданная на K. Объекты обучения S1,…,Sm и пробы Pk, k=1,2, … – вертикальные разрезы, исходящие из точек земной поверхности. Pkисходят из узлов двухмерной равномерной координатной сетки K. Для всех Si и Pk известны значения признаков X1,…,Xn. Пусть наличие или отсутствие тела G установлено в разрезах S1,…, Sm. В первых m(1) из них тело присутствует, востальных – нет.Требуется: 1) найти решающую функциюF(u1,…,un)ичислоw, такие, что F(X1(Si),…,Xn(Si))>wприi=1,…,m(1) и F(X1(Si),…,Xn(Si))≤w при i=m(1)+1,…,m; 2) используя найденное решающее правило, распознать Pk на наличие в них тела G; 3) по результатам распознавания Pkпровести искомую проекцию.
Примеры алгоритмов распознавания К настоящему времени опубликованы сотни методов распознавания. Они объединяются в семейства. Зачастую, эти семейства описываются в виде решающих функций (либо правил) с неопределёнными параметрами. Устоявшейся общепризнанной классификации семейств алгоритмов распознавания не существует. Поэтому ограничимся кратким описанием нескольких семейств алгоритмов, показавших свою эффективность при решении прикладных геологических задач, особенно в геологии нефти и газа. Для подробного ознакомления с применением методов распознавания в геологии нефти и газа отсылаем читателя к публикациям 60-80 годов прошлого века, когда их использование при решения задач прогнозно-поискового профиля было массовым. Методы распознавания применялись, в частности, при решении задач прогноза гигантских нефтяных месторождений, продуктивности локальных поднятий, фазового состояния УВ в залежах и др. (Распознавание образов…, 1971; Раздельное прогнозирование…, 1978, Прогноз месторождений …, 1981 и др.).
4.3.1. Байесовские решающие правила Эти решающие правила подробно охарактеризованы в учебном пособии Дёмина (2005), куда мы и отсылаем читателя. Для более глубокого ознакомления с приложениями байесовской теории принятия решений в геологии нефти и газа рекомендуем обратиться к монографии (Прогноз месторождений…, 1981).
4.3.2. Комбинаторно-логические методы в распознавании Применение этих методов рассмотрим на примере одной конкретной схемы распознавания, основанной на аппарате дискретной математики и математической логики. Пусть сначала для простоты изложения все признаки X1,…,Xn – бинарные. Согласно Журавлёву (1978) назовём произвольную совокупность W наборов признаков вида w=(Xj(1),…,Xj(k)), где k=1,…,n, системой опорных множеств, W={w1, w2,…, wN}, а её элементы wr – опорными множествами. Пусть wÎW, w=(Xj(1),…,Xj(L)), Sk – строка таблицы Определение 1. Набор признаков wÎW голосует за отнесение строки S к первому классу, если в таблице T1 найдётся строка Sk, такая, что по набору w строки S и Sk не различаются; w голосует за отнесение строки S ко второму классу, если в таблице T2 найдётся строка Qp, такая, что по набору w строки S и Qp не различаются. Пусть Г1(S), Г2(S) – числа голосов по всем wÎW за отнесение строки S к первому и второму классам соответственно. Тогда решающее правило имеет вид: при Г1(S) >
при Г2(S) > в остальных случаях S не распознаётся.
Смысл этого решающего правила заключается в том, что для отнесения пробы S к классу Kj, где j=1,2, она должна получить – больше голосов за класс Kj, чем любой объект противоположного класса; – не больше голосов за противоположный класс, чем самый близкий к этому классу объект обучения класса Kj. Близость здесь оценивается числом голосов за класс.
Эта схема представляет собой один из простейших вариантов голосования по системе опорных множеств. Алгоритм представляет собой реализацию так называемого «принципа частичной прецедентности» (Журавлёв, 1978), при котором заключение о принадлежности объекта к классу выносится на основе анализа совпадений фрагментов его описания с соответствующими фрагментами описаний объектов этого класса. Совпадение фрагментов описаний объекта обучения и пробы является частичным прецедентом. Пример системы опорных множеств: тестовая конструкция. Её основой являются понятия теста и тупикового теста, предложенные С.В. Яблонским в качестве математического аппарата диагностики технических устройств (Журавлёв, 1978). Определение 2. Набор столбцовw называется тестом для пары таблиц T1, T2 если по нему нет совпадений между строками Si и Qp, где Определение 3. Тест называется тупиковым, если из него нельзя удалить ни одного столбца без того, чтобы он перестал быть тестом. Дмитриев, Журавлёв, Кренделев (1966) воспользовались аппаратом тупиковых тестов для создания алгоритмов классификации предметов и явлений. В геологии нефти и газа комбинаторно-логические методы впервые были применены при решении задач прогноза гигантских нефтяных месторождений (Распознавание образов …, 1971), где была использована тестовая конструкция. Под руководством А.А. Трофимука тестовый подход применён также и к решению других важнейших прогнозных задач геологии нефти и газа (Раздельное прогнозирование…, 1978 и др.). Ряд сделанных А.А. Трофимуком прогнозов, не нашедших поддержки в момент опубликования, в дальнейшем блестяще подтвердились. Константиновым, Королёвой, Кудрявцевым (1976) на представительном фактическом материале по прогнозу рудоносности была подтверждена эффективность алгоритмов тестового подхода по сравнению с другими алгоритмами распознавания, применявшимися для решения задач рудопрогноза. В геологии нефти и газа другие системы опорных множеств не применялись. Если в таблицах встречаются признаки, замеренные в количественных шкалах, то для них используются пороговые меры различимости значений (см. Красавчиков, 2009). 4.3.1. Линейные методы Линейные методы стали применяться для решения задач распознавания образов одними из первых (см.. Ту, Гонсалес, 1978) в середине прошлого века. Пусть F(u1,…,un)=a1u1 + a2u2 + … +anun – линейная функция n переменных u1,…,un. Методы отыскания линейных решающих функций и правил принято называть линейными. Общий вид линейных решающих правил может быть задан следующим образом: при a1X1(S) + a2X2(S) + … +anXn(S)≥λ+ε объект S относится к К1; при a1X1(S) + a2X2(S) + … +anXn(S)≤λ-ε объект S относится к К2; при λ-ε <a1X1(S) + a2X2(S) + … +anXn(S)<λ+ε объект S не распознаётся. Пусть
где j=1,…,n, i=1,…,m(1), k=m(1)+1,…,m c неизвестными y1,…,yn (искомыми значениями коэффициентов aj) и λ. Для проверки существования решения систем линейных неравенств используются вычислительные методы линейной алгебры; эта проверка является «не слишком сложной», а программное обеспечение содержится в общераспространённых пакетах. Если решение существует, то оно либо единственно, либо их бесконечно много.
Существуют многочисленные методы нахождения линейных решающих правил, реализующие различные дополнительные требования (типа максимизации ε, сокращения размерности описания и пр.). Геометрическая интерпретация линейного решающего правила заключается в следующем. Пусть все признаки замерены в количественных шкалах и En – n-мерное евклидово пространство. Гиперплоскость a1 x 1+a2 x 2+…+an x n= λ делит En на две части таким образом, что в каждой из них находятся точки только одного из классов. Такие гиперплоскости называются разделяющими. Ситуация заметно усложняется, если разделяющей гиперплоскости не существует и нужно отыскать гиперплоскость, минимизирующую функционал качества распознавания. С вычислительной точки зрения эта задача является намного более сложной. Линейные методы распознавания использовались в течение ряда лет для прогноза продуктивности локальных поднятий и уточнения границ природных резервуаров УВ в нижне -среднеюрских отложениях Западной Сибири (Каштанов, Соколов, 1976, Красавчиков, 2007).
Упорядочение На практике вместо отыскания решающей функции, удовлетворяющей цепочке неравенств (1), зачастую достаточно получить «хорошую» корреляцию упорядочения по убыванию значений функции F с упорядочением на материале обучения. Это имеет принципиальное значение, поскольку решающей функции, для которой выполняются неравенства (1), в классах «простых» функций (типа линейных и т.п.) может и не существовать. Для приближённого решения этой задачи можно применять математический аппарат множественной линейной регрессии, реализованный в программном продукте Statistica for Windows. Пусть приближённое решение F ищется в классе линейных функций, F(u1,u2,…,un)= a 1u1+ a2 u2+…+ an un+ b, где a 1,…, a n, b – коэффициенты при переменных и свободный член соответственно, Ψ – некоторая монотонная функция, определённая на множестве значений целевого признака (например, логарифм, см. пояснение в разделе 10). Тогда, решая задачу множественной линейной регрессии вида: найти a 1,…, a n, b, при которых функционал
достигает минимума, мы получаем приближённое решение задачи упорядочения через аппроксимацию некоторой монотонной функции от целевого признака. Поскольку функция Ψ монотонна, можно, используя коэффициент Спирмена, оценить достоверность связи между решением регрессионной задачи и значениями целевого признака X n+1. Значение rs является естественным показателем качества приближённого решения задачи упорядочения.
Можно показать, что для отыскания точного решения F в классе линейных решающих функций достаточно решить систему m-1 нестрогих линейных неравенств c n неизвестными p 1,…, p n:
где n – число признаков, e>0 – малая положительная константа. При этом, как легко видеть, разности Xj(Si) - Xj(Si+1)=Hij являются известными величинами. Обратно, из существования решения системы линейных неравенств (3) вытекает существование решения системы неравенств (2). Однако, как уже отмечалось, в классе линейных решающих функций решения может и не существовать. Программное обеспечение для решения систем нестрогих линейных неравенств отсутствует в пакете Statistica. Однако оно, в принципе, является достаточно распространённым и содержится в программных продуктах, предназначенных для решения задач вычислительной алгебры.
Кластер-анализ Существует большое количество методов и алгоритмов кластер анализа. Среди них выделяются две крупные группы, к которым относится большинство опубликованных алгоритмов. Это иерархические алгоритмы, порождающие древовидные классификации объектов, и алгоритмы, порождающие разбиения (группировки).
Иерархические алгоритмы Среди иерархических алгоритмов можно выделить два основных класса – агломеративные и дивизимные. Это – пошаговые алгоритмы. Агломеративные алгоритмы начинают с того, что каждый объект является отдельным кластером, а заканчивают тем, что все кластеры объединяются в один объект. На каждом шаге производится объединение двух наиболее «близких» в некотором смысле кластеров. Близость между кластерами задаётся «расстоянием» либо мерой близости. Под «расстоянием» в данном случае понимается неотрицательная симметричная функция. Примеры таких функций будут рассмотрены ниже. В дивизимных же методах, наоборот, на первом шаге все объекты образуют один кластер, на последнем – каждый объект представляет отдельный кластер.
6.1.1. Агломеративные алгоритмы Рассмотрим агломеративные методы, представленные в пакете Statistica for Windows. Для этого сначала определим функции, с помощью которых оцениваются расстояния между конечными подмножествами метрического пространства M. Пусть множество описаний объектов S= {S1,…,Sm} признаками X1(S),…,Xn(S) содержится в евклидовом пространстве En, так что для любой пары объектов Si, Sj из S определена метрика (расстояние) ρij= ρ(Si,Sj) и можно составить симметричную матрицу расстояний R=(ρij)m´m. Приведём примеры функций двух переменных, значения которых играют в кластер-анализе роль расстояний между непересекающимися подмножествами, хотя, формально, эти функции не являются метриками. Пусть Al, Aq Ì S неимеют общих элементов, AlÇAq = Æ. Тогда: а) ρlq равно расстоянию между двумя ближайшими объектами множеств Al, Aq;. б) ρlq равно расстоянию между самыми далекими объектами множеств Al, Aq; в) ρlq равно расстоянию между центрами тяжести множеств Al, Aq (точек со средними значениями всех показателей); г) ρlq равно среднему арифметическому расстояний между объектами множеств Al, Aq;
д) ρlq равно расстоянию между точками с медианными значениями признаков для мно- жеств Al, Aq; е) ρlq равно сумме расстояний между элементами множеств Al, Aq. ж) ρlq равно так называемому «статистическому расстоянию» (Дюран, Оделл, 1977) между множествами Al, Aq:
Здесь В иерархических агломеративных алгоритмах, основанных на вычислении «расстояний» между подмножествами Al, Aq вида (а-ж) и им подобных, на первом шаге каждый объект считается отдельным кластером. На следующем шаге объединяются два ближайших объекта, которые образуют новый класс, определяются «расстояния» от этого класса до всех остальных объектов. Матрица расстояний, соответственно, изменяется с учётом результатов кластеризации, включая уменьшение её размерности. На р-м шаге для кластеров и матрицы расстояний предыдущего шага Rp-1 повторяется та же процедура, пока все объекты не объединятся в один кластер. В отличие от R1=R, при p>1 элементами Rp являются не расстояния между объектами, а «расстояния» между кластерами. Если сразу несколько объектов (либо кластеров) имеют минимальное «расстояние», то возможны две стратегии: выбрать одну случайную пару или объединить сразу все пары. Первый способ является классическим; иногда в литературе его называют восходящей иерархической классификацией. Второй способ используется гораздо реже. Метод, основанный на вычислении «статистического расстояния» (см. п. (ж) выше) называется методом Уорда (Мандель, 1988) по имени предложившего его специалиста. Названия остальных методов определяются используемым в них расстоянием. Результаты работы всех иерархических агломеративных процедур обычно оформляются в виде так называемой дендрограммы (см. рис. 1), в которой по горизонтали показаны номера объектов, а по вертикали – значения межкластерных расстояний ρlq, при которых произошло объединение двух кластеров.
6.1.2. Дивизимные алгоритмы Этот класс алгоритмов кластер-анализа опишем на примере «Быстрого дивизимного комбинационного алгоритма», предложенного Chaudhuri (Мандель, 1988). Проведённые в ИНГГ эксперименты показали его высокую эффективность при решении задачи кластеризации разрезов по толщинам составляющих их горизонтов на основе информации, содержащейся в сетках толщин. Обработка информации по средней юре юго-востока ЗСП показала, что он быстро и «разумно» кластеризует огромные массивы данных, представленных сеточными моделями. Другими алгоритмами кластеризовать эти массивы, состоящие, порой, из миллиона с лишним объектов, охарактеризованных более чем 10 признаками, часто невозможно либо крайне затруднительно. Алгоритм Chaudhuri (Чаудури) в программном продукте “Statistica for Windows” не представлен. Этот алгоритм для краткости будем называть также алгоритмом гиперкубов. Приведём его краткое описание. Гиперкуб, в котором содержатся все точки (определяемый размахами вариации признаков), разбивается на первом шаге по каждой оси перпендикулярной ей плоскостью на 2 n «кубика», где n –число признаков. На j -м шаге каждый из этих кубиков также разбивается, т. е. получается 2 n j гиперкуба. Если в полученном кубе есть хоть один объект, он считается заполненным, если нет – пустым. Кластером здесь называется максимально большая связная область, в которой любые два объекта соединены непустыми клетками (т.е. компонента связности графа, вершинами которого являются объекты, и две вершины в котором соединены ребром если и только если они либо находятся в одной клетке либо вмещающие их клетки имеют общую границу, пусть даже состоящую из одной точки). По мере увеличения j число кластеров растет, т.е. алгоритм носит дивизимный характер. Он принадлежит к числу наиболее быстрых иерархических алгоритмов, не требует предварительной нормировки показателей, хранения и пересчёта матрицы расстояний, может работать в исходном пространстве. Эти и некоторые другие особенности относят его к числу наиболее предпочтительных алгоритмов для построения иерархических классификаций в случае больших баз данных.
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.152.33 (0.014 с.) |

 , Qp – строка таблицы
, Qp – строка таблицы  . Строки Sk и Qp различаются по набору признаков w, если найдётся входящий в w признак Xj(r) такой, что Xj(r)(Sk)¹Xj(r)(Qp). В противном случае будем говорить, что они не различаются.
. Строки Sk и Qp различаются по набору признаков w, если найдётся входящий в w признак Xj(r) такой, что Xj(r)(Sk)¹Xj(r)(Qp). В противном случае будем говорить, что они не различаются. Qp) и Г2(S) ≤
Qp) и Г2(S) ≤ 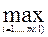 Г2(Si) объект S относится к классу K1;
Г2(Si) объект S относится к классу K1; Si) и Г1(S) ≤
Si) и Г1(S) ≤  Г1(Qp) объект S относится к классу K2;
Г1(Qp) объект S относится к классу K2; ,
, 

 , i=1,…,m-1, (3)
, i=1,…,m-1, (3) .
. – векторы средних значений признаков для подмножеств Al, Aq, T – знак транспонирования. Таким образом, «статистическое расстояние» между подмножествами Al, Aq представляет собой квадрат расстояния между векторами средних значений признаков (центрами тяжести)
– векторы средних значений признаков для подмножеств Al, Aq, T – знак транспонирования. Таким образом, «статистическое расстояние» между подмножествами Al, Aq представляет собой квадрат расстояния между векторами средних значений признаков (центрами тяжести) 


