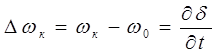Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды пп в ээс и анализ эл. Мех-х пп.Стр 1 из 6Следующая ⇒
Виды ПП в ЭЭС и анализ эл.мех-х ПП.
При переходах системы от одного исходного установившегося режима к другому происходит изменение количества энергии. Это явление при анализе принимается состоящим из ряда процессов, каждый из которых отражает изменение определенной группы параметров режима. при решении задач важно учитывать только наиболее существенные в данной задаче факторы. При этом различают ПП по ряду признаков: по причинам возникновения или по видам возмущающих воздействий и величинам возмущений. Под возмущением при этом понимают отклонения параметров режима, происходящие в начале ПП в связи с появлением новых, т.е. не проявляющихся ранее, факторов, изменяющих режим. Эти факторы называются возмущающими воздействиями; по допущениям, сделанным при составлении и решении дифференциальных уравнений, т.е. по математическому описанию; по скорости протекания этих процессов в системе (от 10-7 до 105 с); по структуре исследуемой системы. При рассмотрении причин возникновения ПП можно различать или реальные физические причины ПП или, независимо от этих физических причин, большие возмущения, изменяющие исходную систему на какое-то время и нарушающие ее исходный режим, или малые возмущения, которые появляются во время нормальной работы системы. Градация ПП по допущениям сделанным при математическом их описании, особенно разнообразна, поэтому ограничиваются только наиболее существенными признаками. Например, анализ реальной нелинейной системы может проводиться при учете имеющихся нелинейностей или замене нелинейных зависимостей параметров режима линейными. По линеаризованным уравнениям проводятся как исследования статической устойчивости, так и исследования, связанные с оценкой показателей качества ПП. По нелинейным уравнениям проводятся исследования динамической и результирующей устойчивости и ПП после больших возмущений. Ряд допущений, принимаемых при исследованиях эл.мех-х ПП, основывающихся на методах электротехники, механики, теории колебаний, имеет свои существенные особенности. Например, при рассмотрении электричесих систем переменного тока можно оперировать мгновенными значениями тока и напряжения и составлять применительно к ним уравнения.
Важные допущения, принимаемые при анализе эл.мех-х ПП, касаются учета изменений скорости роторов СМ, реакции якоря в них и электромагнитных процессов в АМ. При процессах, связанных с синусоидальными изменениями параметров режима основной рабочей частоты (50 Гц), обычно рассматриваются не мгновенные значения, а их огибающие. Анализ, проводимый без этого упрощения, называется или анализом по полным уравнениям с учетом влияния изменения мгновенных значений, или анализом в мгновенных значениях, или анализом по уравнениям Парка-Горева. При расчете по огибающим изменения электрической мощности принимаются происходящими мгновенно. Все упрощения анализа ПП заключаются в выделении главного, практически существенного для решения поставленных задач. Одним из упрощающих приемов, широко применяемых при анализе ПП, является замена реальных динамических характеристик элементов электрических систем их статическими характеристиками, а также рассмотрение динамической электрической системы как системы позиционной (позиционная система – это система, энергия которой есть функция от состояния).
Виды ПП в ЭЭС и анализ эл.мех-х ПП. Под статическими характеристиками понимаются графически или аналитически представленные связи каких-либо параметров режима с другими его параметрами и параметрами системы. Эти связи выявляются в условиях установившегося или переходного режима системы, но при допущениях, позволяющих считать эти связи не зависящими от времени. Под динамическими характеристиками понимаются взаимосвязи параметров, полученные в условиях, когда указанные параметры или часть их зависят от времени.
Проблема устойчивости установившегося режима.
В установившемся режиме энергия WГ, поступающая в систему извне (для генераторов электрической системы энергией, приходящей извне – поступающей в систему, будет механическая энергия первичных двигателей), расходуется в нагрузке и идет на покрытие потерь. При каком-либо возмущении, проявляющемся в изменении на ΔП определяющего режим параметра П, т.е. параметра, от которого зависит режим (определяющий параметр только один), этот баланс нарушается.
Если свойства системы таковы, что расход энергии W=WН+ΔW после возмущения будет происходить более интенсивно, чем увеличение энергии, которую может дать после возмущения внешний источник [WГ =f(П)], то новый (возмущенный) режим не может быть обеспечен энергией и в системе должен восстанавливаться прежний установившийся режим (или режим, близкий к нему). Такая система будет оценена как устойчивая. Из определения устойчивости следует, что математически записанным условием ее сохранения, или критерием устойчивости, будет условие: ΔW/ΔП>ΔWГ /ΔП; или в дифф-ой форме: d(WГ-W)/dП<0; или dΔWΣ Г/dП<0; где (WГ-W)=ΔWΣ Г и называется избыточной энергией. Режим устойчив, если производная от избыточной энергии по определяющему параметру П отрицательна. Избыточная энергия должна определяться с учетом всех влияющих процессов, и поэтому практически воспользоваться критерием при анализе устойчивости энергосистемы удается только в частных случаях с определенными упрощающими ограничениями. При этом, выясняя факт наличия или отсутствия устойчивости, критерий не дает непосредственных указаний о характере протекания процесса. Суждение об устойчивости обычно получают, оперируя не с полной энергией системы, а с некоторыми зависящими от нее величинами, выявляемыми (из практических соображений) для каждой конкретной задачи. Отсюда и появляются практические критерии устойчивости. Так, например, для генератора постоянного тока последовательного возбуждения, вращающегося с постоянной скоростью, условия устойчивости будут: d(E-U)/dI<0; или dU/dI>dE/dI; Критерий устойчивости простейшей электрической системы, режим которой зависит только от изменений угла, имеет вид: dPΣ /dδ<0; Или при PT=const; dP/dδ>0; где δ=(E^U); PΣ =PT –PЭЛ; Практический критерий устойчивости АД: dPΣ /dS<0, где PΣ =PМЕХ –P; При PМЕХ =P0 =const; dP/dS>0; То есть, устойчивыми будут режимы, при возмущении которых факторы, стремящиеся нарушить их, изменяются менее интенсивно, чем факторы, противодействующие этому нарушению.
Статические и динамические хар-ки элементов нагрузок. У рабочих машин разнообразные механические характеристики, могут быть сведены к трем основным видам зависимостей MМЕХ=f(ω): а) постоянный, или мало зависящий от скорости, момент: MМЕХ=const; PМЕХ≡ω; б) момент, примерно пропорциональный скорости: MМЕХ≡ω; PМЕХ≡ω2; в) момент, примерно пропорциональный квадрату скорости: MМЕХ≡ω2; PМЕХ≡ω3; где ω=ω0+Δω. В общем случае MМЕХ=M0ωn; т.е. при ω0=1, МЭЛ=М0(1+S)n+1=f(S). Т.к. реактивная мощность, потребляемая двигателем, имеет две составляющие: намагничивающую мощность Qμ и мощность рассеяния QS: Q=Qμ+QS; где QS=I2XS; Qμ=U2/Xμ =IμU; Iμ – ток ХХ. Характеристики синхронной нагрузки (СД): При изменении напряжения, подведенного к двигателю, его мощность и вращающий момент изменяются (если не учитывать потери в статоре) прямо пропорционально величине напряжения: P=(UEq/Xd)sinδ; M=P/ω0; Изменение частоты подведенного напряжения изменяет вращающий момент: M=(UEqoωn-2/Xd0)sinδ; где Xdo – величина сопротивления при ω=ω0; n – показатель, характеризующий систему возбуждения двигателя.
Характеристики комплексной нагрузки: Комплексная нагрузка состоит из осветительной и бытовой нагрузок, нагрузки двигателей, инверторов и выпрямителей, а также потерь в трансформаторах и кабелях. Ее динамические характеристики могут быть приближенно получены из серии статических характеристик. При малых изменениях напряжения и частоты статическую характеристику можно аппроксимировать линейной функцией: ΔP=(∂P/∂U)ΔU+(∂P/∂f)Δf; ΔQ=(∂Q/∂U)ΔU+(∂Q/∂f)Δf.
Полный сброс мощности. Рассмотрим движение ротора генератора под действием только механического момента турбины при Pm=0, т.е. без отдачи генератором мощности в сеть. Этот случай имеет большое практическое значение, отвечая трехфазному КЗ у шин генератора или отключению генератора от линии (X12=∞). При этом прекращается связь генератора с нагрузкой и вся мощность турбины (PМЕХ=P0) идет на ускорение ротора генератора. Это, следовательно, наиболее опасный случай в смысле разгона генератора и нарушения устойчивости. Дифференциальное уравнение:
при этом принимает вид: Tjd2δ/dt2=P0; Это уравнение интегрируется весьма просто. В самом деле движение происходит при постоянном ускорении α, причем α=dω/dt=P0/Tj. Интеграл этого уравнения: ω=αt. И соответственно δ–δ0=[P0/(2Tj)]t2; Рост скорости происходит линейно, а угла – по квадратичной параболе. Время t, отвечающее какому-либо значению угла δ, найдем из последнего уравнения:
Если бы в начальный момент (t=0) ротор имел некоторую скорость Δω0=0, то решение имело бы вид:
Влияние демпфирования и уменьшения момента турбины при полном сбросе мощности: Демпферные моменты, препятствующие движению, и уменьшение вращающего момента турбины с ростом скорости (уменьшение «естественное», вызванное трением, потерями на гистерезис, действием регуляторов скорости) изменяют характер движения, определенного уравнением: δ–δ0=[P0/(2Tj)]t2. Основное уравнение:
при учете демпфирования имеет вид:
PМЕХ=(1–аω)P0, тогда: Tj(dω/dt)+Kdω=P0; где Kd=Pd+P0a;
Решение последнего уравнения:
Следовательно, скорость не возрастает непрерывно, а экспоненциально стремится к некоторому установившемуся значению P0/Kd=ω∞. Из последнего уравнения легко найти изменение угла:
Таким образом, демпфирование, пропорциональное скорости, и уменьшение мощности турбины при увеличении скорости задерживают рост угла при сбросе мощности.
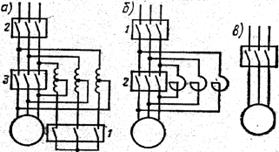
Пуск синхронных двигателей. В основном используются три схемы пуска: автотрансформаторный пуск (рис.а), реакторный пуск (рис.б) и прямой пуск (рис.в).
Условия пуска обычно разделяют легкие, нормальные и тяжелые. При легких условиях требуемый момент в начале вращения двигателя составляет 10÷40% от номинального. К нормальным условиям пуска относятся такие, при которых механизм требует пускового момента, равного 50÷75% от номинального. К тяжелым условиям относятся такие, при которых требуемый начальный момент составляет 100% номинального и выше. Пуск СД: СД при пуске подключаются сначала к сети невозбужденными. Их обмотки возбуждения при этом короткозамкнуты или замкнуты на сопротивление ΔR=(5÷10)RВ, где RВ – сопротивление обмотки возбуждения. Разгоняясь как асинхронные, они достигают скорости, близкой к синхронной (подсинхронная скорость). После этого двигателям подается возбуждение и они, приобретая свойства СД, входят в синхронизм. Т.о., процесс пуска СД можно разбить условно на два этапа (см. рис.): 1) разгон до подсинхронной скорости (s≈0,1) происходит в основном под действием среднего асинхронного момента; 2) вхождение в синхронизм под влиянием моментов, обусловленных возбуждением и зависящих от угла между осью ротора и вектором вращающегося поля статора. На первом этапе пуска существенны начальный толчок тока статора и длительность разгона до подсинхронной скорости. Начальный толчок периодической слагающей тока статора: I≈U/Х11dΣ; где U – напряжение сети в той точке, где оно может быть принято не зависящим от режима двигателя; Х11dΣ=Х11d+ХСТ, причем ХСТ – внешнее сопротивление цепи статора между точкой с напряжением U и выводами статора данного двигателя. Длительность разгона до подсинхронной скорости можно определять так же, как и для АД. Однако при проектировании ее обычно находят графо-аналитическими методами. Более точно изменение токов статора и ротора в процессе разгона двигателя может быть получено с помощью уравнений Парка-Горева. На втором этапе пуска на несинхронно вращающийся ротор СД кроме асинхронного момента действует синхронный момент, зависящий от угла δ и обусловленный возбуждением, а также момент сопротивления механизма. Практически вхождение в синхронизм может произойти только после подачи возбуждения, за счет которого у двигателя будет создан дополнительный момент, меняющийся по знаку (знакопеременный). Скорость вращения двигателя под воздействием знакопеременного момента будет колебаться около средней величины с двойной частотой скольжения. Поскольку на ротор действуют и другие знакопеременные моменты, а именно момент явнополюсности: MЯВН=(U2/2)[(Хd–Х1d)/(ХdХ1d)]; и переменная составляющая асинхронного момента, то иногда втягивание в синхронизм может произойти и без подачи возбуждения. Для этого, однако, необходимо, чтобы
Пуск синхронных двигателей.
втягивающий момент был больше механического: MЯВН>MМЕХ, что можно получить сравнительно редко. Характер процесса вхождения в синхронизм зависит от взаиморасположения ротора и магнитного потока статора в момент подачи возбуждения. Но положение ротора в момент подачи возбуждения обычно оказывает сравнительно малое влияние, поэтому можно не предусматривать специальных устройств для подачи возбуждения в наивыгоднейший момент.
Самозапуск двигателей. Самозапуск – это процесс восстановления нормального режима работы двигателей после кратковременного отключения источника питания. Задача самозапуска заключается в том, чтобы не допустить массового отключения электродвигателей. Самозапуск отличается от пуска тем, что: а)одновременно пускается целая группа двигателей; б)в момент восстановления питания какая-то часть или все двигатели вращаются с некоторой скоростью; в)самозапуск происходит под нагрузкой. По условиям самозапуска механизмы делятся на две группы: 1)механизмы, имеющие постоянный момент сопротивления и при кратковременном прекращении питания быстро теряющие скорость (транспортеры, прокатные станы, подъемные краны и т.п.); 2)механизмы, имеющие вентиляторные характеристики момента (центробежные насосы, вентиляторы, дымососы, центрифуги и др.). Самозапуск этой группы проходит легче, чем механизмов первой группы, т.к. момент сопротивления механизмов снижается при уменьшении скорости. Для обеспечения успешного самозапуска определяют суммарную мощность электродвигателей, которые могут быть запущены после перерыва питания. Суммарная неотключаемая мощность электродвигателей определяется при условии, что остаточное напряжение в режиме самозапуска обеспечивает вращающий момент, превышающий момент механизма. Расчет самозапуска предполагает решение нескольких задач: 1. Рассчитывается момент вращения двигателей при пониженном напряжении и проверяется его превышение над моментами механизмов. 2. Устанавливается температура дополнительного нагрева двигателей из-за увеличения времени разгона. Скольжение двигателей к моменту самозапуска может быть определено численным интегрированием уравнения движения ротора двигателя. Рассматривая самозапуск АД, предположим, что питание двигателей осуществляется по наиболее характерной схеме, показанной на рис.а. Напряжение на зажимах двигателей при самозапуске: UM=EСZЭКВ/(ZЭКВ+ХBH); (1) где ZЭКВ=ZMZH/(ZM+ZH); причем ZM - сопротивление эквивалентного двигателя, замедляющего все n подключенных двигателей; ХBH=ХС+ХT+ХL; - внешнее сопротивление. Сопротивление двигателя в момент самозапуска: ZM=U2HOM/SСЗ; (2) где SСЗ - суммарная мощность двигателей, самозапуск которых будет успешным; UHOM - номинальное напряжение двигателей.
Подставляя (2) в (1), найдем мощность SСЗ: SСЗ=(U2HOM/(ZHХBH))[EСZH/UM─(ZH+ХBH)]; (3)
Самозапуск двигателей. Мощность самозапуска связана с номинальной мощностью следующим образом (при КПД двигателей, равном 1): SСЗ=SHOMKS; (4) Причем
где К – кратность пускового тока. Подставляя (4) в (3), получаем выражение для мощности, которую можно назвать неотключаемой мощностью двигателей при самозапуске:
Минимальное допустимое напряжение на зажимах двигателей по условию осуществимости самозапуска для механизмов с постоянным моментом сопротивления определяется как:
Для механизмов с характеристиками вентиляторного типа:
где MM MIN – минимальный момент вращения двигателя, который часто принимают равным пусковому; MM MAX – максимальный момент вращения двигателя.
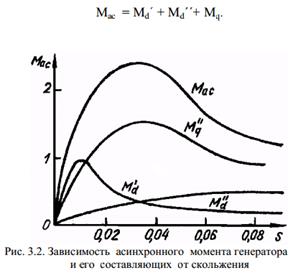
Асинхронные режимы в ЭЭС Очень важное значение имеют режимы работы электрических систем при больших отклонениях скорости вращения роторов генераторов или двигателей от синхронной. К таким режимам, например, относятся: работа синхронной машины на шины, где частота отлична от частоты этой машины, ресинхронизация после нарушения устойчивости, самосинхронизация генераторов, автоматическое повторное включение с самосинхронизацией или без контроля синхронизма, асинхронный пуск двигателей и компенсаторов, самозапуск двигателей. Все эти режимы, по различным причинам возникающие в системе, называются асинхронными. Для асинхронных режимов характерно периодическое изменение вектора э.д.с. хотя бы одной станции системы на угол, больший 360°. Эта станция называется работающей или идущей асинхронно. На рис. 14.1,а показано, как меняется положение вектора э.д.с. E одной из станций системы при больших качаниях, когда вектор перемещается из положения 1 в положение 2, и при асинхронном ходе этой станции, когда из положения 1 вектор перемещается в положение 3, «обогнав» вектор напряжения U. На рис. 14.1 ,б,в показано, что мощность синхронной машины, обусловленная ее возбуждением, меняется в зависимости от угла и времени примерно по синусоидальному закону.
При асинхронном ходе и скорости больше синхронной генератор, работая как асинхронный, выдает активную мощность, которая называется асинхронной. Если бы генератор был идеально симметричен, то асинхронная мощность при данном скольжении была бы постоянной. Наличие несимметрии (явнополюсность, одноосная обмотка возбуждения и т. д.) приводит к тому, что асинхронная мощность пульсирует около некоторого среднего значения — средней асинхронной мощности (рис. 14.2).
Асинхронные режимы в ЭЭС Средняя асинхронная мощность зависит от типа и конструкции генератора и от величины среднего скольжения (рис. 14.3). Во время асинхронного хода изменяется не только мощность P, но и токи статора I и ротора IВ, а также результирующее потокосцепление обмотки возбуждения — э.д.с. E’q. Э.д.с. Eq и E’q пульсируют около некоторого среднего значения. В первом приближении можно считать, что в начале установившегося асинхрон ного режима ток, активная и реактивная мощности определяются значением э.д.с. Eq исходного режима, если выпадение из синхронизма генератора, не имеющего регулятора возбуждения, происходило медленно. Если генератор имеет регулятор возбуждения, поддерживающий постоянство результирующего потокосцепле-ния с обмоткой возбуждения, или выпадение произошло в результате резкого возмущения (например, короткого замыкания), то можно грубо полагать, что параметры установившегося асинхронного режима определяются э.д.с. E’q0, отвечающей исходному режиму. В сложных электрических системах могут быть два случая, когда из синхронизма на станции одновременно выходят несколько генераторов или несколько станций. При анализе вся эта группа генераторов заменяется одним эквивалентным. Такая замена может быть сделана довольно приближенно при соблюдении ряда условий и, прежде всего при условии, что параметры всех объединяемых генераторов и их удаленность от узловой точки примерно одинаковы. Постоянная инерции эквивалентного генератора в этом случае находится, как обычно, суммированием приведенных к базисной мощности постоянных инерции отдельных генераторов. Момент эквивалентного генератора принимается равным сумме моментов объединяемых генераторов. Существенное влияние на асинхронный ход оказывает регулятор скорости. Для регулятора скорости эквивалентного генератора рекомендуется принять средневзвешенное значение соответствующих параметров серводвигателей и регуляторов, установленных на эквивалентируемых генераторах: эквивалентная постоянная серводвигателей
эквивалентный коэффициент неравномерности
Причины появления асинхронного режима генератора или части системы могут быть весьма различными. Его может вызвать исчезновение возбуждения, нарушение динамической устойчивости после резкого возмущения или нарушение статической устойчивости сильно перегруженной системы при малом возмущении.
Результирующая устойчивость Характеризует способность системы самопроизвольно восстанавливать синхронную работу после кратковременного нарушения устойчивости. Если выпавшая из синхронизма система после устранения причины нарушения устойчивости вновь втягивается в синхронизм, то считают, что система с подключенными к ней генераторами обладает результирующей устойчивостью. При расчете переходных процессов, вызванных нарушением устойчивости, пользуются понятиями асинхронного режима и асинхронного момента. Асинхронным называется режим работы системы при больших отклонениях частоты вращения роторов генераторов или двигателей от синхронной частоты. Выпадение генератора из синхронизма сопровождается резким повышением частоты вращения ротора. При асинхронном ходе и частоте, большей чем синхронная, генератор работает как асинхронный и генерирует активную мощность, которая называется асинхронной. Причинами появления асинхронного режима могут быть: исчезновение тока возбуждения, нарушение динамической устойчивости после резкого возмущения, нарушение статической устойчивости сильно перегруженной системы при слабом возмущении. Возникновение асинхронного режима приводит к различным нарушениям нормальной работы СЭС: могут появляться периодические понижения напряжения, при которых затормаживаются двигатели и отключаются пускатели в сети напряжением 0,4 кВ, а также понижается устойчивость параллельной работы генераторов в синхронно работающих частях ЭЭС; из-за снижения напряжения и увеличения тока может нарушаться селективная работа релейной защиты, возникают колебания активной мощности, при которых появляется знакопеременный момент на валу турбины, приводящий к дополнительным механическим усилиям, возможно возникновение резонансных колебаний, опасных для оборудования и синхронной работы частей ЭЭС. При наличии между отдельными частями ЭЭС большого активного сопротивления увеличивается дефицит активной мощности в приемной части системы. В асинхронном режиме генератор кроме момента, обусловленного его возбуждением, развивает еще и асинхронный момент под действием свободных токов, которые возникают в его обмотке возбуждения и демпферных контурах из-за движения ротора по отношению к полю, созданного внешними эдс. Наличие несимметрии генератора, явнополюсность, одноосность обмотки возбуждения и т.д. приводят к тому, что его асинхронная мощность пульсирует около некоторого среднего значения. Аналогично изменяются реактивная мощность и напряжение. Таким образом, асинхронный момент генератора может быть представлен в виде двух составляющих: среднего асинхронного момента и знакопеременного. Первый зависит от типа и конструкции генератора, а также от среднего скольжения, второй не оказывает существенного влияния на протекание асинхронного режима, и им в расчетах пренебрегают. Средний асинхронный момент генератора, подключенного непосредственно к шинам неизменного напряжения, имеет три составляющие, которые обусловлены действием обмотки возбуждения, а также демпферных продольной и поперечной обмоток (рис.3.2):
Результирующая устойчивость
Регулирование частоты в ЭЭС В ЭС состоящей из ряда станций различают следующие изменения частоты: - быстрые и средние, происходят во время пп, связаны с изменением скорости г-ров под влиянием небалансов невращающих моментов на валах г-ров. - медленные харавтерно для системы в целом из-за инерции всех машин системы и действия АРЧВ и АРЧ. Рассмотрим быстрое изменение: При балансе момента, мощности на валу каждого г-ра. Мк=Ммех.к. k=1,2,...n и вращение ротора каждого генератора со скоростью ωк=ωо. Токи и напряжения изменяются с частотой fо= ωо/2п во время работы может возникнуть небаланс м/у мощностью и потребителем нагрузки и мощностью отдаваемой генератором. ▲М=Ммех-М следовательно возникнет изменение скорости генератора
и соответственно мгновенной частоты
Т.о. на 1 этапе происходит снижение или увеличение средней частоты в системе. Возникают качания г-ров относительно друг друга и за счет синхронных сязей происходит изменения значений мгновенных изменений частоты отдельных станций. Медленные изменения – f достигает значения выходящую за пределы зоны нечувствительности АРЧВ, которые вступают в работу и перераспределяют доп. нагрузку. Затем влияние оказывает медленнее действующий АРЧ, изменяют уставки первичных регуляторов регулирующих частоту на станциях которая принемает на себя небаланс мощностей и при наличии достаточного резерва мощности частота в системе восстанавливается до нормального значения. Время действия АРЧ несколько десятков секунд и процесс регулирования f считают медленным. Это позволяет в реальных случаях рассматривать эти процессы раздельно. Т.о. процесс изменения частоты в системе небаланса мощностей можно описать следующим образом 1) Относительно быстрые электромагнитные и электромеханические пп при которых АРЧВ и АРЧ не действуют. 2) Электромеханические пп средней скорости при действии регуляторов АРЧВ. 3) Медленные пп происходящие при действии АРЧ. Рассматривая 2 и 3 стадию пп можно исходить из того что уст. отключение f в системе зависит от баланса мощности в виде
δк=1/Кк – статизм агрегата. чем больше тем меньше отключение частоты при данном изменении мощности. Мгновенное изменение частоты для каждого генератора начале различны а после пп становятся одинаковыми.
Суммарное изменение мощности в системе м/о записать в виде: К∑ - суммарная энергия регулирования Характер выравнивания частоты, изменение ее значений в отдельной точке системы после возмущения зависят главным образом от параметров элементов входящих в систему.
Виды ПП в ЭЭС и анализ эл.мех-х ПП.
При переходах системы от одного исходного установившегося режима к другому происходит изменение количества энергии. Это явление при анализе принимается состоящим из ряда процессов, каждый из которых отражает изменение определенной группы параметров режима. при решении задач важно учитывать только наиболее существенные в данной задаче факторы. При этом различают ПП по ряду признаков: по причинам возникновения или по видам возмущающих воздействий и величинам возмущений. Под возмущением при этом понимают отклонения параметров режима, происходящие в начале ПП в связи с появлением новых, т.е. не проявляющихся ранее, факторов, изменяющих режим. Эти факторы называются возмущающими воздействиями; по допущениям, сделанным при составлении и решении дифференциальных уравнений, т.е. по математическому описанию; по скорости протекания этих процессов в системе (от 10-7 до 105 с); по структуре исследуемой системы. При рассмотрении причин возникновения ПП можно различать или реальные физические причины ПП или, независимо от этих физических причин, большие возмущения, изменяющие исходную систему на какое-то время и нарушающие ее исходный режим, или малые возмущения, которые появляются во время нормальной работы системы. Градация ПП по допущениям сделанным при математическом их описании, особенно разнообразна, поэтому ограничиваются только наиболее существенными признаками. Например, анализ реальной нелинейной системы может проводиться при учете имеющихся нелинейностей или замене нелинейных зависимостей параметров режима линейными. По линеаризованным уравнениям проводятся как исследования статической устойчивости, так и исследования, связанные с оценкой показателей качества ПП. По нелинейным уравнениям проводятся исследования динамической и результирующей устойчивости и ПП после больших возмущений. Ряд допущений, принимаемых при исследованиях эл.мех-х ПП, основывающихся на методах электротехники, механики, теории колебаний, имеет свои существенные особенности. Например, при рассмотрении электричесих систем переменного тока можно оперировать мгновенными значениями тока и напряжения и составлять применительно к ним уравнения. Важные допущения, принимаемые при анализе эл.мех-х ПП, касаются учета изменений скорости роторов СМ, реакции якоря в них и электромагнитных процессов в АМ. При процессах, связанных с синусоидальными изменениями параметров режима основной рабочей частоты (50 Гц), обычно рассматриваются не мгновенные значения, а их огибающие. Анализ, проводимый без этого упрощения, называется или анализом по полным уравнениям с учетом влияния изменения мгновенных значений, или анализом в мгновенных значениях, или анализом по уравнениям Парка-Горева. При расчете по огибающим изменения электрической мощности принимаются происходящими мгновенно. Все упрощения анализа ПП заключаются в выделении главного, практически существенного для решения поставленных задач. Одним из упрощающих приемов, широко применяемых при анализе ПП, является замена реальных динамических характеристик элементов электрических систем их статическими характеристиками, а также рассмотрение динамической электрической системы как системы позиционной (позиционная система – это система, энергия которой есть функция от состояния).
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 459; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.52.182 (0.144 с.) |


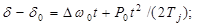
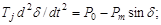


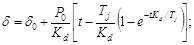




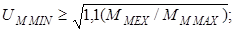
 Для больших качаний в отличие от асинхронного хода характерен провал в зависимости P=f(t) появляющийся при переходе угла за 90°. Для асинхронного хода характерно именно периодическое изменение знака синхронной мощности (рис. 14.1, в).
Для больших качаний в отличие от асинхронного хода характерен провал в зависимости P=f(t) появляющийся при переходе угла за 90°. Для асинхронного хода характерно именно периодическое изменение знака синхронной мощности (рис. 14.1, в).