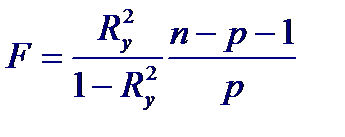Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анализ коэффициента корреляцииСодержание книги Поиск на нашем сайте
Максимально правдоподобная оценка коэффициента корреляции, получаемая на основе n пар нормально распределенных случайных величин (xi, yi), i = 1,… n, имеет вид
Если экспериментальные данные сгруппированы по одной или обеим переменным, то расчетная формула изменяется соответствующим образом. Например, если данные сгруппированы по значениям X, т. е. среди xi есть повторяющиеся значения Y, то
Где
При достаточно большом объеме выборки (n ≥ 50) и небольших значениях коэффициента корреляции (r 2 << 1) оценка коэффициента корреляции близка к нормальному распределению с математическим ожиданием равным истинному значению r. Тогда для доверительной вероятности β = 1− α получим следующее выражение для доверительного интервала:
где z1− α /2 – квантиль порядка 1− α /2 стандартного нормального распределения.
Случайная величина v уже при небольших n (n ≥ 20) приблизительно распределена по нормальному закону с параметрами:
распределена по нормальному закону с нулевым математическим ожиданием и единичной дисперсией, а доверительный интервал для M [ v ] будет иметь вид
можно получить доверительный интервал для коэффициента корреляции.
которая при справедливости нулевой гипотезы распределена по закону Стьюдента с n −2 степенями свободы. При альтернативной гипотезе H1: r ≠ 0 нулевая гипотеза отвергается с уровнем значимости α, если
37. Оценка степени тесноты связи при нелинейной зависимости При отклонении исследуемой зависимости от линейной, коэффициент корреляции r теряет свой смысл как характеристика тесноты связи. В этих случаях необходимо попытаться построить по имеющимся выборочным данным оценку корреляционного отношения.
Тогда оценкой среднего значения Y внутри каждого интервала будет
Точечной оценкой общей (полной) дисперсии D [ Y ], характеризующей разброс результатов наблюдений yij относительно общего среднего будет
Тогда получим следующее выражение для точечной оценки квадрата корреляционного отношения ρ 2 yx зависимой переменной Y по независимой переменной X:
Аналогично можно ввести точечную оценку ρ 2 xy
которая при справедливости гипотезы имеет распределения Фишера с m −1 и n − m степенями свободы. Поэтому, если вычисленное значение статистики F окажется больше fm −1; n − m; α (α - процентной точки), то нулевую гипотезу следует отвергнуть с уровнем значимости α, т. е. признать, что связь существует. Для истинного значения квадрата корреляционного отношения ρ 2 yx можно построить приближенный доверительный интервал с доверительной вероятностью β =1- α:
38. Анализ частных связей. Анализ множественных связей Анализ частных связей При анализе корреляционных связей могут возникнуть трудности в интерпретации полученных результатов. Полученная сильная корреляционная связь входит в противоречие со здравым смыслом. Подобная ситуация возникает при опосредованном влиянии на оба изучаемых показателя третьего неизвестного фактора и даже целого множества неучтенных факторов. Поэтому необходимо введение таких измерителей статистической связи, которые были бы очищены от влияния других переменных, т. е. давали бы оценку степени тесноты связи при условии, что остальные переменные зафиксированы на некотором постоянном уровне. В этом случае говорят об анализе частных связей и используют частные коэффициенты корреляции.
где rij – коэффициенты корреляции между случайными величинами xi и xj; i, j = 0, 1...., p.
где Aij – алгебраическое дополнение к элементу rij корреляционной матрицы, а J (i, j) = 0, 1...., p за исключением индексов i и j. Например, для трех случайных величин X 0, X 1, X 2 получим корреляционную матрицу вида
Значения точечных оценок частных коэффициентов корреляции получают подстановкой в выражения их выборочных значений. Выборочный частный коэффициент корреляции распределен так же, как и выборочный обычный (парный) коэффициент корреляции, поэтому для проверки гипотез и построения доверительного интервала используются те же самые соотношения, которые были получены ранее с единственной заменой n на n − k, где k – порядок частного коэффициента корреляции (число “ мешающих ” переменных). Анализ множественных связей Оценка степени тесноты связи между входной переменной Y и входными переменными X 1, X 2,..., Xp, осуществляется с помощью множественного коэффициента корреляции Ry. Величина Ry2 показывает, какая доля от полной дисперсии D [ Y ] результирующей переменой Y определяется контролируемым нами изменением функции φ (X 1, X 2,..., Xp):
Для проверки нулевой гипотезы H0: Ry2 = 0 используют статистику:
которая при справедливости гипотезы H0 имеет распределение Фишера с р и n − p −1 степенями свободы. Гипотеза об отсутствии множественной корреляционной связи между Y и X отвергается с уровнем значимости α, если расчетное значение статистики F превышает α-процентную точку распределения Фишера р и n − p −1 степенями свободы.
39. Ранговые коэффициенты корреляции Если необходимо исследовать двумерные данные, закон распределения которых заметно отличается от нормального, то для решения вопроса о некоррелированности или коррелированности этих данных нельзя применять критерии проверки гипотез о значимости коэффициента корреляции, рассмотренные ранее. В этом случае можно воспользоваться методом, основанным на рангах наблюдений каждой переменной и приводящим к коэффициентам ранговой корреляции.
|
|||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 307; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.68.112 (0.01 с.) |

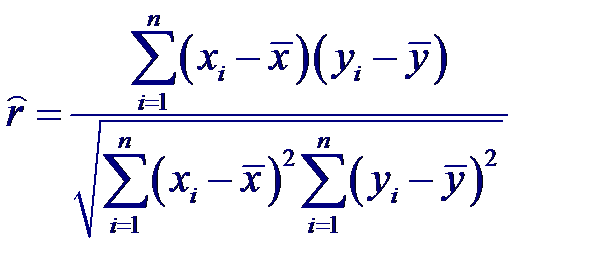
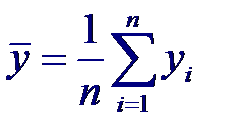
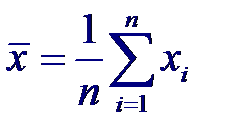 где
где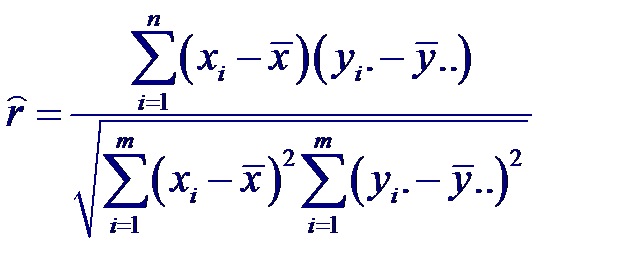
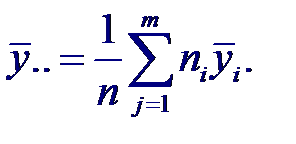
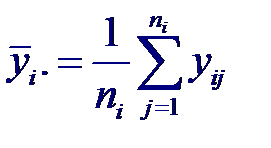
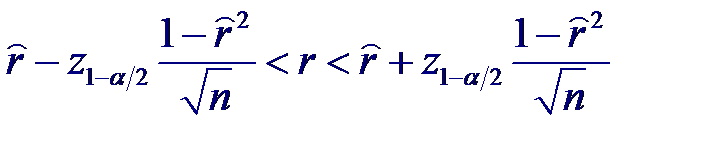
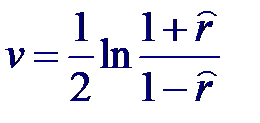 Для выборок небольших объемов (n < 50) и значениях |r| близких к единице распределение оценки коэффициента корреляции существенно отличается от нормального. В этом случае Фишер предложил использовать следующее преобразование над оценкой коэффициента корреляции, приводящей к новой случайной величине v:
Для выборок небольших объемов (n < 50) и значениях |r| близких к единице распределение оценки коэффициента корреляции существенно отличается от нормального. В этом случае Фишер предложил использовать следующее преобразование над оценкой коэффициента корреляции, приводящей к новой случайной величине v: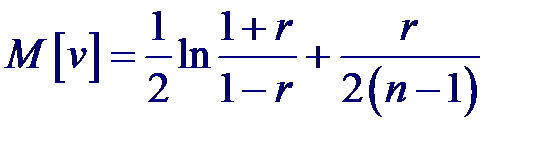
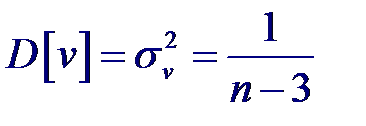
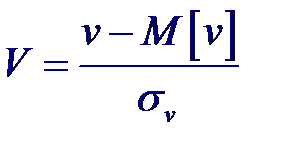 Тогда статистика
Тогда статистика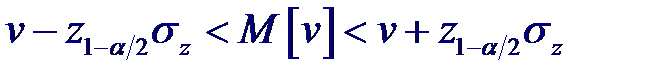
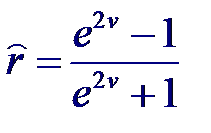 Применив обратное преобразование Фишера
Применив обратное преобразование Фишера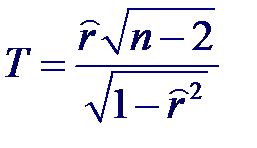 Задача проверки некоррелированности (а значит и независимости) совместно нормальных случайных величин сводится к проверке гипотезы H0: r = 0. Статистикой критерия проверки такой гипотезы является случайная величина
Задача проверки некоррелированности (а значит и независимости) совместно нормальных случайных величин сводится к проверке гипотезы H0: r = 0. Статистикой критерия проверки такой гипотезы является случайная величина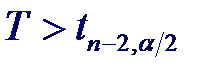
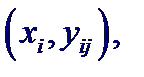 Предположим, что характер выборки (количество элементов, плотность расположения на плоскости) допускает группировку по переменной X, т. е. данные могут быть представлены в виде
Предположим, что характер выборки (количество элементов, плотность расположения на плоскости) допускает группировку по переменной X, т. е. данные могут быть представлены в виде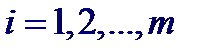
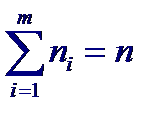
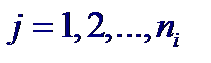
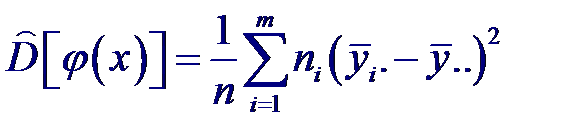 За значение точечной оценки величины D [ ϕ (X)], обусловливающей вклад в общую дисперсию D [ Y ] случайной величины Y от функциональной зависимости, принимают
За значение точечной оценки величины D [ ϕ (X)], обусловливающей вклад в общую дисперсию D [ Y ] случайной величины Y от функциональной зависимости, принимают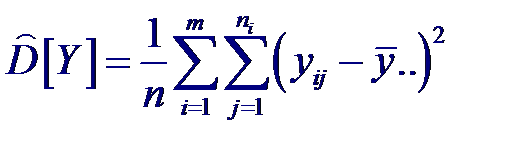
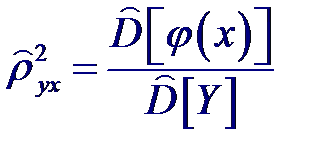
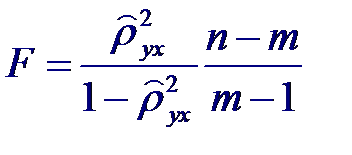 В предположении, что при условии X = x случайная величина Y имеет нормальный закон распределения с постоянной дисперсией для любого x, для проверки гипотезы H0: ρ 2 yx = 0 (отсутствие связи Y с X) используется статистика
В предположении, что при условии X = x случайная величина Y имеет нормальный закон распределения с постоянной дисперсией для любого x, для проверки гипотезы H0: ρ 2 yx = 0 (отсутствие связи Y с X) используется статистика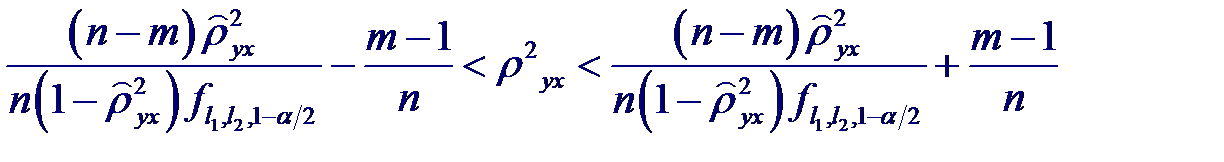
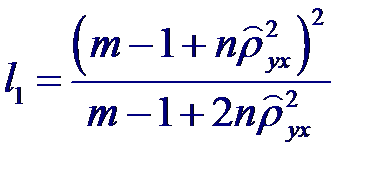 где l 1 и l 2 – числа степеней свободы:
где l 1 и l 2 – числа степеней свободы: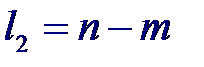
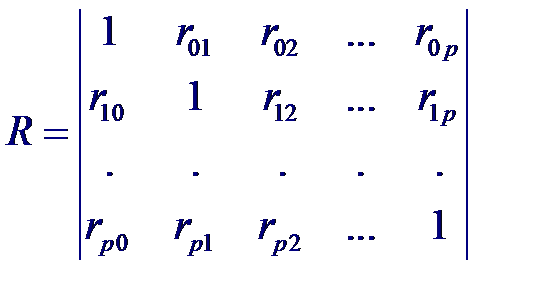 Рассмотрим статистические связи между совокупностью р +1 случайных величин X 0, X 1,..., Xp где переменные X 1,..., Xp являются входными, а переменная X 0 = Y –выходной. Предположим, что случайный вектор (X 0, X 1,..., Xp) имеет нормальный закон распределения. Тогда корреляционная матрица будет иметь вид:
Рассмотрим статистические связи между совокупностью р +1 случайных величин X 0, X 1,..., Xp где переменные X 1,..., Xp являются входными, а переменная X 0 = Y –выходной. Предположим, что случайный вектор (X 0, X 1,..., Xp) имеет нормальный закон распределения. Тогда корреляционная матрица будет иметь вид: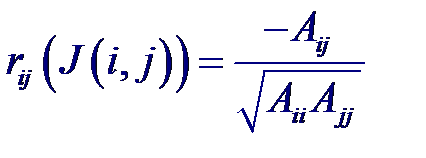 Частный коэффициент корреляции – мера линейной вероятностной зависимости между двумя случайными величинами из некоторой совокупности случайных величин X 0, X 1,..., Xp, когда исключено влияние остальных, т. е. (для пары Xi и Xj)
Частный коэффициент корреляции – мера линейной вероятностной зависимости между двумя случайными величинами из некоторой совокупности случайных величин X 0, X 1,..., Xp, когда исключено влияние остальных, т. е. (для пары Xi и Xj)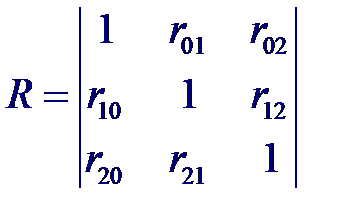
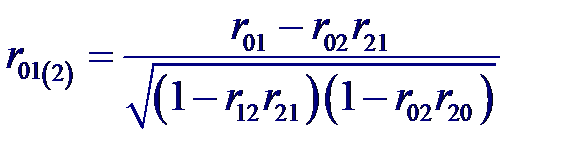 и частный коэффициент корреляции между входной переменной X 0 и выходной X 1 при фиксированном значении переменной X 2
и частный коэффициент корреляции между входной переменной X 0 и выходной X 1 при фиксированном значении переменной X 2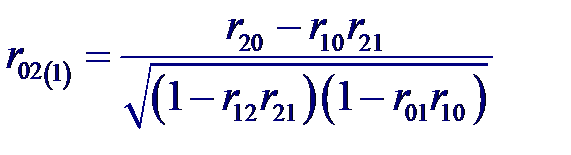 и частный коэффициент корреляции между входной переменной X 0 и выходной X 2 при фиксированном значении переменной X 1
и частный коэффициент корреляции между входной переменной X 0 и выходной X 2 при фиксированном значении переменной X 1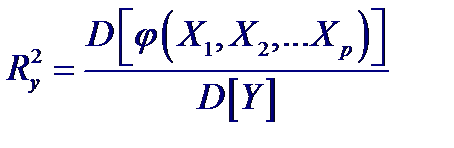
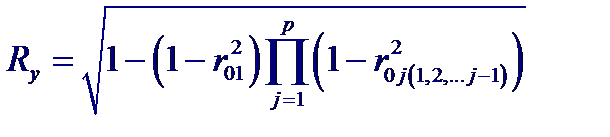 Значение множественного коэффициента корреляции Ry можно вычислить, используя частные коэффициенты корреляции, следующим образом:
Значение множественного коэффициента корреляции Ry можно вычислить, используя частные коэффициенты корреляции, следующим образом: