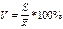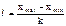Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графический метод статистики является дополнением табличного метода.Содержание книги
Поиск на нашем сайте
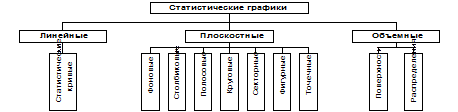
СТАТИСТИЧЕСКИЕ ГРАФИКИ График – чертеж, на котором при помощи условных геометр. фигур изображаются стат. данные. В результате этого достигается наглядная хар-ка изучаемой стат. совокупности. Правильно построенный график делает стат. информацию более выразительной, запоминающейся и удобно воспринимаемой.
Графики в статистике имеют не только иллюстративное значение, они позволяют получить доп. знания о предмете исследования, к-рые в цифровом варианте остаются скрытыми. Любое стат. исследование на основе какого-либо метода в конечном итоге дополняется использованием графического метода.
Знак Варзара. Варзар предложил использовать прямоугольные фигуры для графического изображения трех показателей, один из которых является произведением двух других. В каждом таком прямоугольнике основание пропорционально одному из показателей — сомножителей, а высота его соответствует второму показателю. Площадь прямоугольника равна величине третьего показателя, являющегося произведением двух первых. Располагая рядом несколько прямоугольников, относящихся к разным показателям, можно сравнивать не только размеры показателя — произведения, но и значения показателей — сомножителей. ОСНОВНЫЕ ПРАВИЛА В общем расположении на поле графических образов они размещаются слева направо. При этом масштабные ориентиры графика по горизонтальной шкале, как правило, размещаются от его нижней части. Для вертикальной шкалы масштабные ориентиры обычно размещаются в левой части графика. В график по возможности следует включать исходные данные. Если это нецелесообразно, то исходные данные должны в табличной форме сопровождать график. Все буквенные и цифровые значения должны располагаться на графике так, чтобы их легко можно было отсчитать от начала масштабной шкалы. Ряды цифровых данных, отображающие изменения показателей коммерческой деятельности во времени, размещаются в строгой хронологической последовательности и обязательно по оси абсцисс. Общим требованием графического метода является то, что факторные признаки размещаются на горизонтальной шкале графика и их изменения читаются слева направо, а результативные признаки — по вертикальной шкале и читаются снизу вверх. При этом важно, чтобы заголовок графика был бы кратким, но достаточно четко пояснял основное его содержание.
Абсолютные и относительные величины. Абсолютные стат. величины показывают объем, размеры, уровни различных социально-экономических явлений и процессов. Отражают уровни в физических мерах объема, веса и т.п. В общем абсолютные стат. величины – это именованные числа. Они всегда имеют определенную размерность и единицы измерения. Последние определяют сущность абсолютной величины. Типы абсолютных величин Натуральные – такие единицы, которые отражают величину предметов, вещей в физических мерах. Денежные (стоимостные) – используются для характеристики многих экономических показателей в стоимостном выражении. Трудовые – используются для определения затрат труда (человеко-час, человеко-день). Условно-натуральные – единицы, к-рые используются для сведения воедино нескольких разновидностей потребительных стоимостей. Виды абсолютных величин Индивидуальные – отражают размеры количественных признаков у отдельных единиц изучаемой совокупности. Общие – выражают размеры, величину количественных признаков у всей изучаемой совокупности в целом. Абсолютные величины отражают наличие тех или иных ресурсов, это основа материального учета. Они наиболее объективно отражают развитие экономики и являются основой для расчета разных относительных стат. показателей. Относительные стат. величины выражают количественные соотношения м/у явлениями общественной жизни, они получаются в результате деления одной абсолютной величины на другую. Знаменатель (база) – это величина, с к-рой производится сравнение. Сравниваемая величина – это величина, к-рая сравнивается. Относительная величина показывает, во сколько раз сравниваемая величина больше или меньше базисной или какую долю первая составляет по отношению ко второй. В ряде случае относительная величина показывает, сколько единиц одной величины приходится на единицу другой. Важное свойство – относительная величина абстрагирует различия абсолютных величин и позволяет сравнивать такие явления, абсолютные размеры которых непосредственно несопоставимы.
В результате сопоставления одноименных абсолютных величин получают неименованные относительные величины. Они могут выражаться в виде долей, кратных соотношений, процентных соотношений и т.д. Результатом сопоставления разноименных величин являются именованные относительные величины. Их название образуется сочетанием сравниваемой и базисной абсолютных величин. Выбор формы зависит от характера аналитической задачи, которая состоит в том, чтобы с наибольшей ясностью выразить соотношение.
Средняя величина – это обобщающий показатель, характеризующий однотипные общественные явления по одному количественному признаку в конкретных условиях места и времени. Например, ср/месяч. з/п, средняя продолжительность жизни, средняя урожайность. Средняя показывает уровень признака отнесенный к единице совокупности. Например, средняя урожайность, средняя заработная плата, среднее количество выпавших осадков, средняя продолжительность жизни и т.д. Сравнивая во времени изменение средних уровней в одних и тех же совокупностях, ст. тем самым определяет закономерности развития социально-экономических явлений, т.е. в этих изменениях проявляется общая тенденция (типичность) развития явления. Первым условием применения средних величин является тот факт, что все средние должны опираться на массовые общественные явления. Вторым условием применения средних является тот факт, что групповые средние должны дополняться общими средними (ср. урожайность пшеницы в Орловской области и средняя урожайность в РФ). Третьим условием является то, что все показатели средних должны определяться по однородной совокупности. Обычно средние показатели ст. определялись как среднее арифметическое в том случае, когда были указаны индивидуальные значения признака. Если в совокупности признаки имеют частоту повторения (вес), то в этом случае среднее арифметическое принимало форму взвешенной, т.о. среднее рассчитывается в виде арифметической, но в форме простой и взвешенной. Например, з/п 5 рабочих составляет 400, 420, 480, 510, 550. Чтоб определить среднюю з/п 1 рабочего, нужно сложить все показатели и разделить на 5.
Средняя арифметическая простая равна сумме показателей (уровней), деленной на число показателей (уровней). Средняя арифметическая взвешенная принимается в тех случаях, когда известны отдельные значения признака и их веса (fi), т.е. частота повторения признака.
Средняя арифметическая взвешенная равна сумме произведений признака на вес, деленной на сумму веса. В этой формуле числитель дроби выражает прямую зависимость в результате чего, получается реальный экономический смысл. Например, количество рабочих перемноженное на среднемесячную з/п одного рабочего в конечном итоге представляет собой фонд з/п. Если показатель будет представлен в виде интервала (з/п в 400-500, 500-600, 600-700…), то при расчетах средней необходимо определить середину интервала по средней арифметической простой, а затем производить последующий расчет. В расчетах средней арифметической взвешенной применяются следующие методы (приемы): 4. Если значение X уменьшить в одно и то же число раз, то занчение средней увеличится в это же число раз.
4. Если значение X увеличить в одно и то же количество раз, то значение средней уменьшится это же количество раз; 5. Если все значения веса f изменить в несколько раз, то значение средней не изменится. Если для решения задачи используется 3 метода (приема), то эта задача решена способом моментов. Вторым видом средних величин является средняя гармоническая, которая применяется в двух формах: простой и взвешенной. Средняя гармоническая применяется в тех случаях, когда известно отдельные значения признака X и объемы признаков. Объемом может быть: фонд з/п, валовой сбор, сумма товарооборота, стипендиальный фонд, фактический выпуск продукции. В этой формуле наблюдается обратная связь, т.е. при делении 2-ух показателей получается 3 имеющий экономический смысл. Например, при делении фактического товарооборота на количество проданных товаров мы получим цену товара. Формула средней гармонической простой:
Эта формула обратная средней арифметической простой и предполагается, что сумма объемов в данном случае равна единице. Средняя гармоническая взвешенная:
Средняя гармоническая взвешенная равна сумме объемов признаков деленная на сумму отношения объема к признаку. Средняя квадратическая:
Средняя кубическая:
средняя хронологическая. средняя геометрическая;
Мода - это величина признака (варианта), наиболее часто повторяющаяся в изучаемой совокупности. Для дискретных рядов распределения модой будет значение варианта с наибольшей частотой. где
Медиана - это варианта, расположенная в середине вариационного ряда. Если ряд распределения дискретный и имеет нечетное число членов, то медианой будет варианта, находящаяся в середине упорядоченного ряда.
где
Для хар-ки колеблемости признака используется ряд показателей. Наиболее простой из них - Размах вариации - разность м/у Чтобы дать обобщающую хар-ку распределению отклонений, исчисляют среднее линейное отклонение d, к-рое учитывает различие всех единиц изучаемой совокупности.
Ср. лин. откл. опр. как средняя арифмет. из отклонений индивидуальных значений от средней, без учета знака этих отклонений: простое Дисперсия - это средняя арифметич. квадратов отклонений каждого значения признака от общей средней. В зависимости от исходных данных дисп. может вычисляться по средней арифметич. простой Среднее квадратическое отклонение - это обобщающая хар-ка абсолютных размеров вариации признака в совокупности. Чем меньше ср. квадр. откл., тем лучше средняя арифметич. отражает собой всю совокупность. Коэфф. осцилляции отражает относит. колеблемость крайних значений признака вокруг средней: Относит. лин. откл. хар-ет долю усредненного значения абсолютных отклонений от средней величины. Коэффициент вариации:
27. Характеристика и закономерности рядов распределения Ряды распределения. Проведение вариационного анализа начинается с построения вариационного ряда – упорядоченное распределение единиц совокупности по возрастающим или по убывающим признакам и подсчет соответствующих частот. Ряды распределения: 1. Ранжированный вариационный ряд – перечень отдельных ед. совокупности в порядке возрастания убывания ранжированного признака; 2. Дискретный вариационный ряд – таблица, состоящая из 2х строк – полимерных значений варьирующего признака и кол-во единиц с данным значением признака. 3. Интервальный вариационный ряд строится в случаях: *признак принимает дискретные значения, но кол-во их слишком велико; *признака принимает любые значения в определенном диапазоне. При построении интервального вариационного ряда необходимо выбрать оптимальное количество групп, самый распространенный способ по формуле Стерджесса k=1+3.32lgn, где k – количество интервалов; n – объем совокупности. При расчетах почти всегда получают дробные значения, округления производить до целого числа. Длина интервала – l
Выборочное наблюдение представляет собой один из наиболее широко применяемых видов несплошного наблюдения. При проведении выборочного наблюдения, изучают не все единицы изучаемого объекта, или иными словами, обследуются не все единицы генеральной совокупности, а лишь некоторая отобранная часть единиц. Наблюдение организованно т.о., что эта часть отобранных единиц в уменьшенном масштабе репрезентирует (представляет) всю совокупность. Часть единиц генеральной совокупности, подлежащая непосредственному наблюдению, называется выборочной совокупностью. Система отбора единиц и способов характеристики изучаемой совокупности составляет основу выборочного метода. В расчетах выборочного метода рассматривается следующие показатели Средняя дисперсия СКО (среднеквадратичное отклонение); Теория вероятности; Рассматривая подробно показатели выборочного метода, можно обнаружить ошибки, которые представляют собой ошибки регистрации и ошибки репрезентативности. По виду отбора различают индивидуальный, групповой и комбинированный отбор. При индивидуальном отборе в выборочной совокупности отбираются отдельные единицы совокупности. При групповом отборе – качественно-однородные группы или серии изучаемых единиц. В комбинированном отборе происходит сочетание первого и второго отбора.
По методу отбора выборка делится на повторную и бесповторуную. При повторной выборке количество единиц остается постоянным, т.е. при выборке рассматриваются все единицы и в генеральную совокупность после регистрации попадают те же самые единицы. По типу возвращающего шара, т.е. при повторном отборе прежде выбранная единица рассматривается и попадает в генеральную совокупность несколько раз. При бесповторной выборке единиц совокупности попавшая в выборку единица не возвращается в генеральную совокупность, т.е. в дальнейшей выборке она не участвует. И последующую выборку делают из генеральной совокупности уже без отобранных ранее единиц (не возвращающийся шар). Численность единиц в генеральной совокупности при исследовании сокращается. По степени охвата единиц совокупности различают большую и малую выборку. При малой выборке количество отобранных единиц всегда <30. Схема выборки:
В практике выборочных наблюдений в зависимости от видов отбора получают следующие формы организации выборочного наблюдения: Собственно-случайная; Механическая; Типическая; Серийная; Комбинированная; При выборочном наблюдении должна быть обеспечена случайность отбора единиц. Каждая единица должна иметь равную возможность быть отобранной. Именно в этом и заключается собственно-случайная выборка, при которой отбор единиц из генеральной совокупности без предварительного расчленения на группы посредством жеребьевки или с помощью единиц отбора по таблицам случайного отбора производится выбор параметров средних, абсолютных и относительных показателей. Примером собственно-случайной выборки может служить лотерея, когда из общего количества выпущенных билетов наугад отбирается часть номеров, на которые приходятся выигрыши. При этом количество отобранных единиц в выборочной совокупности обычно определяется из доли выборки. Доля выборки представляет собой отношение числа единиц выборочной совокупности к общему числу генеральной совокупности. Например, при 5% выборке из партии деталей в 1000 единиц объем выборки или доля составят 50 единиц. В чистом виде такая форма выборочного наблюдения встречается редко, но она является исходной среди других форм отбора, а также в ней заключаются основные принципы выборочного наблюдения. Механическая – отбор единиц в выборочную совокупность производится из генеральной совокупности, разбитой на равные интервалы (группы). При этом размер интервала в генеральной совокупности равно обратной величине доли выборки. Так, при 2%-ой выборки выбирается каждая 50 единица (1:0,02), при 5%-й – каждый 20 единица и т.д. Т.о., в соответствии с принятой долей отбора генеральная совокупность как бы механически разбивается на равновеликие группы. Из каждой такой группы в выборку отбирается лишь одна единица. При типич. выборке генеральная совокупность вначале расчленяется на однородные типич. группы. Затем из каждой типич. группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность. Типич. выборка обычно применяется при изучении сложной статистической совокупности. Например, при выборочном обследовании производительности труда работников торговли, состоящих из отдельной группы по квалификации. При серийной выборке из генеральной совокупности отбирается не отдельные единицы, а целые их серии (гнезда). Внутри по каждой из попавших в выборку серий обследуются все без исключения единицы, т.е. применяется сплошное наблюдение. Применение серийной выборки в торговле обусловлено тем, что многие товары для их транспортировки, хранения и продажи, упаковываются в пачки. Поэтому при контроле качества рационально проверить отдельных упаковок. Комбинированная выборки может быть двух ступенчатой. При этом генеральная совокупность сначала разбивается на группы. Затем производит отбор групп, а внутри последних осуществляется отбор отдельных единиц. Выборка может быть многоступенчатой.
Ошибка выборки — это объективно возникающее расхождение между характеристиками выборки и генеральной совокупности. Она зависит от ряда факторов: степени вариации изучаемого признака, численности выборки, методом отбора единиц в выборочную совокупность, принятого уровня достоверности результата исследования.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 243; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.104.198 (0.012 с.) |


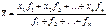

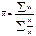 ;
; 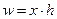
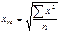
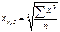
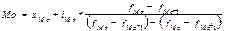
 - начальное значение интервала, содержащего моду;
- начальное значение интервала, содержащего моду;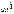 - величина модального интервала;
- величина модального интервала; - частота модального интервала;
- частота модального интервала; - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному; - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным.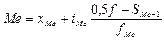
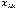 — начальное значение интервала, содержащего медиану;
— начальное значение интервала, содержащего медиану; — величина медианного интервала;
— величина медианного интервала; — сумма частот ряда;
— сумма частот ряда; — сумма накопленных частот, предшествующих медианному интервалу;
— сумма накопленных частот, предшествующих медианному интервалу; — частота медианного интервала.
— частота медианного интервала.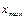 и
и  знач-ми вариантов.
знач-ми вариантов. 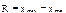
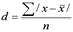 взвешенное
взвешенное 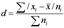 .
. или взвешенной
или взвешенной 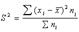
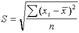 .
.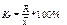
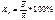 .
.