
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непозиционные системы счисленияСодержание книги
Поиск на нашем сайте
В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе. При этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания. В биномиальной системе счисления (англ.) число x представляется в виде суммы биномиальных коэффициентов:
При всяком фиксированном значении Система остаточных классов (СОК) Представление числа в системе остаточных классов основано на понятии вычета и китайской теореме об остатках. СОК определяется набором попарно взаимно простых модулей
…
В СОК арифметические операции (сложение, вычитание, умножение, деление) выполняются покомпонентно, если про результат известно, что он является целочисленным и также лежит в
Двоичная, восьмеричная, шестнадцатеричная системы счисления Двоичная система счисления Для представления чисел в микропроцессоре используется двоичная система счисления. x = an·2n+an-1·2n-1+...+a1·21+a0·20+a-1·2-1+a-2·2-2+...+a-m·2-m где ai - двоичные цифры (0 или 1). В восьмеричной системе счисления базисными цифрами являются цифры от 0 до 7. 8 единиц младшего разряда объединяются в единицу старшего. В шестнадцатеричной системе счисления базисными цифрами являются цифры от 0 до 15 включительно. Для обозначения базисных цифр больше 9 одним символом кроме арабских цифр 0…9 в шестнадцатеричной системе счисления используются буквы латинского алфавита: 1010 = A16 1210 = C16 1410 = E16 Например, число 17510 в шестнадцатеричной системе счисления запишется как AF16. Действительно, 10·161+15·160=160+15=175 В таблице представлены числа от 0 до 16 в десятичной, двоичной, восьмеричной и шестнадцатеричной системах счисления.
Перевод чисел в различные системы счисления Для перевода числа из десятичной системы счисления в систему счисления с другим основанием поступают следующим образом: а) Для перевода целой части числа его делят нацело на основание системы, фиксируя остаток. Если неполное частное не равно нулю продолжают делить его нацело. Если равно нулю остатки записываются в обратном порядке. б) Для перевода дробной части числа ее умножают на основание системы счисления, фиксируя при этом целые части полученных произведений. Целые части в дальнейшем умножении не участвуют. Умножение производиться до получения 0 в дробной части произведения или до заданной точности вычисления. в) Ответ записывают в виде сложения переведенной целой и переведенной дробной части числа. Для перевода числа в десятичную систему счисления из системы счисления с другим основанием каждый коэффициент переводимого числа умножается на основание системы в степени соответствующей этому коэффициенту и полученные результаты складываются. Пример: перевод чисел из двоичной системы счисления в десятичную систему счисления Перевести число 1001011,0112 в десятичную систему счисления 1001011,0112 = 1*26+0*25+0*24+1*23+0*22+1*21+1*20+0*2-1+1*2-2+1*2-3 =64+8+2+1+0,25+0,125=75,375 Для перевода из двоичной системы счисления в восьмеричную необходимо разбить данное двоичное число вправо и влево от запятой на триада (три цифры) и представить каждую триаду соответствующим восьмеричным кодом. При невозможности разбиения на триады допускается добавление нулей слева в целой записи числа и справа в дробной части числа. Для обратного перевода каждую цифру восьмеричного числа представляют соответствующей триадой двоичного кода. Правило перевода из двоичной системы счисления в шестнадцатеричную: разбить двоичное число вправо и влево от запятой на тетрады (по 4 цифры) и представить каждую тетраду соответствующим шестнадцатеричным кодом. При невозможности разбиения на тетрады допускается добавление нулей слева в целой записи числа и справа в дробной части числа. Для обратного перевода каждую цифру шестнадцатеричного числа представляют тетрадой двоичного кода.
6 Принципы фон Неймана Архитектура фон Неймана — широко известный принцип совместного хранения команд и данных в памяти компьютера. Вычислительные системы такого рода часто обозначают термином «машина фон Неймана», однако соответствие этих понятий не всегда однозначно. В общем случае, когда говорят об архитектуре фон Неймана, подразумевают принцип хранения данных и инструкций в одной памяти. Принципы фон Неймана Принцип однородности памяти Команды и данные хранятся в одной и той же памяти и внешне в памяти неразличимы. Распознать их можно только по способу использования; то есть одно и то же значение в ячейке памяти может использоваться и как данные, и как команда, и как адрес в зависимости лишь от способа обращения к нему. Это позволяет производить над командами те же операции, что и над числами, и, соответственно, открывает ряд возможностей. Так, циклически изменяя адресную часть команды, можно обеспечить обращение к последовательным элементам массива данных. Такой прием носит название модификации команд и с позиций современного программирования не приветствуется. Более полезным является другое следствие принципа однородности, когда команды одной программы могут быть получены как результат исполнения другой программы. Эта возможность лежит в основе трансляции — перевода текста программы с языка высокого уровня на язык конкретной вычислительной машины. Принцип адресности Структурно основная память состоит из пронумерованных ячеек, причем процессору в произвольный момент доступна любая ячейка. Двоичные коды команд и данных разделяются на единицы информации, называемые словами, и хранятся в ячейках памяти, а для доступа к ним используются номера соответствующих ячеек — адреса.
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 334; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.145.41 (0.007 с.) |

 , где
, где 
 каждое натуральное число представляется уникальным образом.
каждое натуральное число представляется уникальным образом.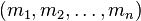 с произведением
с произведением  так, что каждому целому числу
так, что каждому целому числу  из отрезка
из отрезка  ставится в соответствие набор вычетов
ставится в соответствие набор вычетов  , где
, где
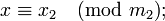

 .
.


