
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кванторы и квантификация. Специфика фрактальной квантификацииСодержание книги
Поиск на нашем сайте
Впервые понятие " квантор" ввелв математическую логику Чарльз Пирс[7]. Первоначально это понятие было связано с логикой предикатов, что отразилось на его исходном определении. Слово " квантор" происходит от лат. quantum – "сколько", "количество"[8]. В рамках логики предикатов кванторы – это общее название логических операций, которые по предикату Наиболее употребительны квантор всеобщности Если интересуются поведением предиката В более общем смысле кванторы - это операторы математической логики, применяемые к логическим выражениям и дающие характеристику области предметов или области предикатов, к которой относится данное логическое выражение. В рамках разрабатываемой трехзначной фрактальной логики мы вводим в рассмотрение два новых квантора: · квантор фрактальной фазификации, · квантор фрактальной дефазификации.
Введение квантора фрактальной фазификации в математический инструментарий этой логики связано с генерацией двух фракталов (фрактальных множеств) с нечеткими величинами: · фрактала значений предметной переменной, · фрактала значений функции принадлежности.
Реализацию квантора фрактальной фазификации мы свяжем с процедурой, выполняемой на основе разработанной нами модели рекурсивного итерируемого процесса, сущность и схема которого будут показаны ниже. А реализацию второго квантора – квантора фрактальной дефазификации – свяжем с процедурой определения центров тяжести для двух порожденных фрактальных множеств – фрактала значений предметной переменной и соответствующего ему фрактала значений истинности. В шутку, мы называем эти фракталы "зоопарками" – " зоопарком" значений предметных переменных и " зоопарком" значений функции принадлежности.
Формально любая из операций над двумя нечеткими множествами
Более компактно, со скобками, устанавливающими порядок выполнения действий, этот кортеж можно записать так:
· · · · · · [ В результате выполнения итерационного процесса формируются два фрактала значений: · · Операция фрактальной дефазификации
где
Раскроем вид оператора
|
||||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 250; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.105.80 (0.006 с.) |

 строят высказывание, дающее количественную характеристику области истинности предиката
строят высказывание, дающее количественную характеристику области истинности предиката  ("для всех
("для всех 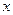 ") и квантор существования
") и квантор существования  ("для некоторых
("для некоторых  означает, что, область истинности предиката
означает, что, область истинности предиката  означает, что область истинности предиката
означает, что область истинности предиката  , то часто употребляют так называемые ограничительные кванторы
, то часто употребляют так называемые ограничительные кванторы 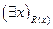 и
и  , при этом высказывание
, при этом высказывание  означает то же, что и
означает то же, что и  , а высказывание
, а высказывание  - то же, что
- то же, что  , где
, где 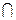 - знак конъюнкции, а
- знак конъюнкции, а  - знак импликации.
- знак импликации. и
и  из нечеткой трехзначной логики может быть преобразована в кортеж операций (упорядоченную 3-ку) нечеткой фрактальной логики. Этот кортеж состоит их цепочки операторов: “
из нечеткой трехзначной логики может быть преобразована в кортеж операций (упорядоченную 3-ку) нечеткой фрактальной логики. Этот кортеж состоит их цепочки операторов: “ 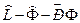 ”, где:
”, где: - оператор логической операции нечеткой трехзначной логики
- оператор логической операции нечеткой трехзначной логики - оператор квантора фрактальной фазификации
- оператор квантора фрактальной фазификации - оператор квантора фрактальной фазификации
- оператор квантора фрактальной фазификации  , где:
, где: - верхняя граница - максимальное число итераций в процессе генерации фракталов;
- верхняя граница - максимальное число итераций в процессе генерации фракталов; - нижняя граница – исходное, начальное состояние (перед выполнением итерационного процесса);
- нижняя граница – исходное, начальное состояние (перед выполнением итерационного процесса); - индекс
- индекс 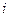 - индекс
- индекс  и
и 
 -предметная переменная нечетких множеств
-предметная переменная нечетких множеств  и
и  для
для  , где
, где  - мнимая компонента – волатильность
- мнимая компонента – волатильность  - мнимая единица.
- мнимая единица. ,
,  ,
, 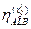 ] – кортеж значений истинности функции принадлежности
] – кортеж значений истинности функции принадлежности  , получаемый после выполнения операции
, получаемый после выполнения операции  - " зоопарк" значений предметных переменных и
- " зоопарк" значений предметных переменных и - " зоопарк" значений функции принадлежности.
- " зоопарк" значений функции принадлежности. и
и  ,
, и
и  .
. и
и  . Эти операции должны выполняться до начала итерационного процесса
. Эти операции должны выполняться до начала итерационного процесса  , когда
, когда 


