
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Трехзначная нечеткая логика с учетом неопределенности и фактора времени и метасистемный подход в прогнозированииСодержание книги
Поиск на нашем сайте
Подшивалов Г.К., к.э.н. Российский университет дружбы народов Трехзначная нечеткая логика с учетом неопределенности и фактора времени и метасистемный подход в прогнозировании Часть 3. Трехзначная нечеткая фрактальная логика - Из-за такой малости! Из-за бабочки! - закричал Экельс. Она упала на пол - изящное маленькое создание, способное нарушить равновесие, повалились маленькие костяшки домино... большие костяшки... огромные костяшки, соединенные цепью неисчислимых лет, составляющих Время. Р. Бредбери. И грянул гром
В настоящей статье продолжено рассмотрение[1] проблем и методов решения задач стратегического планирования и прогнозирования на основе метасистемного подхода[2],[3],[4]. Продолжая тему, более детально рассмотрим комплекс проблем, связанных со стохастическими процессами в экономике, их хаотическим воздействием на экономические объекты, меняющим условия их хозяйственного функционирования, хозяйственную политику и стратегические цели. Хаотическое воздействие со стороны внешней среды свидетельствует о "революционности" возникшей ситуации, о переходе системы (политической, экономической) из устойчивой фазы эволюционной динамики в фазу катастрофы. Примерами подобной социальной хаотизированной динамики[5] могут служить так называемые "бархатные революции", которые произошли не так давно в ряде стран Европы, в том числе и на территории СНГ (Югославия, Украина, Грузия, Киргизия и др.) и привели к резкой дестабилизации, как политической, так и экономической. Опасность хаотизированной динамики состоит как в возможности ее "рецидивов" в рамках данной системы, так и в возможности ее распространения на системы, соседствующие с данной.
Постановка проблемы О цели разработки. Итак, перед нами стоит задача - разработка математического инструментария фрактальной логики. Для ее решения важно не только определить суть самого системного подхода при исследовании событий и процессов реальной действительности, но и выбрать наиболее эффективные методы и технологии построения такой логики. А для этого, находясь фактически на начальном, стартовом этапе разработки, необходимо определиться хотя бы в главном: · как разрабатывать эту "новую" логику; · в чем состоят сходство и различия этой логики с ранее разработанной нами трехзначной нечеткой логикой; · нельзя ли при разработке "новой" логики использовать мета-технологии, мета-инструментарий и логические операции нечеткой трехзначной логики.
О выдвижении новых требований. Поставив так вопросы, мы обратили внимание на то, что для осуществления разработки надо добавить к ранее выдвинутым требованиям ряд новых, которые связаны с более "жесткими" условиями функционирования самих систем (экономических, социальных, политических), так и с нестабильностью процессов, происходящих в их внешней среде. Теперь, при разработке этого нового математического инструментария логики, становится ясно, что недостаточно учитывать только различного вида неопределенности (хозяйственные, экономические, социальные, политические и др.), поскольку рассматриваемые системы перешли в качественно совершенно иные состояния функционирования. Фаза эволюционного развития для них уже завершена и начинается новая фаза - фаза "катастрофы", функционирование в рамках которой характеризуется более "жесткими" и нестабильными условиями,хаотической динамикой и многими катаклизмами, приводящими к полному разрушению систем и их распаду на отдельные "куски" - фракталы. Еще одна важная особенность этой "новой" логики связана с характером протекания нелинейных стохастических процессов, и прежде всего с их нестабильностью, многовариантностью развития и протекания во времени. О различии в типах логик. Если первая (уже разработанная нами нечеткая трехзначная логика с учетом фактора времени) – это логика для четких объектов с нечеткими свойствами, то вторая (нечеткая фрактальная логика, которую нам еще предстоит разработать) – это логика для нечетких объектов с нечеткими свойствами. Специфика нечеткости объектов фрактальной логики связана именно с тем, что "значениями" предметной переменной являются фракталы, а не отдельные действительные числа. В рамках рассмотренной нами ранее нечеткой трехзначной логики термам, с которыми связано задание значений лингвистической переменной, присваиваются не только те или иные значения истинности функции Однако для того, чтобы выполнить требования построения " предметных фракталов ", нам потребуется рассмотреть ряд операторов нового логического инструментария. О различиях в типах логистик и логистических системах. Фактически в любом виде деятельности: в экономике, политике, бизнесе, - необходимо принимать решения при развязке конкретных конфликтных ситуаций. Логистика произошла от греческого слова logistike - искусство рассуждать, обосновывать, выводить, доказывать, вычислять. История возникновения и развития этого термина уходит в далекое прошлое. Логистика – термин, употребляемый для обозначения систем логики, характеризующихся попыткой сведения логических рассуждений к формальным исчислениям. В экономике, бизнесе под логистикой понимается вид деятельности, связанный с передвижением (потоками) материалов, услуг, финансов и информации между экономическими субъектами, - например, обработка заказов, складирование продукции, ее комплектация, упаковка, транспортировка и т. д. Суть логистики применительно к этим видам деятельности связана именно с логическим анализом, выводом и принятием решения. Продвижение в реальной среде экономики и бизнеса материальных и финансовых потоков почти всегда связано с конфликтными ситуациями, несущими потери и риск для бизнеса и потребителей. Поэтому возникает потребность мониторинга ситуаций, анализа и своевременного устранения причин конфликта. В этом и состоит суть современного понимания в необходимости логического обоснования, формализованного рассуждения и вывода, т. е. современной расшифровки греческого слова logistike. О задачах автоматизации управления и принятия решений. Многие задачи управления сложными объектами без труда решаются человеком, но в силу различных обстоятельств требуют автоматизации. В таком случае опыт человека-специалиста может быть выражен в виде текста на естественном языке. Однако в большинстве случаев на практике приходится иметь дело с очень сложными системами, для которых управление становится весьма трудной задачей, если для него используется только количественная информация об объекте управления и его среде в виде баз данных. База данных – организованная совокупность данных, предназначенная для их эффективного хранения, накопления и обработки с помощью персональных компьютеров. В том случае, когда этих данных (об объекте управления и его среде) недостаточно для эффективного управления или когда их накопление и обработка становятся громоздкими, для управления применяют семантическую, т. е. смысловую, качественную информацию, на основе которой.формируется семантическая модель объекта. Под логико-лингвистической моделью управления понимается такая модель управления сложным объектом, в которой используется семантическая информация. Языком этого исчисления выбирается язык, называемый языком представления знаний. В качестве аксиом исчисления служат: - описания объекта управления, - описания его внешней среды, - описания начальных состояний. В качестве правил вывода служат правила перехода объекта из одного состояния в другое. В качестве теорем рассматриваются промежуточные и конечные состояния. Очень часто формальное представление информации об объекте включает в себя и данные, и знания. В этом случае б аза данных и знаний – это организованная совокупность данных и знаний об объекте управления, т. е. в такой модели используются и количественные данные, и семантическая информация. Общими принципами построения подобных "умных", или интеллектуальных, человеко-машинных систем являются следующие. 1. База данных и знаний должна содержать модель предметной области объекта и его среды. 2. Различные системы могут отличаться средствами представления данных. Например, часть б азы знаний может носить фундаментальный, стратегический характер, относясь к предметной области объекта. Эти знания могут достаточно медленно изменяться и пополняться. Другая же часть этих знаний носит оперативный характер и может претерпевать изменения более интенсивно. 3. Взаимодействие пользователя с этой системой осуществляется посредством "оболочки", представляющей пользовательский интерфейс: - для разработчиков и программистов, - для инженеров по знаниям. 4. Существенные отличия любой семиотической, т. е. знаковой или логико-лингвистической модели системы от традиционных систем управления определяются пятью моментами. Назовем их. · Наличие Модели Знаний. · Отделенность Модели Знаний от механизма Порождения Решений, что существенно упрощает описания состояний и функционирования. · Наличие Интерпретатора. · Наличие механизма Порождения Решений: на основе анализа состояния (ситуации), в которой находятся объект управления и среда, этот механизм должен позволять выбор некоторых решений. · Использование Машины Логического Вывода, или Интерпретатора, для ответа на поставленные пользователем вопросы.
. Для того, чтобы лучше понять современное толкование и инструментарий экономической логистики, заглянем в такую отрасль науки, как математика и математическая логика. Становление и развитие математической логики в конце 19-го и начале 20-го столетий было связано с необходимостью строгого, т. е. формального обоснования математики, теории множеств и ряда других точных наук. Появились совершенно новые инструменты для решения этих проблем: теория доказательств, теория формально-аксиоматических систем и исчислений. Специфической особенностью "умных" систем нового поколения является то, что их структура, методы и функции существенно отличаются от более "старых" автоматизированных человеко-машинных систем обработки информации и принятия решений. Так, если в более старых системах информация в основном была представлена в виде наборов данных, баз данных, а обработка этих данных осуществлялась на основе алгоритмов, не требующих применения дедуктивных методов, то в новых, "умных" сиcтемах качественно изменяются и структура информации, и методы ее обработки. Стало необходимым представлять информацию не только в виде баз данных, но и в виде баз знаний. Для формирования, накопления и обработки последних необходимо использовать логистические формализованные (дедуктивные) системы, которые позволяют представлять знания об исследуемом объекте в виде логических структур, состоящих из связок, констант, переменных, термов и предикатов, правил вывода. Поэтому стало необходимым включать в программное обеспечение таких систем программы, обеспечивающие логически обоснованный вывод для поисковых требований, представленных в форме отношений и предикатов, - сценариев отображающих реальные процессы. Формирование баз знаний, п оисковых запросов и их логическая обработка осуществляются специалистами по логистике. Для автоматизации обработки в таких системах, как правило, применяются различные специализированные языки логического программирования. Весьма важным при разработке таких прикладных автоматизированных бизнес-систем принятия тактических и стратегических решений, логистических и экспертных систем является выбор для них такой Логической Машины Вывода, которая была бы адекватна требованиям решаемых задач. Учитывая, что принятие многих стратегических решений в менеджменте сопряжено с фактором времени, с неопределенностью и риском в будущем, с форсмажорными обстоятельствами, к инструментарию таких «дедуктивных логических машин» - исчислений – предъявляются новые требования: возможность проводить «нестрогие» доказательства и выводы, оценивать их степень достоверности, учитывать фактор времени и неопределенность, учитывать переход динамики бизнес-систем из фазы эволюционного развития в фазу "катастрофы", когда динамика системы внезапно хаотизируется, а последняя теряет устойчивость. К сожалению, при разработке прикладных логистических систем использовались, большей частью, логические исчисления, не обеспечивающие этих требований, либо же вообще не ставился вопрос об их логическом обосновании и выводе. О различиях в функционировании. Обратим теперь внимание на два наиболее важных различия в функционировании логистических и фрактально-логистических систем. Первое из них связано с формированием баз знаний, а второе – с выполнением логических операций. При формированиии баз знаний в традиционных прикладных логистических системах с четкой двоичной логикой всем фактам-аксиомам присваивается максимальное значение истинности, равное единице. Для нечетких логистических систем это требование может быть "ослаблено" и в модель базы знаний могут быть включены квази-факты, которым присваиваются "огрубленные" значения истинности, например, "0.8" или "0.9", включаемые в достаточно близкую окрестность значения "1". Это позволяет в таких системах проводить так называемые нестрогие доказательства при осуществлении операций логического вывода. О базах знаний фрактальных логистических систем. При формированиии баз знаний во фрактальных логистических системах такого "огрубления" уже недостаточно. К ним предъявляются новые требования, связанные с необходимостью фиксации значений истинности аксиом-фактов во времени, а также их актуализация на заданный интервал времени. Неоднозначность и неустойчивость характера протекания нелинейных динамических процессов, многовариантность их развития во времени, вынуждает искать ответы на следующие вопросы: · как принимать решения в фазе катастрофы? · на какой основе должны строиться эти новые правила и операции логического вывода? · какой инструментарий использовать для фрактальной логики и логистики при разработке прикладных систем?
Общее правило, которого надо придерживаться при развитии катастроф, связанных со средой обитания, жизнью и деятельностью людей, звучит примерно так: помни, что истина не вечна! Это является следствием того, что в фазе катастрофы, разрушения и гибели социальной системы, в сознании людей, общества происходит такие потрясения, которые затрагивают их глубинные, ценностные и культурные основы. Можно привести примеры таких потрясений как из истории, так и из современной действительности, когда нарушались основные заповеди в обществе, в религиях. Нарушения, например, таких известных и основных заповедей-аксиом, как "не убий", "не грабь", во времена смут, войн или революций приводит к тому, что их изъятие из "доказательной базы" способствует установлению "новых правил" революционной целесообразности - игры, в ходе которой устанавливаются и "новые основы логического вывода". Как следствие этого, то что было под запретом, становится дозволенным. Если это связано с бизнесом, то он – криминален, если политики, то она - грязная и т. д. Мы привели эти примеры для того, чтобы заострить внимание на специфике процессов и систем с нелинейной динамикой, со сложностью, а порой и недостовернотью информации, используемой при развитии катастроф для принятия решений. "Лекарством" от этого должны служить не только процедура " актуализации " баз данных и знаний, но и их фильтрация от "фрактального мусора" – аксиом-"знаний" с низким уровнем значений нечеткой "правды" после применения к ним фрактальных кванторов. Суть такой фильтрации состоит в исключении их из доказательной базы логистических систем. В ходе выполнения этих операций формируются новые значения как для предметных переменных, так и для состояний истинности (термов). О нечеткой трехзначной логике - базе для построения фрактальной логики. Фактически добавление двух фрактальных кванторов необходимо учитывать после выполнении каждой из логических операций, определенных ранее в рамках разработанной нами нечеткой трехзначной логики. Поэтому настоящая разработка, по сути, является развитием математического инструментария нечеткой трехзначной логики. Операции этой логики были определены нами в двух первых частях разработки[6]. В этой третьей части разработки нам лишь требуется после выполнения каждой такой операции добавить к ней цепочку фрактальных кванторов "фазификации-дефазификации ". Переходим к более подробному рассмотрению кванторов и операций с ними.
Операция импликации В результате выполнения операции
После чего и предметная переменная
Все остальные логические операции преобразуются по этой же схеме. Считаем, что примеров приведено достаточно, чтобы понять общую схему выполнения преобразований фрактальных логических операций и перейти к рассмотрению проблем, связанных с разработкой модели дискретного итерационного процесса.
Фракталы как предвестники катастроф и фрактальная логика Термины "фрактал" и "фрактальная геометрия" появились в конце 1970-х гг. и с середины 1980-х гг. прочно вошли в обиход математиков и программистов. Слово " фрактал" образовано от латинского fractus и в переводе означает " состоящий из фрагментов". Оно было предложено Бенуа Мандельбротом в 1975 году для обозначения нерегулярных, но самоподобных структур, изучением которых он занимался[9], [10]. Исследуя биржевую статистику и аналитику по ценам на хлопок, непредсказуемые взлеты и обвалы этих цен, Мандельброт обнаружил, что произвольные, на первый взгляд, колебания в ценах могут следовать скрытому математическому порядку во времени, который не соответствует стандартным кривым, обычно изображаемым в традиционной статистике. Результаты анализа биржевых колебаний цены хлопка в течение дня, проведенного Бенуа Мандельбротом по новому методу, оказались ошеломляющими не только для его самого, но и для биржевых аналитиков. Суть метода, примененного Мандельбротом, сводилась к следующему. Имелись надежные данные по ценам на хлопок более, чем за сто лет. Колебания цены в течение дня были непредсказуемы, но компьютерный анализ показал тенденцию изменения цены. Мандельброт сопоставил график колебания цены в течение одного дня с графиком колебаний цен за более длительный период времени. Наложив графики друг на друга, он обнаружил симметрию длительных колебаний цены и колебаний кратковременных. Это сбило с толку и удивило экономистов. Даже для самого Бенуа Мандельброта полный смысл этого открытия был сначала до конца не ясен. Только позже он понял, что начал разрабатывать рекурсивный фрактальный метод в экономике. Наблюдения над процессами объективной реальности, в которых проявляются фрактальные свойства, убеждают нас в том, что фракталы, в случаях, когда их появление фиксируется, – это " буревестники", которые всегда появляются перед бурей. Они – SOS-сигналы систем,переходящих в фазу катастрофы [11]. Важно и то, что разрушение, фрактализация систем, т. е. их распадение на части – фракталы – происходит при появлении в них особого рода симметрии. Она проявляется в геометрическом масштабе, в формах динамики во времени, в алгоритмических «повторах». Основной т ип симметрии, передаваемой фракталам, - это – самоподобие, самоаффинность, т. е. свойства того «портрета» системы, который может «запомниться» перед ее разрушением. Безусловно, общее количество "портретов", этих "предсмертных масок" системы и их состояний, ведущих к ее хаотизации или полному разрушению, практически может быть неограниченно. Важно обратить внимание на то, что общее количество этих "портретов" отражает переход из состояния, когда система рассматривается как единое целое, в качественно иные состояния – состояния "ансамбля кусков". Для этого "ансамбля кусков" характерно, прежде всего, такое его свойство, как нечеткость и неопределенность заданности. Поэтому данный тип "ансамбля" можно классифицировать еще и как нечеткую, хаотизированную, нелинейную, динамическую систему с неустойчивыми параметрами. Как вы думаете, какой тип логики наиболее подходит для формализации этих ансамблей систем, - например, при прогнозировании динамики и обосновании прогнозных сценариев? На наш взгляд, ответ очевиден. Это должна быть нечеткая фрактальная трехзначная логика, т. е. логика для нечетких объектов с нечеткими свойствами, учитывающая неопределенность и фактор времени в процессах развития катастроф. И, безусловно, разработкатакой фрактальной логики должна осуществляться на основеметасистемного подхода.
Общие требования к разработе метасистемного инструментария Перед началом процесса моделирования приведем, в качестве шутки, один из известных философских казусов-вопросов, который волновал философов в конце 19-го и начале 20-го столетий: "Что первично: яйцо или курица?" На наш взгляд, с позиций математика-разработчика, вопрос не вполне корректен. Ведь даже известный сказочный герой папа Карло для изготовления Буратино имел свой традиционный инструмент (топор). Разработка "хорошего яйца" невозможна без "хорошей курицы". Поэтому, упомянутый вопрос "о первичности", на наш взгляд, отпадает сам собой, а вот требования, предъявляемые к метасистемному инструментарию – "курице" – играют очень важную роль. Любому математику, ставящему перед собой цель разработки качественно новой модели задачи или математического аппарата, например, фрактальной логики, или,образно говоря, задачу "снести фрактальное яйцо", прежде всего потребуется "курица" – сформулированный и обоснованный метасистемный инструментарий. Важно, чтобы мета-аксиомы и мета-правила вывода этого инструментария были обоснованы, полны и непротиворечивы, а вопрос о том, будет ли достаточным использование лишь традиционных математических понятий или же потребуется ввести в разработку новые понятия, операторы и кванторы, является открытым, так как в этом процессе необходимо выделить наиболее важные, существенные свойства иотбросить все лишнее. Особенность разработок, осуществляемых на базе метасистемного подхода, состоит в том, что в них создание "курицы" – метасистемы - предшествует созданию "яйца" – системы (или процесса). В нашем случае в роли одного из таких "яиц" выступает уравнение дискретного итерируемого процесса. Но весь фокус разработки как раз и состоит в том, что при создании "курицы" (метасистемы) должны учитываться совершенно новые требования внутренней непротиворечивости и конструктивной замкнутости к разрабатываемому "яйцу", так как без этого "яйцо" не будет правильно функционировать или "расколется". Эти новые требования должны включаться в метасистему как необходимые мета-аксиомы и мета-правила вывода. Формализация последних должна проявляться в разрабатываемых моделях систем (или процессов) в неких формах инвариантности - "законах" сохранения формы взаимосвязи функциональных переменных относительно всех существенных блоков факторов, включаемых в модель.
Фрактальная парадигма хаоса Вкратце охарактеризуем новую и уже весьма распространенную в современной науке парадигму - парадигму хаоса. В нашей разработке мы также будем ее использовать. Конец прошлого столетия ознаменовался новыми идеями, теориями и фундаментальными открытиями в науке, в числу которых принадлежат и открытия, связанные с теорией хаоса, фрактальной геометрией, синергетикой, теорией нелинейных динамических систем, теорией диссипативных структур и процессов. В различных отраслях научного знания появилось множество публикаций, связанных с применением этих теорий - и прежде всего теорий фракталов и хаоса - в целом ряде прикладных разработок (например, использованием теорий хаоса и фракталов в биржевой аналитике, в биотехнологиях, радиосвязи, компьютерных информационных технологиях и др. Ученым стало ясно, что практически все наблюдаемые и исследуемые объекты природы имеют фрактальный характер. Даже хаос как объект исследования современной физики стал рассматриваться не как "мера беспорядка", а как нечто, имеющее более высокую степень (фрактальной) организованности материи. Фрактальный характер объектов проявляется в их дробной размерности. Например, такие объекты могут иметь размерность 0,7 или 1,3, или 2,6. Поэтому в привычных для нашего восприятия одномерных, двумерных и трехмерных пространствах такие объекты не могут наблюдаться во всей полноте и «тают» в нашем представлении, словно “ежик в тумане”. Нечеткость фрактальных объектов не только проявляется в их свойствах. Она заложена в самой «природе» объектов. Фракталы по своей природе – это нечеткие объекты с нечеткими свойствами, нечеткой геометрией и нечеткими алгоритмами, проявляющимися в особых формах симметрии – самоподобии, самоафинности. Им свойственны также формы симметрии и более высоких порядков, выражающиеся не только в виде линейных, но и в виде степенных и иных зависимостей. Если применять традиционные экстраполятивные математические методы и приемы при прогнозировании, то, как правило, поведение нелинейных систем непредсказуемо, даже для систем с простой структурой. Все попытки объяснить это поведение привычными методами линейной математики обречены на неудачу. Так, например, непредсказуемо поведение участников каких-либо экономических, политических или социальных схем. Их участники, вступая в "игру" или "революции", образуют системы с неустойчивыми параметрами, поведение которых невозможно предсказать. По-видимому, существуют необъяснимые "законы хаоса" для этих систем, следуя которым, с неотступной периодичностью наступают фазы кризиса, депрессии, оживления и подъема для этих систем в целом. Другими словами, в этой хаотической непредсказуемости имеется некий строгий порядок. Рассмотрим пример использования возможностей нового научного подхода и современных представлений "об организационной сложности" объектов к анализу социально-экономических систем. Одним из таких примеров "сложной" системы является любое современное государство. В рамках такой системы можно выделить столь злободневную для нас проблему "управления кризисами". Под кризисом понимается такое состояние системы, когда она находится в непосредственной окрестности или прямо в точке бифуркации, т. е. когда состояние системы способно качественным образом измениться. Хаос, в котором пребывает находящаяся в кризисном состоянии система, внешне похож на обычную неразбериху. Состояние системы видимым образом обусловлено совокупным действием множества причин: характер хаотической динамики сопровождается непредсказуемыми, асинхронными и разноамплитудными всплесками, отсутствием какого-либо порядка и т. п. Система пребывает в крайне неустойчивом, кризисном положении, как застывший над пропастью канатоходец, она потенциально готова совершить бифуркацию. Даже легкий порыв ветра способен сбросить канатоходца в пропасть, это - стандартная ситуация, когда "верхи не могут, а низы не хотят". Удивительная особенность хаоса в том, что такие системы, как бы велики они не были, очень легко управляемы. Канатоходцу для этого достаточно пошевелить пальцем, в крайнем случае, взмахнуть рукой. Нужно только в нужный момент помочь системе, или как мы говорим, канатоходцу - удержаться. Для этого достаточно выполнить незаметное, легкое корректирующее движение.
Системы итерируемых функций В области точных наук век линейной алгебры, линейных процессов закончился, и теперь в физике, математике, химии, экономике, социалогии и политологии, а также на стыках комплекса дисциплин есть множество нелинейных задач. Среди них - и нелинейная оптика, и колебательные реакции, и нелинейная оптимизация, и нелинейная фрактальная теория организаций, и нелинейная фрактальная теория переходных экономических процессов. Но одна из самых перспективных возможностей применения нелинейных систем в компьютерных информационных технологиях фрактальное сжатие изображений. При этом под термином "изображение" следует понимать не только графические изображения, можно рассматривать “изображения”-модели в более широком смысле, - как сжатие моделей. Ведь не случайно, согласно одному из определений данного термина, его суть сводится к утверждению, что “модель” - это изображение, образ системы-оригинала. Разработка теоретических основ данного перспективного направления связана с известным математиком Девэйни (Devaney), который предположил, что " функцию сжатия изображений" можно определить как хаотическую, если она сильно зависит от начальных условий, а точки диаграммы (графика) плотно сближаются как бы в одну цельную структуру. Хотя это и непредсказуемо, но все же содержит регулярность (рекурсию), так как на таком графике зависимости от параметра, называемого бифуркационной диаграммой, можно видеть топологию границ и линии структуры, пересекающие весь этот, казалось бы, хаос, по определенным траекториям. Своей потрясающей воображение красотой фракталы обязаны именно этой, если можно так выразиться, "упорядоченности", структуре, возникающей по необъяснимым законам хаоса. Это еще раз подчеркивает мысль, что хаос фрактален и раскрывает смысл так называемой фрактальной парадигмы хаоса. В 1981 году вышла книга Джона Хатчинсона (John Hutchinson) "Фракталы и самоподобие", и в математике стало одной теорией больше. Появилась теория итерируемых функций (iterated function theory). В 1985 г. Майкл Барнсли (Michael Barnsley), ведущий исследователь фирмы Georgia Tech, опубликовал свою работу, в которой ввёл в математику понятие " системы итерируемых функций" (IFS), доказав, что с её помощью можно представить любое изображение. В 1990 г. Барнсли получил патент на технологию IFS, а в 1991г. запатентовал и усовершенствованную версию - PIFS. Хотя Барнсли доказал теоретически возможность компрессии изображений в сотни и тысячи раз и даже опубликовал несколько искусственно созданных картин со сжатием 10000:1, он не мог автоматизировать процесс компрессии, и всю работу приходилось делать вручную студентам университета, где Барнсли преподавал. Но вот в 1992 году один из его студентов, которому, судя по всему, это надоело, - Арно Жакуин (Arnaud Jacquin) - предложил первый практический метод автоматизированной компрессии изображений. Алгоритм Жакуина лёг в основу коммерческого компрессора-декомпрессора компании Iterated Systems Incorporated и используется до сих пор. Если говорить о фрактальных методах сжатия изображений, то нельзя не отметить, что эта тема до сих пор исследована далеко не полностью, несмотря на всю её актуальность. Фрактальные архиваторы графических файлов нашли широкое применение у пользователей и специалистов. Однако решение новых проблем модельного сжатия позволит существенно повысить производительность процессоров и, следовательно, увеличить скорость обработки информации. Эти компьютерные технологии рассчитаны наболее профессиональных пользователей и специалистов, они так и остаются все еще неразработанными. Одна из проблем – повышение скорости выполнения итераций и сохранение хорошего качества компрессии. До сих пор не решена проблема нахождения оптимального метода сжатия с максимальной точностью при больших скоростях компрессии и большом числе итераций. Например, для вычисления изображения формата 256x256 пикселов, используя метод Жакуина, нужно просчитать около 31-го миллиарда итераций. Еще одно важное свойство фракталов – это многозначность возникновения переходных процессов вблизи точек бифуркаций. Фазовое пространство процессов, протекающих в нелинейных динамических системах, подразделяется на области, как правило, с несколькими аттракт
|
||||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 291; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.15.124 (0.025 с.) |

 , но и значения
, но и значения 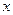 -объектов. При этом последние фиксируются только на предметной оси - оси действительных чисел
-объектов. При этом последние фиксируются только на предметной оси - оси действительных чисел  . Таким образом, любое из этих значений всегда является действительным числом, которое "четко" фиксируется как точка на данной оси. В рамках нечеткой логики каждому такому "четкому", "точечному" значению переменной
. Таким образом, любое из этих значений всегда является действительным числом, которое "четко" фиксируется как точка на данной оси. В рамках нечеткой логики каждому такому "четкому", "точечному" значению переменной  . В рамках такой нечеткой трехзначной логики, предложенной нами ранее, мы уже рассматривали операции над нечеткими множествами и отношениями.
. В рамках такой нечеткой трехзначной логики, предложенной нами ранее, мы уже рассматривали операции над нечеткими множествами и отношениями. на начальном этапе будут вычислены компоненты функции принадлежности по формулам:
на начальном этапе будут вычислены компоненты функции принадлежности по формулам: ;
; ;
;
 будут приведены к комплексной форме:
будут приведены к комплексной форме:  и
и  . Далее, как мы уже отметили, следует выполнение кванторов фрактальной фазификации и дефазификации.
. Далее, как мы уже отметили, следует выполнение кванторов фрактальной фазификации и дефазификации.


