
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Хаос, стохастика, аттракторы и бифуркацииСодержание книги
Поиск на нашем сайте В рамках данной статьи мы будем использовать при разработке фрактальной логики аппарат стохастических систем и стохастическую динамику на комплексной плоскости. Поэтому с аттрактором ( на комплексной плоскости) мы будем связывать точку или предельный цикл, на которых сходится процесс итераций
Фрактальная парадигма хаоса Вкратце охарактеризуем новую и уже весьма распространенную в современной науке парадигму - парадигму хаоса. В нашей разработке мы также будем ее использовать. Конец прошлого столетия ознаменовался новыми идеями, теориями и фундаментальными открытиями в науке, в числу которых принадлежат и открытия, связанные с теорией хаоса, фрактальной геометрией, синергетикой, теорией нелинейных динамических систем, теорией диссипативных структур и процессов. В различных отраслях научного знания появилось множество публикаций, связанных с применением этих теорий - и прежде всего теорий фракталов и хаоса - в целом ряде прикладных разработок (например, использованием теорий хаоса и фракталов в биржевой аналитике, в биотехнологиях, радиосвязи, компьютерных информационных технологиях и др. Ученым стало ясно, что практически все наблюдаемые и исследуемые объекты природы имеют фрактальный характер. Даже хаос как объект исследования современной физики стал рассматриваться не как "мера беспорядка", а как нечто, имеющее более высокую степень (фрактальной) организованности материи. Фрактальный характер объектов проявляется в их дробной размерности. Например, такие объекты могут иметь размерность 0,7 или 1,3, или 2,6. Поэтому в привычных для нашего восприятия одномерных, двумерных и трехмерных пространствах такие объекты не могут наблюдаться во всей полноте и «тают» в нашем представлении, словно “ежик в тумане”. Нечеткость фрактальных объектов не только проявляется в их свойствах. Она заложена в самой «природе» объектов. Фракталы по своей природе – это нечеткие объекты с нечеткими свойствами, нечеткой геометрией и нечеткими алгоритмами, проявляющимися в особых формах симметрии – самоподобии, самоафинности. Им свойственны также формы симметрии и более высоких порядков, выражающиеся не только в виде линейных, но и в виде степенных и иных зависимостей. Если применять традиционные экстраполятивные математические методы и приемы при прогнозировании, то, как правило, поведение нелинейных систем непредсказуемо, даже для систем с простой структурой. Все попытки объяснить это поведение привычными методами линейной математики обречены на неудачу. Так, например, непредсказуемо поведение участников каких-либо экономических, политических или социальных схем. Их участники, вступая в "игру" или "революции", образуют системы с неустойчивыми параметрами, поведение которых невозможно предсказать. По-видимому, существуют необъяснимые "законы хаоса" для этих систем, следуя которым, с неотступной периодичностью наступают фазы кризиса, депрессии, оживления и подъема для этих систем в целом. Другими словами, в этой хаотической непредсказуемости имеется некий строгий порядок. Рассмотрим пример использования возможностей нового научного подхода и современных представлений "об организационной сложности" объектов к анализу социально-экономических систем. Одним из таких примеров "сложной" системы является любое современное государство. В рамках такой системы можно выделить столь злободневную для нас проблему "управления кризисами". Под кризисом понимается такое состояние системы, когда она находится в непосредственной окрестности или прямо в точке бифуркации, т. е. когда состояние системы способно качественным образом измениться. Хаос, в котором пребывает находящаяся в кризисном состоянии система, внешне похож на обычную неразбериху. Состояние системы видимым образом обусловлено совокупным действием множества причин: характер хаотической динамики сопровождается непредсказуемыми, асинхронными и разноамплитудными всплесками, отсутствием какого-либо порядка и т. п. Система пребывает в крайне неустойчивом, кризисном положении, как застывший над пропастью канатоходец, она потенциально готова совершить бифуркацию. Даже легкий порыв ветра способен сбросить канатоходца в пропасть, это - стандартная ситуация, когда "верхи не могут, а низы не хотят". Удивительная особенность хаоса в том, что такие системы, как бы велики они не были, очень легко управляемы. Канатоходцу для этого достаточно пошевелить пальцем, в крайнем случае, взмахнуть рукой. Нужно только в нужный момент помочь системе, или как мы говорим, канатоходцу - удержаться. Для этого достаточно выполнить незаметное, легкое корректирующее движение.
|
||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 502; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

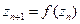 при
при 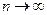 . В роли аттрактора может выступать притягивающая неподвижная точка или притягивающий цикл определенного периода. Иногда таких аттракторов может быть несколько, они также могут состоять из бесчисленного количества точек и представлять собой какое-нибудь другое множество. Если же в процессе итераций изображающая их точка уходит на бесконечность, то аттрактором такого процесса считается бесконечно удаленная точка. Термин " бифуркация " буквально означает " раздвоение " и употребляется как название любого скачкообразного изменения, происходящего при плавном изменении параметров в любой из динамических систем: экономической, социальной, системах термо- и газодинамики. Для формального описания состояний таких систем используется фазовое пространство переменных. Семейства траекторий системы в фазовом пространстве образуют ее фазовый портрет. Бифуркации проявляются в резком изменении фазового портрета.
. В роли аттрактора может выступать притягивающая неподвижная точка или притягивающий цикл определенного периода. Иногда таких аттракторов может быть несколько, они также могут состоять из бесчисленного количества точек и представлять собой какое-нибудь другое множество. Если же в процессе итераций изображающая их точка уходит на бесконечность, то аттрактором такого процесса считается бесконечно удаленная точка. Термин " бифуркация " буквально означает " раздвоение " и употребляется как название любого скачкообразного изменения, происходящего при плавном изменении параметров в любой из динамических систем: экономической, социальной, системах термо- и газодинамики. Для формального описания состояний таких систем используется фазовое пространство переменных. Семейства траекторий системы в фазовом пространстве образуют ее фазовый портрет. Бифуркации проявляются в резком изменении фазового портрета.


