
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операция дизъюнкции (объединения)Содержание книги
Поиск на нашем сайте
В результате выполнения операции
После чего и предметная переменная
Операция исключающей дизъюнкции (искючающего объединения) двух нечетких множеств В результате выполнения операции
После чего и предметная переменная Операция конъюнкции (пересечения) двух нечетких множеств В результате выполнения операции
После чего и предметная переменная Операция импликации В результате выполнения операции
После чего и предметная переменная
Все остальные логические операции преобразуются по этой же схеме. Считаем, что примеров приведено достаточно, чтобы понять общую схему выполнения преобразований фрактальных логических операций и перейти к рассмотрению проблем, связанных с разработкой модели дискретного итерационного процесса.
Фракталы как предвестники катастроф и фрактальная логика Термины "фрактал" и "фрактальная геометрия" появились в конце 1970-х гг. и с середины 1980-х гг. прочно вошли в обиход математиков и программистов. Слово " фрактал" образовано от латинского fractus и в переводе означает " состоящий из фрагментов". Оно было предложено Бенуа Мандельбротом в 1975 году для обозначения нерегулярных, но самоподобных структур, изучением которых он занимался[9], [10]. Исследуя биржевую статистику и аналитику по ценам на хлопок, непредсказуемые взлеты и обвалы этих цен, Мандельброт обнаружил, что произвольные, на первый взгляд, колебания в ценах могут следовать скрытому математическому порядку во времени, который не соответствует стандартным кривым, обычно изображаемым в традиционной статистике. Результаты анализа биржевых колебаний цены хлопка в течение дня, проведенного Бенуа Мандельбротом по новому методу, оказались ошеломляющими не только для его самого, но и для биржевых аналитиков. Суть метода, примененного Мандельбротом, сводилась к следующему. Имелись надежные данные по ценам на хлопок более, чем за сто лет. Колебания цены в течение дня были непредсказуемы, но компьютерный анализ показал тенденцию изменения цены. Мандельброт сопоставил график колебания цены в течение одного дня с графиком колебаний цен за более длительный период времени. Наложив графики друг на друга, он обнаружил симметрию длительных колебаний цены и колебаний кратковременных. Это сбило с толку и удивило экономистов. Даже для самого Бенуа Мандельброта полный смысл этого открытия был сначала до конца не ясен. Только позже он понял, что начал разрабатывать рекурсивный фрактальный метод в экономике. Наблюдения над процессами объективной реальности, в которых проявляются фрактальные свойства, убеждают нас в том, что фракталы, в случаях, когда их появление фиксируется, – это " буревестники", которые всегда появляются перед бурей. Они – SOS-сигналы систем,переходящих в фазу катастрофы [11]. Важно и то, что разрушение, фрактализация систем, т. е. их распадение на части – фракталы – происходит при появлении в них особого рода симметрии. Она проявляется в геометрическом масштабе, в формах динамики во времени, в алгоритмических «повторах». Основной т ип симметрии, передаваемой фракталам, - это – самоподобие, самоаффинность, т. е. свойства того «портрета» системы, который может «запомниться» перед ее разрушением. Безусловно, общее количество "портретов", этих "предсмертных масок" системы и их состояний, ведущих к ее хаотизации или полному разрушению, практически может быть неограниченно. Важно обратить внимание на то, что общее количество этих "портретов" отражает переход из состояния, когда система рассматривается как единое целое, в качественно иные состояния – состояния "ансамбля кусков". Для этого "ансамбля кусков" характерно, прежде всего, такое его свойство, как нечеткость и неопределенность заданности. Поэтому данный тип "ансамбля" можно классифицировать еще и как нечеткую, хаотизированную, нелинейную, динамическую систему с неустойчивыми параметрами. Как вы думаете, какой тип логики наиболее подходит для формализации этих ансамблей систем, - например, при прогнозировании динамики и обосновании прогнозных сценариев? На наш взгляд, ответ очевиден. Это должна быть нечеткая фрактальная трехзначная логика, т. е. логика для нечетких объектов с нечеткими свойствами, учитывающая неопределенность и фактор времени в процессах развития катастроф. И, безусловно, разработкатакой фрактальной логики должна осуществляться на основеметасистемного подхода.
Общие требования к разработе метасистемного инструментария Перед началом процесса моделирования приведем, в качестве шутки, один из известных философских казусов-вопросов, который волновал философов в конце 19-го и начале 20-го столетий: "Что первично: яйцо или курица?" На наш взгляд, с позиций математика-разработчика, вопрос не вполне корректен. Ведь даже известный сказочный герой папа Карло для изготовления Буратино имел свой традиционный инструмент (топор). Разработка "хорошего яйца" невозможна без "хорошей курицы". Поэтому, упомянутый вопрос "о первичности", на наш взгляд, отпадает сам собой, а вот требования, предъявляемые к метасистемному инструментарию – "курице" – играют очень важную роль. Любому математику, ставящему перед собой цель разработки качественно новой модели задачи или математического аппарата, например, фрактальной логики, или,образно говоря, задачу "снести фрактальное яйцо", прежде всего потребуется "курица" – сформулированный и обоснованный метасистемный инструментарий. Важно, чтобы мета-аксиомы и мета-правила вывода этого инструментария были обоснованы, полны и непротиворечивы, а вопрос о том, будет ли достаточным использование лишь традиционных математических понятий или же потребуется ввести в разработку новые понятия, операторы и кванторы, является открытым, так как в этом процессе необходимо выделить наиболее важные, существенные свойства иотбросить все лишнее. Особенность разработок, осуществляемых на базе метасистемного подхода, состоит в том, что в них создание "курицы" – метасистемы - предшествует созданию "яйца" – системы (или процесса). В нашем случае в роли одного из таких "яиц" выступает уравнение дискретного итерируемого процесса. Но весь фокус разработки как раз и состоит в том, что при создании "курицы" (метасистемы) должны учитываться совершенно новые требования внутренней непротиворечивости и конструктивной замкнутости к разрабатываемому "яйцу", так как без этого "яйцо" не будет правильно функционировать или "расколется". Эти новые требования должны включаться в метасистему как необходимые мета-аксиомы и мета-правила вывода. Формализация последних должна проявляться в разрабатываемых моделях систем (или процессов) в неких формах инвариантности - "законах" сохранения формы взаимосвязи функциональных переменных относительно всех существенных блоков факторов, включаемых в модель.
|
||||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 174; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.34.93 (0.01 с.) |

 на начальном этапе будут вычислены компоненты функции принадлежности по формулам:
на начальном этапе будут вычислены компоненты функции принадлежности по формулам: ;
; ;
; .
.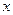 для всех элементов множеств, и соответствующая ей функция принадлежности
для всех элементов множеств, и соответствующая ей функция принадлежности  будут приведены к комплексной форме:
будут приведены к комплексной форме:  и
и  . Далее, как мы уже отметили, следует выполнение кванторов фрактальной фазификации и дефазификации.
. Далее, как мы уже отметили, следует выполнение кванторов фрактальной фазификации и дефазификации. на начальном этапе будут вычислены компоненты функции принадлежности по формулам:
на начальном этапе будут вычислены компоненты функции принадлежности по формулам: ;
; ;
; .
. будут приведены к комплексной форме:
будут приведены к комплексной форме:  на начальном этапе будут вычислены компоненты функции принадлежности по формулам:
на начальном этапе будут вычислены компоненты функции принадлежности по формулам: ;
;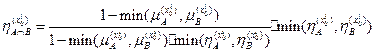 ;
; .
. на начальном этапе будут вычислены компоненты функции принадлежности по формулам:
на начальном этапе будут вычислены компоненты функции принадлежности по формулам: ;
; ;
;
 будут приведены к комплексной форме:
будут приведены к комплексной форме: 


