
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Число – важнейший математический объектСодержание книги
Поиск на нашем сайте
Основными объектами математики всегда являлись числа. Число – важнейшее математическое понятие. Возникнув в простейшем виде еще в первобытном обществе, понятие "числа " изменялось на протяжении веков, постепенно обогащаясь содержанием по мере расширения сферы человеческой деятельности, связанного с ним расширения круга вопросов, требовавшего количественного описания и исследования. На первых ступенях развития, понятие "числа" определялось потребностями счета, измерения и установления порядка, возникавшими в непосредственной практической деятельности человека. Затем оно (число) становится основным понятием математики, определяется потребностями науки. Понятие натурального числа было вызвано потребностями счета. Важным шагом в понятии натурального числа явилось осознание бесконечности натурального ряда, т. е. в потенциальной возможности его безграничного продолжения. Отчетливое представление о бесконечности натурального ряда сопряжено с трудами таких выдающихся античных философов и ученых, как Евклид - автор первого из дошедших до нас теоретических трактатов по математике, и Архимед – математик, механик, один из создателей механики как науки. Вопрос об обосновании понятия натурального числа долгое время в науке не ставился. Лишь во второй половине 19-го столетия под влиянием развития формально-аксиоматического метода в математике, с одной стороны, и пересмотра основ математического анализа, – с другой, назрела необходимость обоснования понятия количественного натурального числа. Так, определение "числа", данное Георгом Кантором, было отправным пунктом для обобщения понятия количественной характеристики бесконечных множеств. Исторически расширением понятия числа является дополнение натуральных чисел дробными числами. Введение в употребление дробных чисел связано с потребностью производить измерения. Дальнейшее расширение понятия числа обусловлено уже не непосредственными потребностями счета и измерения, оно стало следствием развития математики. Так, введение отрицательных чисел было вызвано развитием алгебры как науки, дающей общие способы решения арифметических задач, в числе которых важное место занимают методы решения линейных уравнений. Числа целые и дробные (положительные и отрицательные) получили общее название рациональных чисел. Но совокупность рациональных чисел оказалась недостаточной для решения задач нового типа – задач, связанных со взятием пределов, интегралов, решением дифференциальных уравнений, в которых использовались непрерывно изменяющиеся переменные величины. Потребовалось ввести новое расширение понятия числа – перейти от множества рациональных чисел к множеству действительных (вещественных) чисел. Этот переход состоит в присоединении к рациональным числам так называемых иррациональных чисел. Одним из следующих этапов расширения понятия числа явилось введение комплексныхчисел. Впервые идея комплексного числа появилась еще в 16-ом веке. Она была связана с решением алгебраических уравнений 3-й степени, Автор метода - Джероламо Кардано (1501 – 1576 г.), итальянский математик, философ и врач. Но особое значение в математике комплексныые числа приобрели в 19 – 20 столетиях. Это было связано с решением новых задач в аэро- и гидродинамике, термодинамике, космонавтике, в становлении и развитием новых теорий - теории нелинейных динамических систем, диссипативных процессов, синергетике, теории фракталов и хаоса.
Другой математик, наш современник, Бенуа Мандельбротт – основатель фрактальной геометрии, применил зависимость С появлением нового направления в вычислительной математике - так называемых мягких вычислений [19] (термин введен Лотфи А. Заде) появилась необходимость рассмотрения " мягких чисел". И хотя этот тип этих чисел еще не рассмотрен в математике и ему не дано научного определения, мы можем предположить, что это – "не за горами".
Но вот что важно для нас: какими числами осуществлять отображение свойств нечетких фрактальных объектов к действительным числам, с которыми мы связываем на практике все свои измерения и наблюдения? Хватит ли существенных свойств этих " числовых объектов" при формализации фрактальных систем, исчислений и теорий, и в частности, при разработке формальной логики? Или же нам потребуется ввести в рассмотрение новый вид чисел? Ответы на все эти вопросы должны быть получены на этапе конструирования метасистемного инструментария, т. е. уже в ходе данного исследования. Интуиция подсказывает, что не так все просто, поскольку фракталы как объекты по своим свойствам весьма специфичны. Но вначале сделаем небольшое отступление, чтобы сделать более понятной возникшую проблему. На наш взгляд, представляет определенный интерес проведение аналогии между принятой классификацией чисел и принятой классификацией фракталов. Фракталы классифицируются на: геометрические, алгебраические и стохастические. Первые (геометрические) строят на основе геометрических построений. Это - известные фракталы, например, пыль Кантора, снежинка Коха, салфетка и ковер Серпинского, губка Менгера, двойной дракон Хартера-Хейтуэля и др. Вторые (алгебраические), это – наиболее распространенный тип фракталов, к нему, в частности относится и фрактал Мандельброта. Этот тип, имеющий название "алгебраические", определяется на основе алгебраических полиномов Из рассмотрения этих аналогий можно сделать вывод о том, чтоспособ получения как чисел, так и фракталов отражается на их классификации. Из этого также следует, что от выбора вида уравнения дискретного итерационного процесса зависят свойства фракталов, которые порождаются последовательностями чисел. Динамика этих чисел может демонстрировать совершенно новые свойства - свойства фрактальной рекурсивной зависимости. Проявление специфики этих свойств – следствие выбора модели итерируемого процесса. В связи с этим гипотеза о рассмотрении "новых чисел" приобретает смысл в рамках даже этой разработки. Идея "новых чисел", обладающих особыми "гибридными" свойствами, этаких новых математических "кентавров", не лишена смысла. Давайте попытаемся, хотя бы на основе качественного анализа, понять на чем мы "буксуем". Прежде всего, отметим, что, при исследовании различных нелинейных систем и процессов с нелинейной динамикой, обращает на себя внимание то, что, все связанное с их развитием, носит ярко выраженный диалектический характер. В динамику, как правило, "включаются" сразу несколько факторов, имеющих противоположные, "конкурирующие" тенденции, носящие характер диалектического "единства и борьбы противоположностей". И если в таких нелинейных динамических системах (или процессах) производятся какие-либо "числовые" измерения и обработка данных, то в их "характере" проявляются совершенно "новые" свойства чисел. Поэтому нам надо ввести в рассмотрение соответствующий тип итеративных процессов, порождающих "новые числа", т. е. числа, в динамике которых проявлялись бы как рекурсивные свойства совокупности отдельных факторов, так и "диалектика" их взаимодействия. Заметим, что в такой постановке решение дилеммы "рекурсия-диалектика" при моделировании дискретного итерационного процесса становится много сложнее, чем форма рекурсии при порождении чисел Фибоначчи
Нам представляется необходимым включить данную диллему в перечень наиболее важных существенных свойств при рассмотрении процессов нелинейной динамики. Этот перечень состоит из следующих пунктов:
· "память о прошлом" или "статистичность"; · "забывание прошлого", которое связано с локальной неустойчивостью и хаосом; · алгоритмичность, проявляющаяся в алгоритмических "повторах"; · "нарушение" этой алгоритмичности, которое также связано с локальной неустойчивостью и хаосом; · логистичность; · нечеткость, · многовариантность развития и протекания процессов.
Так, например, "память о прошлом" проявляется в симметрии статистических распределений вероятностей случайных событий, в их колебаниях за кратковременные и длительные интервалы времени. Как уже отмечалось выше, первые симметрия самоподобия (рекурсия) была обнаружена Б.Мандельбротом в биржевых котировках. Нечеткость - это проявление сочетания свойств статичности и динамичности. Алгоритмичность - это проявление необычных свойств, связанных с алгоритмическими "повторами" и изменениями в топологии, в очертаниях границ и в размерности фрактальных объектов. Границы имеют сложный, изрезанный характер, а размерность становится дробной. Под свойством "логистичности" фрактальных объектов мы понимаем следующее. Числовые последовательности, связанные с нелинейной фрактальной динамикой обнаруживают возможность проявления некого иного порядка следования,который, например, отличается от порядка следования действительных или комплексных чисел, получаемых в результате решения простейших и обычных алгебраических, дифференциальных или рекурсивных уравнений. Проявление свойств локальной неустойчивости и стохастичности взаимосвязаны – они вызваны "включением" в итеративный процесс стохастического фактора - хаоса. Будем исходить из того, что хаос всегда привносит в процессы нечто новое. Эту идею привнесения "нового" при рассмотрении фрактальных объектов и формирования "нового порядка" из хаоса впервые высказал нобелевский лауреат Илья Романович Пригожин[20]. Даже в известном кинофильме "Матрица" одна из героинь – Пифия произносит такую фразу: "déjà vu" дает все новую и новую информацию...".
А ведь при нашем рассмотрении, "déjà vu" – это итерационный процесс и "новое" в немявляетсяследствием проявления, стохастичности и хаоса. В качестве примера проявления свойств "логистичности" рассмотрим два набора из комплексных чисел. Пусть, например, заданы две колонки данных одинаковой размерности, состоящие из комплексных чисел К особым свойствам фрактальных объектов следует отнести многовариантность развития и одновременного протекания во времени сразу нескольких процессов. В динамике нелинейных стохастических процессов, происходящих во фрактализованных диссипативных структурах и средах, потенциально возможны любые исходы развития и протекания. Это является следствием их сильной нестабильности и локальной неустойчивости. При этом развитие и протекание процессов может идти по различным схемам, - например, когда процесс "запускается" для какого-то одного из вариантов, или когда в схеме процесса одновременно "запущены" сразу несколько комбинаций или сочетаний вариантов из некого потенциально возможного многообразия. Поэтому при отображении организационно сложных фрактальных конгломератов к уровню реальных объектов и процессов должен учитываться выбор наиболее "возможного" варианта "цепочки" состояний из совокупности вариантов или состояний мета-уровня. Для понимания сущности этой "фрактальной многовариантности" приведем пример. Пусть приведенная выше графики - рис.1а и рис.1б - иллюстрируют специфику динамики фазовых траекторий с локальной неустойчивостью, - как без перепутывания траекторий Но вначале нам необходимо сделать ряд дополнительных построений на этих рисунках: -1) добавим на них систему координат, -2) на горизонтальной оси времени отложим интервалы значений
без запутывания траек- Запутывание фазовых траекторий это - торий. следствие выполнения закона "сохранения площади фазовой капли во времени".
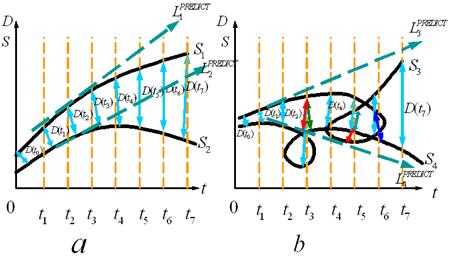
Рис. 14. а) Локальная неустойчивость. б) Более сильная локальная неустойчивость. без запутывания траек- Запутывание фазовых траекторий это - торий следствие выполнения закона "сохранения площади фазовой капли во времени". Рис.14 имеет ряд особенностей в виде "петель"[21], на которые надо обратить особое внимание. Возникновение петель на фазовых траекториях свидетельствует о том, что их локальная неустойчивость является более сильной. Более того, эти петли могут иметь на фазовых портретах многократный циклический характер. Касательные линии
Кривые фазовых траекторий
Учитывая, что характер каждой такой "кривой" - далеко не гладкий, а фрактальный, т. е. “изрезанный" и "шершавый", фактически, - суть этого свойства сводится к тому, что: внутри петли любая совокупность, например, состоящая из 2-х процессов с фазовыми траекториями
Мы не скрываем, что все эти наши "попытки" проведения такого анализа на основе интуиции должны быть учтены как при разработке модели кванторов фрактальной фазификации и дефазификации, так и.при моделировании итерируемого процесса. Не можем удержаться еще от одной ремарки, так как она связана с классификацией формируемых фракталов. Так, например, если бы мы для формирования фракталов использовали трансцендентные итерационные уравнения, то, очевидно, такой тип фракталов назывался бы трансцендентным. А если при формировании итерационного процесса в его уравнение входила функция предпочтения Выше мы уже отмечали, что при построении формальных систем широко используется так называемый формально-аксиоматический метод [22]. Мы применим этот метод для вывода вида уравнения процесса. Вначале мы определим ряд требований, а затем выполнив ряд преобразований, получим явное выражение для этого процесса.
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 301; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.205.92 (0.012 с.) |

 Математик раннего средневековья Фибоначчи[18] - широко известен по так называемым числам Фибоначчи, в основу которых положена рекурсивная зависимость
Математик раннего средневековья Фибоначчи[18] - широко известен по так называемым числам Фибоначчи, в основу которых положена рекурсивная зависимость  для целых чисел, которая формирует последовательность 1, 1, 2, 3, 5, 8, 13, 21, 34, 55....
для целых чисел, которая формирует последовательность 1, 1, 2, 3, 5, 8, 13, 21, 34, 55....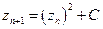 для итеративного рекурсивного процесса на комплексной плоскости и порождения фрактала Мандельброта. И если рассуждать по аналогии с так называемыми известными числами Фиббоначчи, то можно сказать, что фрактал Мандельбротта состоит из " чисел Мандельбротта ".
для итеративного рекурсивного процесса на комплексной плоскости и порождения фрактала Мандельброта. И если рассуждать по аналогии с так называемыми известными числами Фиббоначчи, то можно сказать, что фрактал Мандельбротта состоит из " чисел Мандельбротта ". -ой степени. рассматриваемых на комплексной плоскости. Третий тип - тип стохастических фракталов - учитывает свойство самоподобия в "картинках" распределения экспериментальных вероятностей случайных событий.
-ой степени. рассматриваемых на комплексной плоскости. Третий тип - тип стохастических фракталов - учитывает свойство самоподобия в "картинках" распределения экспериментальных вероятностей случайных событий.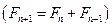 , или - чисел фрактала Мандельброта
, или - чисел фрактала Мандельброта 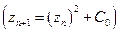 .
.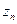 и комплексных величин функции принадлежности
и комплексных величин функции принадлежности 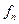 . Над ними можно выполнить операцию произведения и получить 3-й набор - из произведений
. Над ними можно выполнить операцию произведения и получить 3-й набор - из произведений 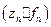 . Нетрудно догадаться, что порядок чисел в 1-ом
. Нетрудно догадаться, что порядок чисел в 1-ом 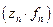 -наборе будут отличаться друг от друга.
-наборе будут отличаться друг от друга.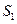 ,
, 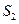 , так и траекторий
, так и траекторий 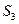 ,
, 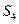 , в которых локальная неустойчивость более сильна и имеют место перепутывание траекторий и образование
, в которых локальная неустойчивость более сильна и имеют место перепутывание траекторий и образование 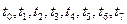 , -3) отложим на траекториях для этих моментов времени инкременты
, -3) отложим на траекториях для этих моментов времени инкременты 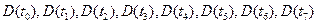 . Результаты этих построений отражены на рис.13.
. Результаты этих построений отражены на рис.13.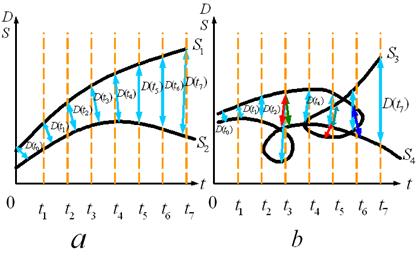
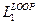 и
и 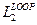 к траектории
к траектории 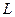 при "вхождении" траектории
при "вхождении" траектории 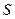 в петлю (пусть даже в виде самой "грубой" линейной формы – направления линии
в петлю (пусть даже в виде самой "грубой" линейной формы – направления линии 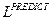 ) становится невозможным. Интервал времени
) становится невозможным. Интервал времени 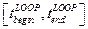 , на котором "сидит" петля фазовой траектории
, на котором "сидит" петля фазовой траектории 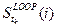 , характеризуется также и новым свойством:
, характеризуется также и новым свойством: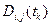 проявляют в петлях вид многозначный зависимости. Поэтому для каждого отдельного момента времени
проявляют в петлях вид многозначный зависимости. Поэтому для каждого отдельного момента времени 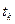 внутри интервала
внутри интервала 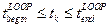 на кривых в петле можно определить более 2-х различных направлений касательных
на кривых в петле можно определить более 2-х различных направлений касательных 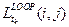 , а, следовательно, для каждого такого момента времени
, а, следовательно, для каждого такого момента времени 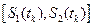 , формирует "пучёк" взаимодействующих друг с другом подпроцессов с целым "веером"направлений касательных
, формирует "пучёк" взаимодействующих друг с другом подпроцессов с целым "веером"направлений касательных  .
. (в качестве одного из факторов), то такой фрактал мы вправе назвать "логистическим". Это мы попытаемся использовать при выводе уравнения итерационного процесса ниже.
(в качестве одного из факторов), то такой фрактал мы вправе назвать "логистическим". Это мы попытаемся использовать при выводе уравнения итерационного процесса ниже.


