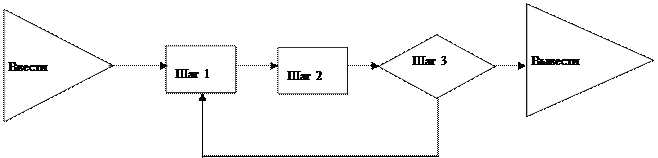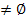Основная гипотеза теории алгоритмов.

 

Любая практическая задача, приводящая к необходимости создания эффективного вычислительного метода (алгоритма), может быть поставлена в точных математических терминах.

Эта парадигма (гипотеза, принцип) применительно к уточнению понятия алгоритм, как абстрактной машины известно, в виде тезиса Тьюринга: «Для всякого алгоритма S_f в каком-либо алфавите может быть построен тьюриноговский алгоритм, дающий при одинаковых исходных данных, те же самые результаты, что и алгоритм S_f».

Принятие тезиса Тьюринга равносильно принятию тезиса Черча (для частично-рекурсивных функции) или принцип нормализации (для нормальных алгорифмов).

В настоящее время широко используется в теории алгоритмов тезис Черча-Тьюринга: «Любая теоретически разрешимая вычислительная задача может быть решена при помощи машины Тьюринга».

 

Формальные модели, уточнение понятия алгоритм.

 

Приведенное выше «наивное» (интуитивное) понятие алгоритма как первичное (исходное) понятие математики не допускает его определения в терминах более простых понятий. Возможные уточнения понятия алгоритма приводят, строго говоря, к известному сужению этого понятия. Каждое такое уточнение состоит в том, что для каждого из семи параметров алгоритма точно описывается некоторый класс, в пределах которого этот параметр может меняться.

 

Поскольку семь параметров однозначно определяют некоторый алгоритм, то выбор семи классов изменения этих параметров определяет некоторый класс алгоритма, то выбор семи классов изменения этих параметров определяет некоторый класс модели алгоритма, или алгоритмической системы (модели):

 

 

В настоящее время среди математических моделей алгоритмов описанного типа наиболее известными являются уточнения, предложенные А.М.Тьюрингом, А.А.Марковым, А.Черчем.

 

Эти алгоритмические модели, сводимые друг к другу, позволяют заменить неточные утверждения о существовании эффективных процедур (алгоритмов) точными утверждениями о существовании соответствующей алгоритмической системы (например, машины Тьюринга). С другой стороны, утверждения о невозможности построения алгоритмической системы для решения поставленной задачи следует истолковывать как утверждение о несуществовании алгоритма вообще.

 

Блок-схемы детерминированных алгоритмов.

 

Связи между шагами конструктивного процесса можно задать вершинно-взвешенным орграфом (блок-схемы), вида:

 

 

 

где вершинам соответствуют шаги (блоки), а дугам – переходы между шагами. Его вершины могут быть двух видов – операторы (из этих вершин выходит одно ребро) и предикаты (или логические условия; из этих вершин выходят два ребра). Кроме того, выделяют операторы начала и конца алгоритма.

В подобных схемах шаги могут быть элементарными или могут представлять собой самостоятельные алгоритмы (блоки).

На блок-схеме хорошо видна разница между описанием алгоритма и процессом его реализации.

Описание – это граф; процесс реализации – это путь в графе. Различные пути в одном и том же графе возникают при различных данных, которые создают разные логические условия в точках разветвления.

Отсутствие сходимости алгоритма означает, что в процессе вычисления не появляются условий, ведущих к концу, и процесс идет по бесконечному пути (зацикливается).

Отметим, что блок-схема отражает связи по управлению (что делать в следующий момент, то есть какому блоку передать управление), а не по информации (где этому блоку брать исходные данные).

Очевидно, что блок-схемы являются средством описания детерминизма алгоритма.

 

Замечания:

На практике блок-схемы часть имеют предикаты (точки разветвления) не только двоичные, но и многозначные, важно лишь, чтобы верным был, ровно один из возможных ответов.

Примечание:

Блок схема вида:

 

 

где блок А₁ вычисляют функцию f₁(x), а исходными данными для А₂ являются результаты А₁, называется композицией алгоритмов А₁ и А₂ (то есть эта блок-схема задает алгоритм, вычисляющий f₂(f₁(x)), то есть композицию f₁ и f₂)

 

 

Алгоритмический язык

 

Алгоритмический язык L = <A, S₁, S₂> предназначен для записи алгоритмов и при этом

Некоторый подалфавит В алфавита А используется для кодирования исходной информации.

Алгоритмический язык называется универсальным, если он содержит алгоритмически полный набор предписаний. Задание универсального алгоритмического языка равносильно заданию алгоритмической системы, т.е. общего способа записи алгоритма.

Языки, с помощью которых строятся алгоритмические системы (абстрактные машины, рекурсивные функции, нормальные алгорифмы), являются универсальными и ориентированы на рассмотрение фундаментальных теоретических вопросов теории алгоритмов.

В этом плане алгоритмические языки являются теоретической основой языков программирования.