
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Московский государственный институт электроники и математикиСтр 1 из 4Следующая ⇒
Московский государственный институт электроники и математики (Технический университет) Маркин П.М. Дискретная математика Теория алгоритмов Для студентов специальности "Вычислительные машины, комплексы, системы и сети" Учебный год Содержание: Общие положения. 3 Теория алгоритмов. 3 Абстрактная теория алгоритмов. 3 Метрическая теория алгоритмов. 3 Предмет и содержание читаемого курса. 5 Предмет изучения. 5 Цель. 5 Содержание курса. 5 Исходные понятия теории алгоритмов. 5 Алгоритм.. 5 Конструктивный объект. 5 Свойства и параметры алгоритма: 6 Основная гипотеза теории алгоритмов. 7 Формальные модели, уточнение понятия алгоритм. 7 Блок-схемы детерминированных алгоритмов. 8 Алгоритмический язык. 9 Алгоритмическая система А.Тьюринга. 9 а. Разрешимость и неразрешимость языков машиной Тьюринга. 10 б. Проблема остановки машины Тьюринга. 10 Алгоритмическая система А.Чёрча. 11 a. Базисные функции. 11 1. Нуль-функция. 11 2. Функция тождества. 12 3. Функция следования. 12 б. Операторы построения производных рекурсивных функций. 12 1. Оператором суперпозиции(подстановки) 12 2. Оператором примитивной рекурсии. 12 3. Оператор минимизации (m- оператор) 13 Примитивно-рекурсивные функции. 14 Алгоритмическая система А.А.Маркова. 15 Ассоциативное исчисление. 17 Алгоритмически неразрешимые проблемы. 18 Теоремы алгоритмически разрешимых и неразрешимых проблем. 19 Теоремы Геделя. 19 I. Теорема о неполноте. 19 II. Теорема о полноте. 19 Словарь основных терминов. 21 ТЕОРИЯ АЛГОРИТМОВ.
Общие положения.
Теория алгоритмов - раздел математической логики, в котором изучаются теоретические возможности эффективных процедур вычисления (алгоритмов) и их приложения. Основное понятие этой теории – алгоритм – в интуитивном (наивном) понимании существует в математике довольно давно, а точные математические понятия, которые в том или ином смысле формализуют интуитивное понятие алгоритма, предложены только в середине 30-х годов 20-го века. Необходимость такой формализации была обусловлена как вопросами обоснования математики, так и вопросами доказательства алгоритмической разрешимости и неразрешимости тех или иных задач. Очевидно, что в математике доказываемый объект должен быть точно формализован.
В настоящее время теорию алгоритмов делят на дескриптивную (абстрактную) и метрическую (структурную, прикладную). Абстрактная теория алгоритмов исследует алгоритмы с точки зрения устанавливаемого ими соответствия между исходными данными и результатами; к ней относятся, в частности, проблемы построения алгоритма, обладающего теми или иными свойствами, - алгоритмические (массовые) проблемы (т.е. нахождение единого метода решения бесконечной серии однотипных единичных задач). q = <M1, M2, Sf>, где M1 -множество возможных исходных данных, M2 – множество возможных результатов применения алгоритма Sf к M1:
Пример: f2 : N2 →N, где f2 – операция сложения чисел N. В этом случае M1 = N2 = Domf2, M2 = N
Метрическая теория алгоритмов исследует алгоритмы с точки зрения сложности, как самих алгоритмов, так и задаваемых ими вычислений, т.е. процессов последовательного преобразования конструктивных объектов.
Замечание: 1. Абстрактная теория алгоритмов не учит строить конкретные алгоритмы. Этим занимается прикладная (метрическая) теория алгоритмов.
2. Ниже изучаются сводящиеся друг к другу теоретические модели алгоритмов из 3 классов формальных систем F.S = <L, D>: - алгоритм рассматривается как исключение формул (рекурсивные функции); - алгоритм, как гипотетически вычислимое устройство (машины Тьюринга (МТ)); - алгоритм есть конечный набор правил подстановки слов (нормальные алгорифмы)
3. Проблемы построения алгоритма, обладающего теми или иными свойствами. Называется массовой (алгоритмической) проблемой. Если искомый алгоритм не существует, то говорят, что рассматриваемая массовая проблема неразрешима.
4. В отличие от абстрактной теории алгоритмов прикладная теория рассматривает не только детерминированные, но также вероятностные (стохастические) и эвристические алгоритмы. В последнем случае, кроме детерминированных или статически заданных правил, алгоритм включает также содержательные указания о целесообразном направлении процесса.
5. Любой алгоритм Sf однозначно сопоставляется исходным данным (если DomSf ≠ Ø) результат. Это означает, что с каждым алгоритмом Sf однозначно связана функция f, которую алгоритм Sf вычисляет. Однако обратное утверждение неверно (т.е. существуют невычислимые функции).
6. Доказательством существования алгоритма Sf вычисления функции f не означает описание этого алгоритма. Так, например, функция
f (x) = 1, если теорема Ферма верна, 0, если теорема не верна,
вычислима, т.к. она равна либо функции, тождественно равной 1, либо функции, тождественно равной 0, а обе эти функции вычислимы.
7. f DomSf (x) = 1, если x не принадлежит DomSf, 0, если x принадлежит DomSf, вычислима. В этом плане говорят о разрешающем алгоритме Sf на множестве исходных данных М1.
Аналогично, ImSf есть перечислимое (рекурсивно-перечислимое) множество, т.к. оно является областью значений рекурсивной функции f с областью определения DomSf. Для множества ImSf алгоритм Sf есть порождающий для М1.
Предмет изучения в читаемом курсе - формальные уточнения интуитивного понятия «алгоритм» с различных точек зрения: арифметизации, нормализации и построения абстрактной машины. Цель читаемой дисциплины студентам специальности 2201 - усвоение необходимости формулировать алгоритмические проблемы как проблемы решения вопроса о существовании алгоритма для решения данной бесконечной серии однотипных задач и нахождение такого алгоритма в случае, если он существует.
Содержание курса - математические модели алгоритмических систем, формы их записи и оценки сложности алгоритмов. В этом аспекте изучаются: - рекурсивные функции как математический вариант уточнения понятия вычислимой арифметической функции f: Nn→ N; - машины Тьюринга как математический эквивалент для общего интуитивного представления об алгоритме; - системы подстановок слов в заданном алфавите;
Исходные понятия теории алгоритмов. Алгоритм (алгорифм) – точное предписание, которое задает вычислительный процесс (называемый в этом случае алгоритмическим), начинающийся с произвольного исходного данного(из некоторой совокупности возможных дл данного алгоритма исходных данных) и направленный на получение полностью определенного этим исходным данным результата.
Примеры: «Проезд запрещен», «Не курить» - не алгоритмы; «Придерживайтесь правой стороны», «Место для курения», «Вход» - не алгоритмы; Сложение (умножение, вычитание, деление) двух чисел (т.е. N2®N) столбиком – алгоритм.
Пример: Упорядочить в порядке возрастания конечное множество М положительных чисел. Описание решения этой задачи в интуитивном смысле может быть: Шаг 1: В М ищется наименьшее число Шаг 2: Найденное число приписывается справа к возрастающей последовательности чисел R (в начальный момент R пусто) и вычеркивается из М; Шаг 3: Если в М не осталось чисел, то перейти к шагу 4, в противном случае перейти к шагу 1; Шаг 4: Конец. Результатом считать последовательность R, построенную к данному моменту. Это описание, которое кажется вполне ясным, далеко от алгоритма. Действительно, если М=í9Ö5, 6Ö2, (1/3)p/2ý, то в предложенном варианте решения поставленной задачи не указано, как искать наименьшее число.
Этот пример показывает, что понятие алгоритма в интуитивном смысле требует уточнения понятия данных (т.е. указать каким требованиям должны удовлетворять объекты, чтобы алгоритмы могли с ними работать), памяти, дискретности, элементарности, конечности числа шагов, направленности, детерминированности, результативности, массовости.
Конструктивный объект – объект формальной системы F.S = <L, D> = <A, S, Ax, R>, где L – формальный язык, D – дедуктивные средства конструктивного процесса построения конструктивных объектов, Ax – аксиомы(исходные данные), Ax принадлежит L, R – отношения на множестве объектов(продукции, правила вывода, правила построения объектов) исходных объектов. Пример: Простейшим видом конструктивных объектов являются слова в фиксированном алфавите А, т.е. цепочки букв этого алфавита. В этом случае буквы являются исходными объектами, а конструктивный процесс состоит в данном случае в выписывании этого слова буква за буквой. Так, натуральные числа, рассматриваемые как слова в алфавите A={0, 1} начинающиеся с нуля и не содержащие других вхождений нуля, т.е. как слова 0, 01, 011, 0111… Очевидно, что рациональные числа также являются конструктивными объектами в алфавите{0, 1, -, /}.
Пример: Формальный язык – конструктивный объект, лексемы которого строятся из букв заданного алфавита с привлечением заданной формальной грамматики.
Замечание: Формальная система F.S., обладающая свойствами элементарности и дискретности шагов построения конструктивных объектов, может служить формальной моделью алгоритма в интуитивном смысле. Детерминированная формальная система F.S. является формальной моделью алгоритма в абстрактной теории алгоритмов.
Пример: Машина Тьюринга <A, Q,
Здесь детерминированность означает, что к каждой конфигурации Машины
Примечание: Исходные данные алгоритма в дальнейшем формализуются как слова в алфавите этих данных. Аналогично формализуются промежуточные и выходные (т.е. результат) данные.
Свойства и параметры алгоритма: Из неформального определения понятия «алгоритм» следуют его характеристические свойства: - дискретность (каждый конструктивный объект получается из предыдущих по определенному правилу конструктивного процесса) - направленность(все конструктивные объекты, как множества, упорядочены) - детерминированность (однозначность выбора правил построения конструктивных объектов) - Элементарность шагов (отсутствует необходимость уточнения правил конструктивного процесса) - массовость (инвариантность относительно входных данных; уточнения понятия решения задачи в общем виде) - результативность (получение требуемого конструктивного объекта по окончанию конструктивного процесса)
Очевидно, что характеристикой алгоритма является совокупность тех его свойств, которые определяют его возможности: быстродействие, производительность и т.д.
Замечание:
1. Алгоритм Sf не применим к исходному данному, если конструктивный процесс не заканчивается или заканчивается безрезультатно 2. Следует различать: - Описание алгоритма как инструкции (программы), - Система реализации алгоритма, - Процесс реализации алгоритма (конструктивный процесс), - Сходимость процесса реализации алгоритма (результативная остановка после конечного числа шагов алгоритма), - Строение алгоритмического процесса (наличием или отсутствием промежуточных результатов). В свете изложенного 7 параметров однозначно характеризуют данный алгоритм: - совокупность возможных исходных данных, - совокупность возможных результатов, - совокупность возможных промежуточных результатов, - правило начала, - правила конструктивного процесса. - правило окончания. - правило извлечения результата.
Алгоритмический язык
Алгоритмический язык L = <A, S1, S2> предназначен для записи алгоритмов и при этом Некоторый подалфавит В алфавита А используется для кодирования исходной информации. Алгоритмический язык называется универсальным, если он содержит алгоритмически полный набор предписаний. Задание универсального алгоритмического языка равносильно заданию алгоритмической системы, т.е. общего способа записи алгоритма. Языки, с помощью которых строятся алгоритмические системы (абстрактные машины, рекурсивные функции, нормальные алгорифмы), являются универсальными и ориентированы на рассмотрение фундаментальных теоретических вопросов теории алгоритмов. В этом плане алгоритмические языки являются теоретической основой языков программирования.
Теорема. «Не существует алгоритма распознавания остановки произвольной МТ для произвольной начальной её конфигурации».
Замечание: Известны два способа доказательства неразрешимости той или иной массовой проблемы: прямой (основанный на так называемом «диагональном» методе) и косвенный (использующий сводимость к данной проблеме другой массовой проблеме, неразрешимость которой была доказана раньше).
A. Базисные функции Базисные (простейшие элементарные) функции – числовые вычислимые функции
Примеры:
Примеры:
Примеры:
Замечание: базисные функции имеют значения только для заданных значений их аргументов.
Пример. Функция f(x1,…, xn) возникает из функций h(x1,…, xm), g1(x1,…, xn), …gm(x1,…, xn) суперпозицией, если f(x1,…, xn)= Snm(h, g1,…, gm) = h(g1(x1,…, xn), …, gm (x1,…, xn)). Если заданы функции Jnm и операторы Snm, то можно считать заданными всевозможные операторы подстановки функции в функцию, а также переименования, перестановки и отождествления переменных. Так, если f(x1, x2)= h(g1(x1, x2), g2(x1)), то ее стандартный вид следующий: f(x1, x2)= S22(h(x1, x2), g1 (x1, x2), S12 (J21(x1, x2), g2(x1), g3(x1))), где g3 – любая функция от х1. Если же имеем f(x2, x1, х3, …, xn) и f(x1, x1, x3,…, xn), то пишем: f(x2, x1, х3, …, xn) = f(J22(x1, x2), J21(x1, x2), х3, …, xn), f(x1, x1, x3,…, xn)= f(J21(x1, x2), J21(x1, x2), х3, …, xn).
Пример:
2. Оператором примитивной рекурсии Rn[f1n-1,f2n+1,x1(n)]=fmn называется процесс определения функции f (n+1) переменных через n-местную функцию g и (n+2)- местную функцию h в следующем виде: f(x1, x2, …, xn, 0)= g(x1, x2,…, xn) f(x1, x2, …, xn, y+1)=h(x1, x2,…, xn, y, f(x1, x2, …, xn, y)), где g и h – две различные функции соответственно n и n+2 аргументов. Эта пара равенств называется схемой примитивной рекурсии. Тот факт, что функция f определена схемой примитивной рекурсии выражается равенством f(x1, x2, …, xn, y)=Rn(g, h). В случае, когда n=0, то есть определяемая функция f является одноместной, схема примитивной рекурсии принимает более простой вид: f(0)=с, f(у+1)=h(y, f(y)), где с – константа.
Схема примитивной рекурсии определяет f рекурсивно не только через другие функции g и h, но и через значения f в предшествующих точках: значение функции f в точке у+1 зависит от значения функции f в точке у. Очевидно, что для вычисления f(x1,…, xn, k) понадобиться k+1 вычислений по схеме примитивной рекурсии – для у=0, k.
Замечания: Существенным в операторе примитивной рекурсии Rn является то, что независимо от числа переменных в f рекурсия ведется только по одной переменной у (остальные n переменных x1, x2, …, xn на момент применения схемы примитивной рекурсии зафиксированы и играют роль параметров).
3. Оператор минимизации (m- оператор). Оператором минимизации m (наименьшего числа оператора) называется преобразование (n+1)-местной функции (в общем случае частичной) j в n-местную f, такую, что для любых х1, х2, …хn, у равенство f(х1, х2, …хn)=у имеет место лишь в том случае, если определены и не равны нулю значения j(х1, …, хn, 0), …, j(х1, …, хn, у-1) и при этом j(х1, х2, …хn, у)=0. Применение оператора минимизации обозначают m[j, (y)], где у - исчезающий аргумент.
Говорят, что n-местная арифметическая функция f: Nn®N получается из функции j: Nn+1®N с помощью m-оператора, если выполнено условие: для любых k1, k2,…, kn, kÎN. f(k1, k2,…, kn)=k, тогда и только тогда, когда для всех l<k значения j(k1, k2,…, kn, l) определены и отличны от нуля, а значение j(k1, k2,…, kn, k) определено и равно нулю. Если f получается из функции j с помощью оператора наименьшего числа m, то пишут: f(x1, x2,…, xn)=my[j(x1,…, xn, y)=0].
Важным свойством m-оператора является то, что с его помощью из вычислимой функции jвсегда получается частичная вычислимая функция f. Именно, если имеется алгоритм для вычисления j, то значение f(x1, x2,…, xn) может вычисляться следующим образом: вычисляется j(x1, x2,…, xn, 0); если процесс вычисления закончился, то есть значение j(x1, x2,…, xn, 0) определено, и j(x1, x2,…, xn, 0)=0, то полагаем f(x1, x2,…, xn)=0, а если j(x1, x2,…, xn, 0)¹0, то начинают вычислять j(x1, x2,…, xn, 1). Если процесс вычисления закончился и j(x1, x2,…, xn, 1)=0, то полагают f(x1, x2,…, xn)=1, а если j(x1, x2,…, xn, 1)¹0, то переходят к вычислению j(x1, x2,…, xn, 2) и так далее. Процесс вычисления закончится, если найдется такое у, что для всех z < y значение j(x1, x2,…, xn, z) определено и отлично от нуля, а j(x1, x2,…, xn, у) определено и равно нулю. Тогда f(x1, x2,…, xn) = у.
Пример: f(x)=my[12*y-x½=0]. Тогда f(x)=x/2 при всех четных значениях хÎN. Замечание: Примитивно-рекурсивные функции всегда определены (имеют значения) для любых значений аргументов. Иначе обстоит дело с функциями, полученными при помощи m-оператора. Для некоторых комбинаций значений аргументов они могут быть не определены, потому что исходная функция не принимает нулевых значений. Пример: det f(x)=m[J21(x, y), (y)]. Полученная функция f(х) обладает следующими свойствами: f(0)=0, f(k) не существует при k¹0. Последнее означает, что для заданной функции J21(x, y) m-оператор не может построить f(k) kÎN, так как при x=k функция j(x, y)= J21(x, y) ни для какого значения у не будет равной нулю.
Ассоциативное исчисление Ассоциативное исчисление (система Туэ) U – формальная система F.S., задающая конечно определенные ассоциативные системы (полугруппы) Ku. Всякое ассоциативное исчисление U=<A, Σ> определяется указанием некоторого алфавита A и конечного списка Σ соотношений в A – пар слов в этом алфавите αi↔βi. Пара αi→βi понимается как левая подстановка, а βi→αi – как правая постановка в заданное слово αÎA*=eÈAÈA∙AÈ…ÈAkÈ…(kÎN; e – пустое слово). Допустимым относительно списка Σ действием над словами в алфавите A называется любая подстановка одной из частей какого-либо соотношения αi↔βi ((αi↔βi)ÎΣ) вместо вхождения другой части того же соотношения. Ассоциативное исчисление U=<A, Σ> представляет собой разрешение производить, исходя из любого слова RÎA*, любые допустимые относительно списка Σ действия.
Пример: Подстановка ab↔bcb применима четырьмя способами к слову P1=abcbcbab: замена каждого из двух вхождений bcb даст слова aabcbab и abcabab, а замена каждого из двух вхождений ab дает слова bcbcbcbab и abcbcbbcb. В то же время к слову P2=bacb эта подстановка не применима, а подстановка вида α↔e означает, что из преобразуемого слова PiÎA* выбрасывается вхождение слова α, а также что между двумя какими-либо буквами преобразуемого слова или впереди него, или за ним вставляется слово α (e-пустое слово, eÎA*, eÏA). Обо всех словах Q, которые при этом получаются (в том числе и о самом исходном слове P), говорят, что они эквивалентны P в ассоциативном исчислении U=<A,Σ> (в символической записи U:P╨Q). Отношение ╨ для любого ассоциативного исчисления U рефлексивно, симметрично и транзитивно. Кроме этого, из U:P1╨Q и P2╨R следует, что U: P1P2╨QR. Это позволяет естественным образом сопоставить всякому ассоциативному исчислению U некоторую конечно определенную ассоциативную систему Ku, взяв в качестве ее элементов классы слов, эквивалентных друг другу в U=<A, Σ>, а в качестве операции умножения в Ku – операцию конкатенации слов в алфавите A. Так настроенная ассоциативная система Ku будет моноидом, т.е. будет иметь нейтральный элемент eÎA*; элементы Ku представленные буквами алфавита A, будут составлять для Ku систему порождающих элементов, а список соотношений Σ будет представлять собой полную систему соотношений между упомянутыми порождающими элементами Ku в том смысле, что элементы Ku, представленные словами P и Q, тождественны в Ku тогда и только тогда, когда P и Q эквивалентны в U=<A, Σ>. В этом плане, распознавание тождества элементов в Ku сводится распознаванию эквивалентности слов в U=<A, Σ>. Отсюда понятна важность исследования разрешимости алгоритмической проблемы распознавания эквивалентности слов в произвольном ассоциативном исчислении. Эта проблема состоит в том, что для произвольного U=<A, Σ> требуется построить алгоритм, который для любой пары слов в алфавите A U=<A, Σ> позволял бы за конечное число шагов выяснить, эквивалентны ли в U=<A, Σ> слова, составляющие эту пару. В алгебраической интерпретации эта проблема есть проблема тождества для полугруппы Ku.
Теорема (Маркова-Поста): “Существует ассоциативное исчисление, в котором проблема распознавания эквивалентности слов алгоритмически неразрешима”
Действительно, рассматривая машину Тьюринга как математическую модель алгоритма, можно свести проблему распознавания эквивалентности слов в U=<A, Σ> к проблеме остановки машины Тьюринга (а эта проблема является алгоритмически неразрешимой).
Приведем и следующие две теоремы: “Для любого перечислимого множества M существует система подстановок, множество заключительных слов которой совпадает с M” “В ассоциативном исчислении два слова эквивалентны, если им соответствуют две конфигурации машины Тьюринга такие, что за конечное число тактов машина переходит из первой конфигурации ко второй”
Очевидно, что теорема: “Существует полугруппа заданная определяющими соотношениями, в которой проблема распознавания эквивалентности (равенства) слов алгоритмически неразрешима” является переформулировкой теоремы Маркова-Поста. Примером ассоциативного исчисления с неразрешимой проблемой равенства является исчисление U=<{a,b,c,d,e},{ac↔ca, ad↔da, bc↔cb, bd↔db, abac↔abace, eca↔ae, edb↔be}>
Замечание: к проблеме эквивалентности слов в ассоциативном исчислении сводятся многие задачи математики.
Так, любую формулу соответствующего языка математики можно рассматривать как слово в известном алфавите. Процесс эквивалентных преобразований или вывод в таком случае есть преобразование слов с привлечением тех или иных подстановок, в качестве которых выступают аксиомы, тождества, законы.
Теоремы Геделя. I. Теорема о неполноте
Эта теорема Геделя обычно рассматривается как следующие два утверждения: 1. «В любой непротиворечивой формальной теории, содержащей формальную арифметику, найдется формально неразрешимое суждение, т.е. такая замкнутая формула А, что ни А, ни ┐А не являются выводимыми в этой теории». 2. «Для любой непротиворечивой формальной теории, содержащей формальную арифметику, формула А, выражающая непротиворечивость теории, недоказуема в теории». II. Теорема о полноте Эта теорема является утверждением о полноте классического И.П: «Всякая предикатная формула, истинная во всех моделях выводима (по формальным правилам классического исчисления предикатов)».
Примечание: 1. Согласно теореме Геделя о неполноте арифметика и теория чисел оказываются неаксиоматизируемыми теориями (множество всех истинных высказываний арифметики не перечислимо). Это означает, что для достаточно богатых математических теорий не существует адекватных формализаций, а также невозможность исследования метасвойств теории средствами самой формальной теории.
2. Теорема Геделя о полноте утверждает перечислимость множества всех истинных высказываний логики предикатов.
3. Согласно теореме Черча классическое исчисление предикатов неразрешимо. В этом плане, не смотря на полноту И.П. разрешающей процедуры, связанной с вычислением значений истинности предикатных формул, построить не удается из-за бесконечности предметной области (это приводит в общем случае к бесконечным таблицам истинности). 4. Исчисление высказываний разрешимо и полно. Разрешающий алгоритм для всех формул F И.В. заключается в вычислении значений F на всех наборах значений её переменных. В виду полноты И.В. F является его теоремой, если и только если она истинна на всех своих наборах.
Словарь основных терминов.
Теория алгоритмов - раздел математической логики, в котором изучаются теоретические возможности эффективных процедур вычисления (алгоритмов) и их приложения.
Массовая (алгоритмическая) проблема - проблема построения алгоритма, обладающего теми или иными свойствами.
Алгоритм (алгорифм) – точное предписание, которое задает вычислительный процесс (называемый в этом случае алгоритмическим), начинающийся с произвольного исходного данного(из некоторой совокупности возможных дл данного алгоритма исходных данных) и направленный на получение полностью определенного этим исходным данным результата.
Конструктивный объект – объект формальной системы F.S = <L, D> = <A, S, Ax, R>, где L – формальный язык, D – дедуктивные средства конструктивного процесса построения конструктивных объектов, Ax – аксиомы(исходные данные), Ax принадлежит L, R – отношения на множестве объектов(продукции, правила вывода, правила построения объектов) исходных объектов.
Формальный язык – конструктивный объект, лексемы которого строятся из букв заданного алфавита с привлечением заданной формальной грамматики.
Алгоритмический язык L = <A, S1, S2> предназначен для записи алгоритмов и при этом
Алгоритмические процессы – процессы, которые могут имитироваться на подходяще построенной абстрактной машине, описываемой в точных математических терминах
Тезис Тьюринга: «Для всякого алгоритма Sf в каком-либо алфавите может быть построен тьюриноговский алгоритм, дающий при одинаковых исходных данных, те же самые результаты, что и алгоритм Sf».
Тезис Черча-Тьюринга: «Любая теоретически разрешимая вычислительная задача может быть решена при помощи машины Тьюринга».
Машина Тьюринга (МТ) – алгоритмически полная система побуквенной обработки словарной информации. Эта гипотетическая машина является формой существования и записи алгоритма.
Рекурсивное (разрешимым) множество - множество слов, для которого МТ однозначно решает задачу принадлежности или не принадлежности данного слова языку, т.е. машина либо переходит в состояние qz1, соответствующее заключению о принадлежности слова языку, либо в состояние qz2 – слово не принадлежит языку.
Рекурсивно-перечислимое (частично-разрешимое) множество – такое множество, если МТ останавливается в заключительном состоянии для лексем (слов заданного алфавита) и «зависает» (зацикливается) или останавливается в состоянии qi
Тезис Черча: “Всякая функция, значение которой может вычисляться эффективно, является частично-рекурсивной” (т.е. вычислимыми функциями являются частично-рекурсивные функции – функции, получаемые за конечное число шагов из простейших с помощью суперпозиции, примитивной рекурсии и μ-оператора).
Базисные (простейшие элементарные) функции – числовые вычислимые функции
Нуль-функция Z (x1, x2,…,xk)=0 – k-арная функция (оператор аннулирования Z), соответствующий алгоритм вычисления которой: “Любой совокупности значений аргументов xi функции Z ставится в соответствие ее значение 0”.
Функция тождества
Функция следования
Оператором суперпозиции(подстановки) Snm называется операция подстановки в функцию от m переменных m функций от n переменных.
Оператором примитивной рекурсии Rn[f1n-1,f2n+1,x1(n)]=fmn называется процесс определения функции f (n+1) переменных через n-местную функцию g и (n+2)- местную функцию h в следующем виде: f(x1, x2, …, xn, 0)= g(x1, x2,…, xn) f(x1, x2, …, xn, y+1)=h(x1, x2,…, xn, y, f(x1, x2, …, xn, y)), где g и h – две различные функции соответственно n и n+2 аргументов. Эта пара равенств называется схемой примитивной рекурсии.
Оператором минимизации m (наименьшего числа оператора) называется преобразование (n+1)-местной функции (в общем случае частичной) j в n-местную f, такую, что для любых х1, х2, …хn, у равенство f(х1, х2, …хn)=у имеет место лишь в том случае, если определены и не равны нулю значения j(х1, …, хn, 0), …, j(х1, …, хn, у-1) и при этом j(х1, х2, …хn, у)=0
Базисные функции
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 415; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.170.183 (0.186 с.) |


 Множество DomSf есть разрешимое(рекурсивное) множество исходных данных алгоритма Sf, т.к. характеристическая функция
Множество DomSf есть разрешимое(рекурсивное) множество исходных данных алгоритма Sf, т.к. характеристическая функция >, как модель алгоритма, есть детерминированная формальная система, порождающая множество своих конфигураций (машинных слов – конструктивных объект, построенных из букв алфавита А ленты и алфавита Q внутренних состояний блока управления головкой):
>, как модель алгоритма, есть детерминированная формальная система, порождающая множество своих конфигураций (машинных слов – конструктивных объект, построенных из букв алфавита А ленты и алфавита Q внутренних состояний блока управления головкой):  ,
, 

 только одной команды из программы
только одной команды из программы 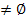
 , сопутствующие алгоритмы которых – одношаговые (очевидно, что это всюду определенные рекурсивные функции)
, сопутствующие алгоритмы которых – одношаговые (очевидно, что это всюду определенные рекурсивные функции)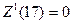 ;
;  ;
; 
 (x1, x2,…,xm,…,xn)= xm (
(x1, x2,…,xm,…,xn)= xm ( n).
n).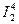 (7,6,1,4)= 6,
(7,6,1,4)= 6,  (6)= 6,
(6)= 6,  (7,15)= 15.
(7,15)= 15. (λ – оператор сдвига) – унарная функция, для которой: “Значением
(λ – оператор сдвига) – унарная функция, для которой: “Значением  принять натуральное число, следующее за числом, являющимся значением аргумента x ”.
принять натуральное число, следующее за числом, являющимся значением аргумента x ”.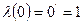 ;
;  .
.
 qz (безрезультатная остановка) для непринадлежащих языку слов.
qz (безрезультатная остановка) для непринадлежащих языку слов.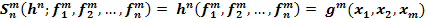 , а сопутствующий алгоритм которого: «Значения m –арных функций
, а сопутствующий алгоритм которого: «Значения m –арных функций  принять за значения аргументов n–арной функции
принять за значения аргументов n–арной функции  и вычислить её значение».
и вычислить её значение». для всех натуральных n, m, где n³m являются примитивно-рекурсивными;
для всех натуральных n, m, где n³m являются примитивно-рекурсивными;


