
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анализ трудоёмкости алгоритмовСодержание книги
Поиск на нашем сайте
Целью анализа трудоёмкости алгоритмов является нахождение оптимального алгоритма для решения данной задачи. В качестве критерия оптимальности алгоритма выбирается трудоемкость алгоритма, понимаемая как количество элементарных операций, которые необходимо выполнить для решения задачи с помощью данного алгоритма. Функцией трудоемкости называется отношение, связывающие входные данные алгоритма с количеством элементарных операций.
Трудоёмкость алгоритмов по-разному зависит от входных данных. Для некоторых алгоритмов трудоемкость зависит только от объема данных, для других алгоритмов — от значений данных, в некоторых случаях порядок поступления данных может влиять на трудоемкость. Трудоёмкость многих алгоритмов может в той или иной мере зависеть от всех перечисленных выше факторов.
Одним из упрощенных видов анализа, используемых на практике, является асимптотический анализ алгоритмов. Целью асимптотического анализа является сравнение затрат времени и других ресурсов различными алгоритмами, предназначенными для решения одной и той же задачи, при больших объемах входных данных. Используемая в асимптотическом анализе оценка функции трудоёмкости, называемая сложностью алгоритма, позволяет определить, как быстро растет трудоёмкость алгоритма с увеличением объема данных. В асимптотическом анализе алгоритмов используются обозначения, принятые в математическом асимптотическом анализе. Ниже перечислены основные оценки сложности.
Основной оценкой функции сложности алгоритма f(n) является оценка
если при g > 0 при n > 0 существуют положительные с1, с2, n0, такие, что:
при n > n0, иначе говоря, можно найти такие с1 и c2, что при достаточно больших n f(n) будет заключена между
В таком случае говорят еще, что функция g(n) является асимптотически точной оценкой функции f(n), так как по определению функция f(n) не отличается от функции g(n) с точностью до постоянного множителя. Например, для метода сортировки heapsort оценка трудоёмкости составляет
Из Важно понимать, что
Иначе говоря, запись Оценка
Например, запись Асимптотический анализ алгоритмов имеет не только практическое, но и теоретическое значение. Так, например, доказано, что все алгоритмы сортировки, основанные на попарном сравнении элементов, отсортируют n элементов за время, не меньшее
Поиск. Последовательный поиск Нахождение информации в неотсортированной структуре данных, например в массиве, требует применения последовательного поиска. Последовательный поиск - наиболее просто реализуемый метод поиска. Последовательный поиск заключается в последовательном просмотре массива от начального элемента до нахождения совпадения или до конца массива. Пример - циклы for и while. Последовательный поиск в среднем случае выполнит проверку 1/2*N элементов, в лучшем - 1 элемента, а в худьшем - N элементов. Недостаток - медленное выполнение при большом объеме просматриваемого массива. Но если данные не отсортированы, то должен использоваться только последовательный поиск. Двоичный поиск Бинарный поиск основан на итерационном сравнении ключа поиска со средним элементом массива. При каждой итерации интервал анализа делится пополам (на 2): 1/2, 1/4, 1/8 и т.д., откуда этот метод поиска и получил свое название. В зависимости от результата сравнения, выбирается нижний или верхний интервал. Процесс продолжается до тех пор, пока не будет найдено совпадение или длина интервала анализа не станет равной единице, и если при этом нет совпадения, то фиксируется неудача поиска. Этот метод поиска значительно эффективнее чем последовательный поиск, но требует, чтобы данные были предварительно упорядочены (отсортированы). В худшем случае выполняется не более log2(N)+E (где E<0.0861) сравнений, в связи с чем еще называется "логарифмическим поиском". Двоичный поиск также называется "дихотомическим".
Билет №20
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1903; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.124.119 (0.008 с.) |

 . Здесь n — величина объёма данных или длина входа. Мы говорим, что оценка сложности алгоритма
. Здесь n — величина объёма данных или длина входа. Мы говорим, что оценка сложности алгоритма

 и
и  .
. то есть g (n) = n log n
то есть g (n) = n log n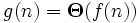 .
. представляет собой не функцию, а множество функций, описывающих рост
представляет собой не функцию, а множество функций, описывающих рост  с точностью до постоянного множителя.
с точностью до постоянного множителя. представляет собой верхнюю асимптотическую оценку трудоемкости алгоритма. Мы говорим, что
представляет собой верхнюю асимптотическую оценку трудоемкости алгоритма. Мы говорим, что  если
если
 задает нижнюю асимптотическую оценку роста функции f(n) и определяет класс функций, которые растут не медленнее, чем g(n) с точностью до постоянного множителя.
задает нижнюю асимптотическую оценку роста функции f(n) и определяет класс функций, которые растут не медленнее, чем g(n) с точностью до постоянного множителя. 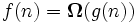 если
если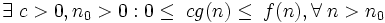
 обозначает класс функций, которые растут не медленнее, чем
обозначает класс функций, которые растут не медленнее, чем  , в этот класс попадают все полиномы со степенью большей единицы, равно как и все степенные функции с основанием большим единицы. Равенство
, в этот класс попадают все полиномы со степенью большей единицы, равно как и все степенные функции с основанием большим единицы. Равенство  .
.


