Алгоритмы сортировки. Априорная оценка сложности алгоритма. Сравнение эффективности различных алгоритмов сортировки. Особенности реализации.

Сортировки.

 

Пусть есть последовательность a0, a1... an и функция сравнения, которая на любых двух элементах последовательности принимает одно из трех значений: меньше, больше или равно. Задача сортировки состоит в перестановке членов последовательности таким образом, чтобы выполнялось условие: ai <= ai+1, для всех i от 0 до n.

 

Если значение функции сравнения зависит только от поля (элемента) x, то x называют ключом, по которому производится сортировка. На практике, в качестве x часто выступает число, а поле y хранит какие-либо данные, никак не влияющие на работу алгоритма.

 

Время сортировки - основной параметр, характеризующий быстродействие алгоритма.

Память - ряд алгоритмов требует выделения дополнительной памяти под временное хранение данных. При оценке используемой памяти не будет учитываться место, которое занимает исходный массив и независящие от входной последовательности затраты, например, на хранение кода программы.

Устойчивость - устойчивая сортировка не меняет взаимного расположения равных элементов.

Естественность поведения - эффективность метода при обработке уже отсортированных, или частично отсортированных данных. Алгоритм ведет себя естественно, если учитывает эту характеристику входной последовательности и работает лучше.

 

Сортировки:

1. Выбором.

Тупо выбираем наименьший(наибольший), просматривая всю не отсортированную часть, и пихаем его в конец (начало сортированной. Сложность – Сn². Память лишняя не нужна. Если входная последовательность почти упорядочена, то сравнений будет столько же, значит алгоритм ведет себя неестественно.

 

2. Пузырьком.

Проходим из конца массива в начало, по пути попарно меняя расставленные в неправильном порядке внутри пары элементы. После одного прохода один элемент отсортирован. После N проходов отсортированы все элементы. Доп. Память не требуется. Возможны улучшения (запоминать и не проверять отсортированную часть, «качели» - проход не в одном направлении, а в обоих последовательно), но они не изменяют сложность – Сn². Действует естественно.

 

3. Вставками

Похожа на пузырёк чем-то. Пусть есть отсортированная часть массива (в начале – первый элемент, массив из одного элемента - упорядочен). Добавим в него новый элемент – для этого аналогичным способом «просеем» его сквозь этот массив, пока не найден элемент, меньший x, или не достигнуто начало последовательности. Так добавим туда все элементы, массив отсортирован. Сложность – Сn². Действует естественно. Память не требуется.

 

4. Шелла

Модификация вставок. Массив делится пополам, и К-ый элемент первой части сравнивается с К-ым элементом второй части. Получаем набор упорядоченных пар, этот набор делится пополам и происходит аналогичная вышеописанной операция, причём каждый из упорядоченных массивов сливается в один методом вставок (в случае двух сортированных массивов это эффективный способ). Эта операция повторяется, пока массив не сортирован. Действует не естественно, сложность та же.

 

5. Пирамидальная.

Пирамида – бинарное дерево высоты k, все узлы имеют глубину k или k-1 (дерево сбалансированное), при этом уровень k-1 полностью заполнен, а уровень k заполнен слева направо; и выполняется "свойство пирамиды": каждый элемент меньше, либо равен родителю. Хранится он в виде массива. Соответствие между геометрической структурой пирамиды как дерева и массивом устанавливается по следующей схеме: 1) в a[0] хранится корень дерева, 2)левый и правый сыновья элемента a[i] хранятся, соответственно, в a[2i+1] и a[2i+2]. Дерево, не удовлетворяющее свойству пирамиды – это исходный, несортированный массив. Нужно построить из него пирамиду. Для этого начиная с нижнего элемента (последнего) выполняется операция просеивания: берётся его родитель и сравнивается с наибольшим из детей. Если больше, не трогаем. Если меньше, то меняем местами, и так делаем для всех родителей. Так, получаем пирамиду. Для выписывания сортированного массива берем верхний элемент пирамиды a[0]...a[n] (первый в массиве) и меняем с последним местами. Теперь "забываем" об этом элементе и далее рассматриваем массив a[0]...a[n-1]. Для превращения его в пирамиду достаточно просеять лишь новый первый элемент. Повторяем, пока обрабатываемая часть массива не уменьшится до одного элемента. Итог – сортированный массив. Построение пирамиды занимает Сn log n операций, причем более точная оценка дает даже Сn за счет того, что реальное время выполнения downheap зависит от высоты уже созданной части пирамиды. Вторая фаза занимает Сn log n времени: Сn раз берется максимум и происходит просеивание бывшего последнего элемента. Плюсом является стабильность метода: среднее число пересылок (n log n)/2, и отклонения от этого значения сравнительно малы. Пирамидальная сортировка не использует дополнительной памяти. Метод не является устойчивым: по ходу работы массив так "перетряхивается", что исходный порядок элементов может измениться случайным образом. Поведение неестественно: частичная упорядоченность массива никак не учитывается.

 

6. Быстрая(QSort)

· из массива выбирается некоторый опорный элемент a[i],

· запускается процедура разделения массива, которая перемещает все ключи, меньшие, либо равные a[i], влево от него, а все ключи, большие, либо равные a[i] - вправо,

· теперь массив состоит из двух подмножеств, причем левое меньше, либо равно правого,

для обоих подмассивов: если в подмассиве более двух элементов, рекурсивно запускаем для него ту же процедуру.

· В конце получится полностью отсортированная последовательность.

 

Каждое разделение требует Сn операций. Количество шагов деления (глубина рекурсии) составляет приблизительно log n, если массив делится на более-менее равные части. Таким образом, общее быстродействие: Сn log n, что и имеет место на практике. Однако, возможен случай таких входных данных, на которых алгоритм будет работать за Сn² операций. Такое происходит, если каждый раз в качестве центрального элемента выбирается максимум или минимум входной последовательности. Если данные взяты случайно, вероятность этого равна 2/n. И эта вероятность должна реализовываться на каждом шаге... Вообще говоря, малореальная ситуация. Метод неустойчив. Поведение довольно естественно, если учесть, что при частичной упорядоченности повышаются шансы разделения массива на более равные части. Сортировка использует дополнительную память, так как приблизительная глубина рекурсии составляет Сlog n, а данные о рекурсивных подвызовах каждый раз добавляются в стек.

 

7. Слияние

Рекурсивный метод – данный массив делится пополам, сортируется правая половина, сортируется левая половина, части сливаются. Глубина рекурсии – пока не получим массив из одного числа, который считается упорядоченным. Слияние двух отсортированных массивов по n элементов происходит за n операций(типа очевидно). Так – сложность

Сn log n, - результат весьма неплох, учитывая отсутствие "худшего случая". Однако, несмотря на хорошее общее быстродействие, у сортировки слиянием есть и серьезный минус: она требует n памяти. Хорошо запрограммированная внутренняя сортировка слиянием работает немного быстрее пирамидальной, но медленнее быстрой, при этом требуя много памяти под буфер. Поэтому mergeSort используют для упорядочения массивов, лишь если требуется устойчивость метода(которой нет ни у быстрой, ни у пирамидальной сортировок). Сортировка слиянием является одним из наиболее эффективных методов для односвязных списков и файлов, когда есть лишь последовательный доступ к элементам.

 

 

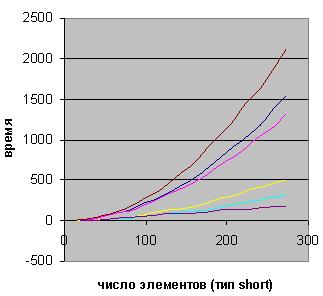
График сравнения скорости работы некоторых алгоритмов:

 

коричневая линия: сортировка пузырьком;

синяя линия: пузырёк модифицированный;

розовая линия: сортировка выбором;

желтая линия: сортировка вставками;

фиолетовая линия: сортировка Шелла.