Представление данных в эвм. Машинная арифметика. Погрешность представления чисел с плавающей точкой и ее влияние на точность вычислений.

 

1)

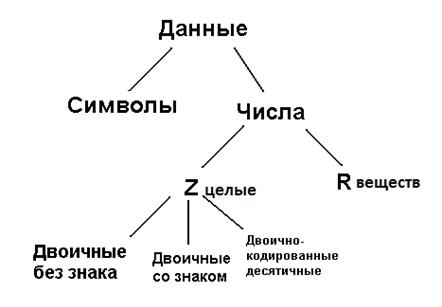
Модель информационных объектов.

 

Х – основание системы исчисления

An-1…. А2 А1 А0 = Аn-1Х^n-1 + Аn-2Х^n-2 + ….. + А0Х⁰ - расширенная запись числа

 

В десятичной системе счисления для записи чисел используются цифры от 0 до 9.Её основанием является число 10. Расширенная запись:

 

Н-р: 2754

2*10^3+7*10^2+5*10^1+4*10^0 = 2754₁₀.

 

В двоичной системе счисления для записи чисел используются только цифры 0 и 1 соответствующие основанию, равному 2. В принятой терминологии их часто называют битами.

 

Н-р:101010₂

 

1*2^5+0*2^4+1*2^3+0*2^2+1*2^1+0*2^0=42₁₀

 

Шестнадцатеричная система счисления:0-9, А=10, B=11, CDEF…

2) Представление целых чисел

Для представления целых чисел в памяти компьютера всегда отводится лишь конечное количество разрядов. Для представления целых чисел в большинстве компьютеров применяются три различных формата, имеющие длину 8, 16 и 32 двоичных разряда соответственно (байтовый формат, формат слова и формат двойного слова).

 

Без знака.

Заносимое в память компьютера число следует представить в двоичной системе счисления и разместить полученную последовательность нулей и единиц по указанному адресу. Если длина двоичной записи оказывается меньше размера выбранного формата, то число следует дополнить нулями слева. Диапазон значений определяется как [0... 2^n - 1], где n есть кол-во разрядов в двоичной записи числа.

 

Количество разрядов	Максимальное число
	2^8-1
	2^16-1
	2^32-1

 

Если полученное в результате вычислений числовое значение превышает допустимый диапазон для выбранного формата, то возникает ситуация переполнения.

 

Выброшенная за пределы разрядной сетки единица не теряется полностью, а сохраняется процессором в специальном битовом регистре, называемым флагом переноса. Но это делается лишь для того, чтобы зафиксировать ситуацию переполнения, а не скорректировать неверный результат операции.

 

Со знаком

С прямым кодом

При знаковом представлении целых чисел возникают такие понятия, как прямой, обратный и дополнительный коды. Представление числа в привычной для человека форме «знак-величина», при которой старший разряд ячейки отводится под знак, остальные k-1 разрядов – под цифры числа, называется прямым кодом. Для положительных чисел используется нулевое значение знакового разряда, для отрицательных он равен единице

Н-р:

Двоичные числа: 1101₂ и 1101₂

В восьмиразрядной ячейке: 00011001 и 10011001

 

Основной недостаток записи и обработки чисел в прямом коде: представление нуля оказывается неоднозначным (+0 и –0). Очевидно, что оба они должны отождествляться процессором с одним и тем же нулевым значением. Другим недостатком прямого кода является то, что операции сложения и вычитания не могут быть выполнены по единой алгоритмической схеме и процессор должен иметь независимые реализации команд для каждой из этих операций. Кроме того, требуется наличие специальной аппаратной логики для анализа знакового разряда.

Прямой код не находит применения в реальных процессорах.

 

В дополнительном коде.

Дополнение числа до основания системы счисления.

Дополнением Xcomp(N) любого n-разрядного числа N до основания Х системы счисления принято называть число

Хсоmр(N) = X^n - N.

 

Н-р: Для трёхзначных десятичных чисел N=625 имеем

Хсоmр(N) = 10^3 – 625=375

 

Однако для представления числового значения X^n уже требуется n+1 знак. Эта проблема может быть легко решена, если исходное соотношение переписать в виде:

Хсоmр(N) = ((X^n - 1) - N) + 1. (выделено неполное доп-е)

Из определения имеем Хсоmр(N) + N = (X^n - N) + N = X^n.

С точностью до потерянной единицы старшего разряда, дополнение числа N до основания системы счисления ведет себя так же, как его отрицание. Если теперь игнорирование единицы переноса из старшего разряда рассматривать как одно из правил выполнения операции сложения, то дополнение числа можно принять за способ представления его отрицания: neg(N) = Xcomp(N)

Исследуем некоторые фундаментальные свойства такой системы.

Заметим, что в системе представления чисел дополнениями до основания системы существует только одно представление нуля.

Где лежит граница между положительными и отрицательными числами при их представлении дополнениями до основания системы счисления?

Деление полного диапазона n-разрядных чисел без знака на три подмножества.

Дополнение до Десятичное

основания число

_______________________________

499 499

… …

001 1

_______________________________

000 0

_______________________________

999 -1

… …

500 -500

Как видно из таблицы, мы получим одно "лишнее" отрицательное значение, для которого не существует равного ему по абсолютной величине положительного числа. Такой результат является платой за единственное представление нуля.

Осталось убедиться в том, что система представления чисел дополнениями до основания системы счисления не требует явного использования операции вычитания, поскольку последняя выражается через операцию сложения как

М-N=M+(-N).

Таким образом, система представления чисел дополнениями до основания системы требует лишь алгоритма получения дополнения. После этого операции сложения и вычитания могут выполняться по единой алгоритмической схеме без проверки знаков и абсолютных значений, необходимых в случае представления в прямом коде. Для получения же дополнения числа до основания системы счисления также можно обойтись без выполнения операции вычитания. Необходимо лишь образовать одноразрядные дополнения его отдельных цифр до X-1 и к результату прибавить единицу.

 

Остановимся на алгоритме получения дополнения для двоичных чисел.

При Х= 2 имеем: 2соmр (N) = 2^n - N = ((2^n - 1) - N) + 1.

((2^n - 1) - N)-дополнение до единицы, обычно обозначается как 1соmр(N)

Предыдущее равенство можно записать в виде: 2соmр (N) = 1соmр(N)+ 1

Алгоритм получения дополнения до двух фактически сводится к нахождению дополнения до единицы. Величина (2^n - 1) представляется единицами во всех n разрядах. Но для любого числа N разность (2^n - 1)- N может быть вычислена простым инвертированием разрядов в его двоичном представлении.

Старший разряд в представлении всякого положительного числа равен нулю, а для отрицательных чисел он установлен в единицу. По аналогии с числами в прямом коде этот разряд обычно называют знаковым разрядом. Однако этот анализ фактически не требуется для реализации операций сложения и вычитания.

 

Пример получения дополнительного кода для 8-разрядных чисел:

 

27₁₀ = 00011011₂

11111111

00011011

11100100

00000001

 

Диапазон допустимых значений целых чисел со знаком в дополнительном коде определяется как -2^(n-1)... + (2^(n-1)-1)

Очевидным признаком переполнения является тот факт, что при сложении двух положительных чисел был получен отрицательный результат. Однако такой критерий не удобен для практического использования, поскольку требует специальной логики анализа знакового разряда, что, в общем-то, не является необходимым для реализации арифметики в дополнительных кодах. Более тонкие наблюдения показывают, что при выполнении сложения возникла единица переноса в старший знаковый разряд, но нет переноса за пределы разрядной сетки. В этом случае принято говорить о несовпадении индексов, или битов, переноса для старшего разряда. При выполнении операции вычитания следовало бы говорить о заеме в старший и из старшего разряда. Легко проверить, что именно факт несовпадения индексов переноса или заема является свидетельством возникшего переполнения по сложению или вычитанию. Контроль этого признака достаточно

прост и вполне естественен, поскольку логика учета переносов всегда присутствует в реализации основных арифметических операций.

 

Система представления целых чисел со знаком в дополнительном коде является одной из наиболее совершенных и используется подавляющим большинством современных микропроцессоров.

 

(Другой алгоритм

1. Модуль числа представить кодом в k двоичных разрядах

2. Значение всех разрядов инвертировать(все нули заменить на единицы, а единицы на нули), получив при этом k разрядный обратный код исходного числа.

3. К полученному обратному коду прибавить единицу)

 

в обратном коде

Здесь за представление всякого отрицательного числа принимается дополнение до единицы 1comp(N) его абсолютной величины N, которое получается простым инвертированием разрядов двоичного представления числа N.

Если диапазон представления положительных чисел ограничить 127₁₀ = 01111111₂, то старший разряд в представлении всякого положительного числа окажется равным нулю, а для отрицательных чисел он будет равен единице. Двоичный шаблон из всех единиц при этом следует считать формальным представлением отрицательного нуля, что говорит о наличие двух нулевых элементов в системе представления чисел в обратном коде. Диапазон допустимых значений от -(2^(n-1)-1) до +(2^(n-1) - 1) для n-разрядных целых чисел.

Реализация арифметических операций сложения и вычитания для чисел в обратных кодах требует закольцовывания старшего и младшего разрядов в представлении числа. Так, например, при реализации сложения единица переноса из старшего разряда должна быть добавлена к младшему биту для получения правильного результата. В этом легко убедиться, складывая, например, некоторое положительное число с не превышающим его

по абсолютной величине отрицательным или два отрицательных числа: правило циклического переноса.

Правила вычитания и обнаружения переполнения являются такими же, как и для чисел в дополнительном коде.

Основным достоинством системы является ее симметричность и простота образования дополнений.

 

00000111₂= 7₁₀

11111100₂ =-3₁₀

00000011₂

00000001₂ единица переноса

00000100₂= 4₁₀

 

Код со смещением.- последний способ представления целых чисел со знаком

В этой системе всякое число N, находящееся в диапазоне от –2^(n-1) до +(2^(n-1)-1), записывается в виде n-разрядного двоичного представления числа N +2^(n-1) которое всегда неотрицательно и имеет значение, меньшее 2^n. Легко видеть, что диапазон чисел, которые могут быть представлены в коде со смещением 2^(n-1), совпадает с диапазоном чисел, представимых с помощью n-разрядных дополнений до двух. Действительно, представление любого числа в обеих системах полностью совпадает, за исключением знаковых разрядов, имеющих всегда противоположные значения. Представление нулевого элемента также является единственным и при выбранном смещении соответствует значению 2^(n-1).

В некоторых специальных случаях, смещение принимается равным 2^(n-1)-1. При этом диапазон от -(2^(n-1)-1) до +2^(n-1).

 

3) Двоично-кодированные десятичные.

В двоично-кодированном десятичном формате BCD десятичные цифры, используемые для записи целых чисел, хранятся в виде 4-битовых двоичных эквивалентов:

0000₂ = 0₁₀

0001 = l

0010 = 2

0011 = 3

0100 = 4

0101 = 5

0110 = 6

0111 = 7

1000 = 8

1001 = 9

Имеются две основные разновидности этого формата: упакованный и неупакованный.

В упакованном BCD-формате всякая цепочка десятичных цифр хранится в виде сплошной последовательности 4-битовых групп.

Н-р: 6253 в виде 0110.0010.0101.0011

В неупакованном BCD-формате каждая цифра находится в младшей тетраде 8-битовой группы, а содержимое старшей тетрады не используется и может быть произвольным.

Н-р: 6253 в виде uuuu0110.uuuu0010.uuuu0101.uuuu0011, где u – игнорируемые разряды.

 

Отрицательные целые числа допускают представление в десятичном прямом или десятичном дополнительном коде.

При выборе десятичного прямого кода для представления знаков плюс и минус могут быть представлены любыми двумя из шести неиспользуемых 4-битовых комбинаций, например 1100 обычно обозначает плюс, а 1101 - минус. Знак допускается размещать до или после цепочки цифр. При использовании неупакованного формата информация о знаке обычно размещается в старшей тетраде младшей или старшей десятичной цифры числа.

Десятичный n-разрядный дополнительный код произвольного целого положительного числа N определяется как 10^n - N. Диапазон от –5*10^(n-1) до +(5*10^(n-1)-1). Десятичный дополнительный код обладает теми же свойствами, что и дополнительный двоичный.

В терминологии IBM неупакованный BCD-формат называют зонным форматом. При этом старшая тетрада в представлении каждой десятичной цифры, кроме младшей, содержит код зоны 1111₂=F₁₆. Старшая же тетрада младшей цифры числа содержит информацию о знаке.

При упаковке зонного формата старшая тетрада младшей цифры сохраняется, а все остальные зонные биты отбрасываются.

 

4)Представление символьной информации

Символьные данные в памяти компьютера представляются числами, записанными чаще всего в формате байта или двухбайтового машинного слова. Кодировочная таблица устанавливает взаимно-однозначное соответствие между элементами множества и числовыми значениями из выбранного диапазона.

 

Для представления символьных данных наибольшее распространение в настоящее время получил Американский стандартный код для обмена информацией ASCII. Изначально

код ASCII использовал лишь семь бит байтового формата, современный вариант кода ASCII уже является 8-разрядным, однако ради унификации и сохранения преемственности с его ранними реализациями полную кодировочную таблицу принято делить на основную и расширенную.

 

Основная таблица ASCII по сути дела соответствует изначальному семибитовому коду с диапазоном значений от 00₁₆ до 7F₁₆. Представленные в ней символы и назначенные им числовые коды полностью стандартизированы и не зависят от типа компьютера и операционной системы. Вторая половина таблицы с кодами от 80₁₆ до FF₁₆ является расширением стандарта ASCII и может, вообще говоря, изменяться на различных вычислительных системах. В этой части таблицы чаще всего размещаются символы национальных алфавитов, математические и др.

Основные коды ASCII включают в себя 95 печатных символов и 33 символа управления.

 

Другой код EBCDIC делит всё множество букв и цифр на группы, или зоны, присваивая каждому из этих символов четыре зонных и четыре цифровых бита.

 

Код стандарт Unicode. Все символы имеют двухбайтовое представление. Использование 16-битного формата позволяет закодировать 65536 символов

5)Представление вещественных чисел

 

В зависимости от способа записи вещественных чисел принято различать их представление с фиксированной и плавающей точкой.

Система представления с фиксированной точкой предполагает, что положение десятичной точки, разделяющей целую и дробную части вещественного числа, фиксировано из каких-либо соображений, чаще всего подсказанных характером обрабатываемых числовых данных. Так, мы можем договориться, что будем записывать вещественные числа в виде последовательности n десятичных цифр, фиксируя положение десятичной точки таким образом, чтобы в дробной части числа всегда было m знаков. Тогда в целой части числа будем иметь не более k = n - m десятичных цифр.

d_k-1…d₁d₀.d_-1d_-2…d_-(m-1)d_-m

Очевидное неудобство такого способа представления связано с явной ограниченностью диапазона при небольшом количестве позиций, отводимых для записи числа.

(Число с фиксированной точкой – формат представления вещественного числа в памяти ЭВМ в виде целого числа. При этом само число х и его целочисленное представление хꞋ связаны формулой: х=хꞋ*z, где z – цена(вес) младшего разряда. Если z<1 то, чтобы целые числа кодировались без погрешности выбирают целое число u(машинную единицу) и z=1\u). z>1, его делают целым.)

 

Способ представления вещественных чисел в формате с плавающей точкой предполагает, что величина всякого числа F определяется как F=m*X^k где Х есть основание системы счисления, а величины m и k называются соответственно мантиссой и порядком. X обычно равно 10, а для внутренних машинных форматов всегда принимается равным 2. Значения мантиссы и порядка при этом также представляются в двоичной системе счисления. Формат плавающей точки опирается на нормализованную форму записи числа.

 

Нормализованная форма числа.

Нормализованная запись отличного от нуля вещественного числа – это запись вида F=±m*X^k, где k – целое число, а m – правильная X-ичная дробь, у которой первая цифра после запятой не равна нулю, т.е. 1\P≤m≤1.

 

Примеры нормализации чисел:

а) 0=0,0 × 10⁰ (возможная нормализация нуля)

б) 3,14=0,314 × 10¹ (количество значащих цифр не изменилось)

в) 1000=0,1 × 10⁴ (количество значащих цифр уменьшилось с 4 до 1)

г) 0,0000107₈=0,107₈ × 8^-4 (количество значащих цифр уменьшилось с 7 до 3)

д) 1000,0001₂=0,10000001₂ × 2⁴ (количество значащих цифр уменьшить невозможно)

 

Нормализованное число (формата IEEE – Института инженеров по электронике и электротехнике):

F=(-1)^S 1.f₁…f_n * 2^k

где через s обозначен знаковый разряд, f_i есть ноль или единица дробной части двоичного представления мантиссы, a k определяет двоичный порядок числа.

 

Любые операции над ненормализованными операндами считаются недопустимыми. Единица целой части мантиссы не заносится в память компьютера, но принимается во внимание при выполнении арифметических операций. Принято говорить, что она является скрытым разрядом мантиссы.

Двоичный порядок k представляют в коде со смещением. Положительный порядок будет содержать единицу в старшем разряде, а для отрицательных значений порядка этот разряд равен нулю. Легко проверить, что если в памяти компьютера поле порядка в коде со смещением будет непосредственно следовать за полем мантиссы, то сравнение двух вещественных чисел может быть выполнено путем сравнения двух целых чисел без знака, полученных формальным объединением двоичных разрядов мантиссы и порядка.

 

В соответствии со стандартом IEEE для внутреннего машинного представления вещественных чисел используется короткий (32 бита) и длинный (64 бита) форматы, а также временный (80 бит). Их также часто называют с одинарной и удвоенной точностью.

 

Формат Мантисса Порядок Знак Диапазон

 

Короткий биты 0... 22 биты 23..30 бит 31

(32 бита) 23 (+1) база=127 10^-38<|x|<10^38

 

Длинный биты 0... 51 биты 52.. 62 бит 63

(64 бита) 52 (+1) база = 1023 10^-308<|x|<10^308

 

 

Снижение точности машинного представления вызывается операциями над числами очень разного порядка, а также вычитанием близких чисел.

6) Модуль разности между значением числа х и некоторым его представлением хꞋ называется абсолютной погрешностью представления х.

Относительной погрешностью представления х называют величину |(х-хꞋ)\х|.

Абсолютная погрешность говорит о том, на сколько полученный результат отличается от истинного результата. Относительная погрешность показывает, сколько верных старших значащих цифр содержит результат

 

Плавающая точка.

 

sk

sm

bq

…

b1

a1

an

 

Первые два разряда служат для представления знаков порядка (s_k) и мантиссы (s_m). Следующие q разрядов используются для представления абсолютной величины порядка числа (k), а остальные n разрядов – для представления абсолютной величины матиссы. В каждом разряде ячейки может храниться одно из двух значений: 0 и 1.

Билет №6

Базовые элементы архитектуры микропроцессоров. Управление потоком команд. Базирование и индексирование памяти. Управление стеком. Битовые флаги состояния и управления. Организация памяти и формирование исполнительного адреса на примере реального режима микропроцессоров Intel x86.

 

1) Под термином микропроцессор будем понимать некоторое однокристальное полупроводниковое устройство, объединяющее в одной микросхеме способность выполнять арифметико-логические операции, управлять выборкой команд и данных из оперативной памяти и осуществлять обмен с внешними устройствами через их интерфейсы. Далее термины процессор и микропроцессор будут тождественные. Будет предполагать, что наш абстрактный процессор ориентирован только на обработку целочисленных данных и не содержит команд и характерных элементов архитектуры для выполнения операций над вещественными числами.

 

Блочная схема процессора.

Элементы, играющие пассивную роль, лежат в левой части схемы. Элементы, играющие активную роль, справа.

 

1. Регистр общего назначения (General Purpose Registers) – основные программно доступные элементы архитектуры микропроцессора.

Временное сохранение данных при выполнении команд программы (под данными понимаются данные и адреса). Идейно, можно разделить РОН на Регистры данных и Регистры адресов.

Регистры данных являются локальной памятью процессора, в которой могут размещаться аргументы и результаты выполнения машинных команд. Адресные регистры служат для задания адресов операндов в аргументах машинных команд и необходимы для гибкой адресации основной памяти. Их содержимое указывает на ячейку, из которой нужно прочесть или в которую следует записать некоторый элемент данных. Поэтому адресные регистры иногда называют указателями.

Управление потоком команд.

 

2. Счётчик команд (Указатель команд)

 

Указатель команд (Instruction Pointer)à хранит адрес следующей команды.

Последовательность действий при выборе команды:

1) Выборка команды из ОП или очереди команд по текущему значению IP

2) Декодирование команд

3) Изменение значений IP

4) Опрос подсистемы прерываний (например, нажатие клавиш клавиатуры при выполнении команды вызывает прерывание команды, для выполнения действия клавиши)

5) Выполнение команды

 

Выполняем команды по А, пока не встретили вызов некоторой операции В. Переходим в В, выполняем, возвращаемся в А и продолжаем выполнение в указанном порядке. Но как понять, на какой адрес вернуться после выполнения В? Этот адрес сохранен в IP, и сохраняет до момента нашего возвращения.

 

3. Регистр состояния (иногда, «регистр флагов») –

Фиксирует внутренние изменения состояния процессора и результаты выполнения команд. Но результат выполнения команд здесь нужно понимать, как микро результаты выполнения микро задач (0 или не 0, например).

 

4. Регистры управления памятью – некоторые регистры, обслуживающие процессы конвертации и преобразования адресов из одной системы в другую.

Используются устройством управления памятью, для преобразования адресов.

 

5. Арифметико-логическое устройство – выполняет все действия, вычисления процесса, инициированные нашей программой.

Реализует операции, предусмотренные машинными командами, но не интересуется, зачем это делалось – выполняет команды Управляющего устройства.

 

6. Устройство управления – логический модуль процесса, «говорящие» АЛУ, что конкретно ему необходимо делать.

Устройство управления (Control Unit)

1) Выборка команд

2) Расшифровка кода операции

3) Декодирование и извлечение операндов

4) Передача или загрузка операндов в АЛУ

5) Управление работой АЛУ

 

7. Устройство управления памятью

(Memory Management Unit)

1) Преобразование адресов

2) Реализация механизмов защиты памяти

3) Разделение адресного пространства задач и операционной системы

(абстрактная картинка)

 

Для повышения эффективности управления памятью, как логическое, так и физическое адресные пространства делятся на разделы фиксированного или переменного размера. Логические разделы фиксированного размера принято называть страницами, а равные им по величине разделы физической памяти – блоками. Разделы переменного размера обычно называют сегментами.

 

8. Устройство управления шиной – логические элементы, планирующие загрузку магистрали. Логика управления шиной обеспечивает физический интерфейс процессора со всеми остальными устройствами, подключенными к системной шине.

(Bus Control Unit)

1) Синхронизация работы на системной шине

2) Буферирование данных

3) Разрешения возможных конфликтов на системной шине

 

9. Очередь команд (Instruction Queue)

Временное хранение команд перед их передачей на выполнение.

 

10. КЭШ данных (Data Cache)

Сохранение часто используемых данных

 

11. КЭШ команд (Instruction Cache)

Сохранение часто используемых команд

 

2)Базирование и индексирование памяти.

Простейшими структурами данных, работа с которыми поддерживается непосредственно аппаратурой процессора, являются однородные линейные массивы и стеки.

 

Однородный линейный массив представляет собой последовательность элементов данных одной и той же длины, к каждому из которых возможен непосредственный доступ с помощью целочисленного индекса, указывающего позицию элемента в последовательности.

 

Адресация элементов массива:

 

адрес начала массива
a0	a1		ak		an
смещение k-ого элемента

Адрес начала размещения массива в памяти обычно считается известным, а однородность его элементов делает доступ к ним простым и эффективным. Если обозначить через А₀ обозначить адрес начала массива, то для адреса k-ого элемента имеем:

Ак=Ао+k*sizeof(E), где k порядковый номер, или индекс, sizeof(E) определяет размер элемента Е в байтах.

 

Логической и аппаратной основой для доступа к элементам массива являются принципы базирования и индексирования.

 

 

Базирование массива:

 

Аmax 0 1 АБСОЛЮТНЫЙ АДРЕС
			а0	а1		ак
база массива	смещение ак

Базирование означает простой перенос начала отсчёта адресов памяти на первый элемент массива, как это показано на рисунке. Новое начала отсчёта принято называть базой или базовым адресом массива.

Смещение или индекс элемента выражает его расстояние в байтах от выбранной базы.

 

Аналогично базированию, для хранения и модификации индексов могут быть использованы либо произвольные рабочие или адресные регистры, либо специально зарезервированные для этой цели регистры индекса.

Стек является частным случаем однородного линейного массива переменного размера со специальной дисциплиной доступа к его элементам.

3) Управление стеком.

 

Есть два вида структурных данных, работа с которыми поддерживается непосредственно процессором. Это линейный массив и стек. С массивом все понятно, стек рассмотрим подробнее.

 

Стек (англ. stack — стопка) — динамическая структура данных с методом доступа к элементам LIFO(Last In — First Out, последним пришел — первым вышел). Чаше всего принцип работы стека сравнивают со стопкой тарелок: чтобы взять вторую сверху, нужно взять верхнюю.

 

Для стека включение и исключение элементов ограничено лишь одним концом, вершиной стека. Текущее положение вершины определяется значением в специальном адресном регистре, называемом указателем стека. Этот регистр зарезервирован для работы со стеком и обычно не может быть использован ни для каких иных целей.

 

Добавление элемента, называемое также проталкиванием (push), возможно только в вершину стека (добавленный элемент становится первым сверху), выталкивание (pop) — также только из вершины стека, при этом второй сверху элемент становится верхним.

 

Особенности реализации стека. Стек обычно реализуется на базе однородного линейно-упорядоченного массива фиксированного размера, называемого вектором. Фиксированный размер вектора определяет глубину стека, то есть то максимальное количество элементов, которое можно поместить в него многократным обращением к команде push, не выполнив при этом не одной команды pop.

 

Стек широко используется в программировании на низком уровне (то есть, как правило, на языке ассемблера) и является неотъемлемой частью архитектуры современных процессоров. Компиляторы языков программирования высокого уровня используют стек для передачи параметров при вызове подпрограмм, процессоры — для хранения адреса возврата из подпрограмм.(Часто будет использоваться позднее, запоминаем…)

 

4) Флаги:

 

Флаг – это некоторый двоичный разряд, который служит для проверки состояния чего нибудь. Например нам надо узнать а>б или нет? Операции сравнения в принципе нет, поэтому мы можем посчитать (а - б), если больше нуля (основываясь на двоичном представлении), то ставим флаг 1, если нет, то 0. Флаги отражают состояние программы. Флаги делятся на две группы: состояния и управления. Флаг управления – например, флаг маскирования прерывания, т е невосприимчивость программы в данный момент к прерываниям.

Флаги состояния, или условий, отражают результат завершения предыдущей операции по большей части используются командами условной передачи управления для организации разветвлений в программе.

Флаг переноса CF используется для фиксации единицы переноса из старшего разряда результата при выполнении арифметических операций или команд сдвига. Равен 1, если перенос разряда за пределы разрядной сетки. В противном случае равен 0.

Флаг паритета, или флаг четности. Дополняет до нечётного количества единиц в младшем байте результата выполнения предыдущей машинной команды. Его роль состоит в обеспечении контроля над правильностью работы процессора и подсистемы памяти.

Флаг нуля ZF устанавливается в единицу при получении нулевого результата и сбрасывается в ноль, если результат арифметической или логической операции отличен от нуля. Флаг нулевого результата – равен 1, если результат выполнения команды равен нулю. В противном случае равен 0.

Флаг знака SF. Его значение совпадает со старшим битом результата. Флаг SF показывает знак результата предыдущей операции. Флаг знака – равен 1, если результат выполнения команды меньше нуля. И равен 0, если результат больше нуля.

Флаг переполнения OF устанавливается в единицу, если результат выполнения операции над числами со знаком, представленными в дополнительном коде, находится вне допустимого диапазона. Флаг переполнения – равен 1, если возникло переполнение в команде обработки целых чисел со знаком.

Флаги управления оказывают влияние на выполнение некоторых специальных функций и операций. Флаг управления – например, флаг маскирования прерывания, т е невосприимчивость программы в данный момент к прерываниям.

 

5) Сегментная организация памяти.

В основе сегментной модели лежит фундаментальное понятие сегмента. Под сегментом следует понимать область в адресном пространстве оперативной памяти. Размер этой области не фиксирован конструкцией микропроцессора, но ограничен сверху разрядностью его адресных регистров. Положение сегмента в адресном пространстве в общем случае может быть произвольным и фиксируется заданием сегментной базы. Использование сегментов позволяет перейти от абсолютной к относительной адресации элементов данных в оперативной памяти. Здесь под абсолютной адресацией понимается отсчёт адресов от начала адресного пространства, а относительный адрес представляет собой смещение элемента данных от начала сегмента.

 

В случае сегментной организации памяти логическое адресное пространство представляется состоящим из наборов блоков или сегментов разного размера. Размер сегмента может меняться динамически (например, сегмент стека) и ограничен лишь разрядностью процессора (при 32-разрядной адресации это 2³² байт или 4 Гбайт). В элементе таблицы сегментов помимо физического адреса начала сегмента обычно содержится и длина сегмента. Если размер смещения в виртуальном адресе выходит за пределы размера сегмента, возникает исключительная ситуация. Логический адрес – упорядоченная пара v=(s,d), номер сегмента и смещение внутри сегмента. В системах, где сегменты поддерживаются аппаратно, эти параметры обычно хранятся в таблице дескрипторов сегментов, а программа обращается к этим дескрипторам по номерам-селекторам. При этом в контекст каждого процесса входит набор сегментных регистров, содержащих селекторы текущих сегментов кода, стека, данных и т. д. и определяющих, какие сегменты будут использоваться при разных видах обращений к памяти. Это позволяет процессору уже на аппаратном уровне определять допустимость обращений к памяти, упрощая реализацию защиты информации от повреждения и несанкционированного доступа. Физический адрес формируется путем прибавления смещения к адресу начала сегмента.

 

Недостаток сегментной организации памяти: абсолютный адрес элемента данных не может быть задан однозначно в виде пары Сегмент:Смещение. Это происходит потому, что сегменты являются не физическими, а скорее логическими структурными единицами.

 

6) Микропроцессор Intel x86

 

В 1976 году появился первый микропроцессор линейки 80x86 – 8086, 16-битный процессор на одной микросхеме. За ним был создан 8088, он отличался тем, что работал на 8-ми битной шине, а из-за распространенности в те времена 8-ми битной периферии компьютеры на его базе стоили дешевле. Ни 8086, ни 8088 не умели обращаться более, чем к 1 мегабайт памяти. К началу 80-х это стало серьезной проблемой, поэтому Intel выпустила модель 80286, которая была совместима с 8086. Основной набор команд остался фактически тем же, однако память была устроена немного по-другому. Следующим шагом был 32-х битный процессор 80386, выпущенный в 1985 году. Он так же был совместим со всеми старыми версиями. Некоторые его блоки в некоторых ситуациях могли функционировать параллельно. Наряду с очевидными плюсами совместимости были и минусы, такие как необходимость использования старой архитектуры, обремененной старыми ошибками. Спустя 4 года появился 486-ой. Он был еще быстрее, имел 8 килобайт кэш-памяти и умел выполнять операции с плавающей точкой. Также новый процессор содержал встроенные средства поддержки многопроцессорного режима и конвейер из пяти блоков. Первый блок – блок выборки команд, 2-ой – блок декодирования, 3-ий – блок выборки операндов, 4-ой – выполнение команды, наконец 5-ый - блок возврата. Идея состоит в следующем: во время цикла 1