
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Влияние основания системы счисления на диапазон представления чисел в эвм и информационных системахСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Диапазон представляемых чисел зависит от основания характеристики и числа разрядов, выделенных для изображения порядка. Использование плавающей запятой значительно расширяет диапазон представляемых чисел в машине. Однако недостатком машин с плавающей запятой является увеличение времени выполнения арифметических операций в связи с необходимостью оперировать не только с мантиссами, но и с порядками чисел, а также осуществлять их нормализацию. К тому же это приводит к усложнению схем машины. В современных машинах, как правило, используются обе формы представления чисел, что позволяет учитывать особенности решаемых задач и тем самым повысить общую скорость вычислений. При этом у одинаковых по длине форматов чисел с плавающей точкой с увеличением основания системы счисления существенно расширяется диапазон представляемых чисел. Достоинством использования шестнадцатеричной системы для представления чисел с плавающей запятой (точкой) является возможность увеличения диапазона представляемых чисел в машине. 8. Особенности выполнения арифметических операций в 2-й системе счисления. Включает часть ответов из 9,10. Брать из них вычисления ОК, ПК, ДК (+,- числа,0). Кодирование двоичных чисел при выполнении арифметических операций. ПК и ОК. Выполнение в них алгебраического сложения чисел. Для представления знаковых целых чисел используются три способа: 1) прямой код; 2) обратный код; 3) дополнительный код. Все три способа используют самый левый (старший) разряд битового набора длины k для кодирования знака числа: знак “плюс” кодируется нулем, а “минус” — единицей. Остальные k-1 разрядов (называемые мантиссой или цифровой частью) спользуются для представления абсолютной величины числа. N1+N2=N3 1)N1>0,N2>0 2)N1>0,N2<0 3)N1<0,N2>0 4)N1<0,N2<0 0«+» 1 «-»
ПК
Арифм.опер. необходимо различать операции над числами и над знаками.
ОК
Отр.число в ОК необход. в знак разряд поставить 1, а в числовых 0->1 и 1->0
0 в коде. В ДК знак в 0 не различается
Сложение в ПК (прямом коде) не используется т.к. N1+N2=N3. Арифметическое сложение кодируемых чисел в ОК: 1. N1>0, N2>0 – обычное сложении 2. N1>0, N2<0; |N1|>|N2| N3ок = N1 + (2 - N2 - 2-n) = 2 + (N1 - N2) - 2-n = 2 + N3 - 2-n Пример: N1 = +0,10112 = 11/1610 N2 = - 0,01012 = -5/16 N1ок = 0,1011 N2ок = 1,1010
+1 N3 = 0,0110 = 6/16 3. N1<0, N2>0 N3ок = 2 – N3 – 2-n – 2-n = N3ок - 2-n 4. N1<0, N2<0 Пример: N1 = - 0,01112 = -7/1610 N2 = - 0,01012 = -5/16 N1ок = 1,1000 N2ок = 1,1010
+1 N3 = - 0,1100 = -12/16 Дополнительный код. Выполнение алгебраического сложения чисел.
Для представления знаковых целых чисел используются три способа: 1) прямой код; 2) обратный код; 3) дополнительный код.
Все три способа используют самый левый (старший) разряд битового набора длины k для кодирования знака числа: знак “плюс” кодируется нулем, а “минус” — единицей. Остальные k-1 разрядов (называемые мантиссой или цифровой частью) спользуются для представления абсолютной величины числа.
Отриц. число в ДК в знак 1, в числовых заменить 0->1 1->0 кроме последнего.
ДК: 2.N1>0, N2<0; |N1|>|N2| N3дк = N1 + 2 - N2 = 2 + (N1 - N2) = 2 + N3 Пример: N1 = +0,01112 = 7/1610 N2 = - 0,01012 = -5/16 N1дк = 0,0111 N2дк = 1,1011 N3ок = N3 = 0,0010 = 2/16 4.N1<0, N2<0 N3дк = 2 - N1 + 2 - N2 = 2 + (N1 - N2) + 2 = 2 - N3 + 2 = - N3дк + 2 Пример: N1 = - 0,01112 = -7/1610 N2 = - 0,01012 = -5/16 N1ок = 1,1001 N2ок = 1,1011 N3ок = N3 = - 0,1100 = -12/16
Выводы: 1. При суммировании операндов в ДК результат тоже получается в ДК. 2. Суммирование операндов в ДК занимает меньше времени. Поэтому ДК – основной код во всех современных ВМ, а также потому, что -0 представляется в нем как 0. Хранение операндов в памяти происходит тоже в ДК. Сложение двоичных чисел, представленных в форме с плавающей запятой. Алгебраическое сложение кодированных чисел Для выполнения алгебраического кодирования ПК не используется, в нем разделяются операции над знаками и над модулями чисел. ОК: N1+N2=N3 1. N1>0, N2<0; | N1|>| N2|, N1 +N2 =N3>0 N1ОК+ N2ОК= N1+10- N2-10-n=10+(N1 -N1)-10-n=10+N3-10-n N1=+0,1011=+ N2=-0,0110=- N3OK=10,0100 N3OK=0,0101=+ 2. N1>0, N2<0; | N1|<| N2|, N1 +N2 =N3<0 N1ОК+ N2ОК= N1+10- N2-10-n=10+(N1 -N1)-10-n=10-N3-10-n=-N3OK N1=+0,0111=+ N2=-0,1101=- N3OK=1,1001 N3OK=-0,0110=- 3. N1<0, N2<0; N1ОК+ N2ОК=10- N1-10-n +10-N2-10-n=10+(-N1 -N1)-10-n+10-10n=10-N3-10-n N1=-0,0100=- N2=-0,1001=- N3OK=11,0001 N3OK=1,0011-N3=-0,1101=- При выполнении сложения в ОК результат получается тоже в ОК. При выполнении переноса из знакового разряда, эта 1 по цепи циклического переноса добавляется к младшему разряду. ДК: 1. N1>0, N2<0; | N1|>| N2|, N1 +N2 =N3>0 N1ДК+ N2ДК= N1+10- N2 =10+(N1 -N1) =10+N3 N1=+0,1011=+ N2=-0,1000=- N3ДK=10,0011 N3=+ 2. N1>0, N2<0; | N1|<| N2|, N1 +N2 =N3<0 N1ДК+ N2ДК= N1+10- N2=10+(N1 -N1)=10-N3=N3ДK N1=+0,0011=+ N2=-0,1100=- N3ДK=1,0111 N3ДK=-0,1001=-
3. N1<0, N2<0; N1+N2=N3<0 N1ДК+ N2ДК=10-N1+10-N2 =10+(-N1 -N1)-10=10-N3ДК N1=-0,0111=- N2=-0,1000=- N3ДK=11,0001 N3=-0,1111=- При выполнении сложения в ДК, результат тоже получается в ДК. При выполнении переноса из знакового разряда, эта 1 теряется. Время выполнения по отношению с ОК меньше, т.к. отсутствует цикл переноса.
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 439; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.78.242 (0.007 с.) |









 N3ок = 10,0101
N3ок = 10,0101




 N1OK=0,1011
N1OK=0,1011 N2OK=1,1001
N2OK=1,1001
 N1OK=0,0111
N1OK=0,0111 N2OK=1,0010
N2OK=1,0010 N1OK=1,1011
N1OK=1,1011 N2OK=1,0110
N2OK=1,0110 N2ДK=1,1000
N2ДK=1,1000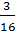
 N2ДK=1,0100
N2ДK=1,0100



