
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вектор временной развертки, обобщенной временной разверткиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Один из самых простых способов введения системы координат связан с простым перечислением всех операций, т.е. с линейным упорядочением вершин графа алгоритма. При сохранении уровня достоверности результатов самой важной характеристикой процесса реализации алгоритма является время его выполнения. Если алгоритм реализуется каким-либо образом на какой-нибудь реальной или гипотетической, последоватьельной или параллельной вычислительной системе, то тем самым определяются моменты выполнения всех операций этого алгоритма. Перенумеруем вершины графа алгоритма любым способом и обозначим через Сам по себе вектор Если при рассмотрении вектора Если из Время Рассмотрим временные ограничения, возникающие в процессе ввода-вывода информации. Обозначим через Пусть фиксирован алгоритм и определен его граф. Обозначим через Если определены какие-то ограничения на параметры вычислительных систем, то тем самым определяется во множестве Время реализации алгоритма Одной из важнейших характеристик, определяющих эффективность алгоритма, является время его реализации на вычислительной системе. Конечно, это время зависит не только от алгоритма, но и от структуры и временных характеристик вычислительной системы. Алгоритмы, считавшиеся эффективными на однопроцессорных ЭВМ, нередко становятся очень неэффективными на многопроцессорных системах. Как оценивать время реализации алгоритма? Очевидно, что прямое его измерение на конкретной ЭВМ дает возможность сравнивавть временные характеристики различных алгоритмов только по отношению к данной ЭВМ. По отношению к другой ЭВМ аналогичное сравнение, вообще говоря, дает другие результаты. Поэтому необходимо абстрагироваться от вычислительной системы. Для однопроцессорных ЭВМ это происходит за счет сравнения количества арифметических операций. Формально можно считать, что число операций – это время реализации алгоритма на абстрактной однопроцессорной машине, у которой время реализации любой операции равно 1, а время выполнения всех других процедур (ввод-вывод данных, взаимодействие с памятью, передача данных по каналам связи и т.п.) равно 0. При этом предполагается, что операции выполняются подряд без какого-либо простоя в работе ЭВМ. Как было показано на примерах, сравнение времен реализации алгоритмов по числу операций становится неприемлемым, если реализацию алгоритмов проводить на параллельных вычислительных системах. Поэтому и абстрактная последовательная ЭВМ, используемая для сравнения времен реализации алгоритмов, также оказыванется неприемлемой для этой цели. Теперь в качестве подходящей модельной вычислительной системы выступает граф-машина. Есть одно принципиальное отличие между абстрактной последовательной ЭВМ и граф-машиной. Именно, на первой реализуются все алгоритимы, на второй – только один. Будем исследовать множество временных разверток
Вопросы 1. Можно ли любой ориентированный ациклический граф считать графом некоторого алгоритма? Почему? 2. Как должны соотносится между собой время работы алгоритма и время, которое затрачивается на его анализ? 3. В чем состоит основная проблема анализа алгоритмов при помощи соответствующих им графов? 4. Что представляет из себя вектор обобщенной временной развертки, чем он отличается от вектора временной развертки? 5. Что такое вектор реализации алгоритма? Когда вектор реализации нулевой? 6. Как временная развертка определяет время появления и время существования информации? 7. Как определяется время задержки информации на дуге? Определение вектора задержек. 8. Какие временные ограничения возникают в процессе ввода-вывода информации? Как формируется вектор начальных условий? 9. Как связаны между собой 10. От чего зависит время реализации алгоритма на вычислительной системе? 11. Есть ли прямая связь между эффективностью алгоритма на однопроцессорных ЭВМ и многопроцессорных системах? Пояснить.
Литература 1. Воеводин В.В. Параллельные вычисления / В.В.Воеводин, Вл.В.Воеводин. — СПб.: БХВ-Петербург, 2002. — 608 с. 2. Харари Ф. Теория графов / Ф.Харари; пер.с англ. В.П.Козырева. — М.: Мир, 1973. — 300 с. 3. Уилсон Р. Введение в теорию графов / Р.Уилсон. — М.: Мир, 1977. — 207 с. 4. Кристофидес Н. Теория графов. Алгоритмический подход / Н.Кристофидес. — М.: Мир, 1978. — 432 с. 5. Новиков Ф.А. Дискретная математика для программистов / Ф.А.Новиков. — СПб.: Питер, 2006. — 364 с. 6. Иванов Б.Н. Дискретная математика. Алгоритмы и программы / Б.Н.Иванов. — М.: Лаборатория Базовых Знаний, 2001. — 288с.
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 745; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 время окончания процесса реализации операции, соответствующего і -ой вершине. Таким образом, с каждой реальной или гипотетической реализацией алгоритма можно связать вектор
время окончания процесса реализации операции, соответствующего і -ой вершине. Таким образом, с каждой реальной или гипотетической реализацией алгоритма можно связать вектор  , который показывает, как протекает процесс реализации во времени.
, который показывает, как протекает процесс реализации во времени. не содержит никакой информации о характеристиках используемой вычислительной системы. Поэтому, если при этом координаты вектора
не содержит никакой информации о характеристиках используемой вычислительной системы. Поэтому, если при этом координаты вектора  , необходимое для реализации
, необходимое для реализации  ой операции. Если из
ой операции. Если из  ой вершины графа алгоритма идет дуга в
ой вершины графа алгоритма идет дуга в  . Поэтому параметр
. Поэтому параметр  будем называть вектором реализации. Для обобщенных временных разверток
будем называть вектором реализации. Для обобщенных временных разверток  .
. эта информация начинает использоваться устройством, относящимся к
эта информация начинает использоваться устройством, относящимся к  и
и  время задержки информации на дуге, связывающей
время задержки информации на дуге, связывающей  . Неотрицательный вектор
. Неотрицательный вектор 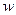 с координатами
с координатами  будем называть вектором задержек.
будем называть вектором задержек. вектор, координатами которого являются координаты вектора развертки
вектор, координатами которого являются координаты вектора развертки 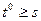 , где
, где 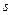 - заданный вектор, неравенство между векторами означает систему неравенств между соответствующими их координатами. Это говорит о том, что исследуются временные характеристики процессов реализации алгоритмов при условии, что заданы ограничения на моменты ввода информации. Вектор
- заданный вектор, неравенство между векторами означает систему неравенств между соответствующими их координатами. Это говорит о том, что исследуются временные характеристики процессов реализации алгоритмов при условии, что заданы ограничения на моменты ввода информации. Вектор  множество всех обощенных временных разверток для этого алгоритма. Через
множество всех обощенных временных разверток для этого алгоритма. Через  обозначим множество всех существующих и не существующих, реальных и гипотетических вычислительных систем, на которых алгоритм может быть реализован. Ясно, что любая конкретная ЭВМ входит во множество
обозначим множество всех существующих и не существующих, реальных и гипотетических вычислительных систем, на которых алгоритм может быть реализован. Ясно, что любая конкретная ЭВМ входит во множество  или
или  или
или 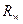 . В свою очередь в подмножествах
. В свою очередь в подмножествах  , а также
, а также  для некоторого вектора
для некоторого вектора  , выбираемого по вектору
, выбираемого по вектору  определяет совокупность обобщенных временных разверток. Задание вектора реализации
определяет совокупность обобщенных временных разверток. Задание вектора реализации 


