Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие внутреннего параллелизма алгоритма и его использованиеСодержание книги
Поиск на нашем сайте В процессе длительного использования последовательных компьютеров был накоплен и тщательно отработан огромный багаж численных алгоритмов и программ. Появление параллельных компьютеров вроде бы должно было привести к массовому созданию новых методов. Но этого не произошло [Воеводин]. Попытка разработать специальные параллельные методы, в частности, методы малой высоты, оказалась на практике несостоятельной. Как использовать старый алгоритмический и программный багаж на параллельных компьютерах? Возьмем любой алгоритм, записанный в виде математических соотношений, последовательных программ или каким-либо иным способом. Допустим, что по этой записи для него удалось построить граф алгоритма. Предположим, что для этого графа обнаружена параллельная форма с достаточной шириной ярусов. Тогда рассматриваемый алгоритм принципиально можно реализовать на параллельном компьютере. Очень важно, что параллельная реализация алгоритма будет иметь такие же вычислительные свойства, как и любая другая [Воеводин]. В частности, если исходный алгоритм был численно устойчив, то он останется таким и в параллельной форме. Подобный параллелизм в алгоритмах называется внутренним. В старых, давно используемых и хорошо отработанных алгоритмах довольно часто удается обнаружить хороший запас внутреннего параллелизма. Использование внутреннего параллелизма имеет · достоинство: не нужно тратить дополнительные усилия на изучение вычислительных свойств вновь создаваемых алгоритмов; · недостатки: необходимость определять и исследовать графы алгоритмов. В тех случаях, когда внутреннего параллелизма какого-либо алгоритма недостаточно для эффективного использования конкретного параллельного компьютера, приходится заменять его другим алгоритмом, имеющим лучшие свойства параллелизма. Для многих задач разработано большое количество различных алгоритмов, поэтому выбрать подходящий алгоритм почти всегда удается. Однако осуществить этот выбор не легко, т.к. нужно знать параллельную структуру алгоритмов. В силу этого чрезвычайно актуальными являются сведения о параллельных свойствах алгоритмов, а также знания, позволяющие эти сведения получать. Пример. Необходимо вычислить произведение
где
Формула (25) не определяет алгоритм вычисления элементов матрицы Допустим, что выбран следующий алгоритм реализации (25):
Построим граф алгорима (35). Будем считать, что вершины графа соответствуют операциям вида Граф алгоритма распадается на Этот пример хорошо иллюстрирует, насколько важно правильно выбрать расположение вершин графа алгоритма. Если, например, расположить вершины на прямой без какой-либо связи с индексами
Рис. 12.1
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1131; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.005 с.) |

 ,
, -
- 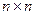 -матрицы с элементами
-матрицы с элементами  соответственно. Элементы матрицы
соответственно. Элементы матрицы 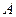 будем обозначать
будем обозначать  :
: . (25)
. (25) . Отсутствие указания о соблюдении какого-либо порядка перебора индексов
. Отсутствие указания о соблюдении какого-либо порядка перебора индексов  говорит о возможном параллелизме вычислений.
говорит о возможном параллелизме вычислений. (35)
(35) . При построении графа не будем сначала показывать вершины и инцидентные им дуги, связанные с вводом элементов матриц
. При построении графа не будем сначала показывать вершины и инцидентные им дуги, связанные с вводом элементов матриц  Чтобы не вносить в исследование графа алгоритма дополнительные трудности, вершины графа нельзя располагать произвольно. Рассмотрим прямоугольную решетку в трехмерном пространстве с координатами
Чтобы не вносить в исследование графа алгоритма дополнительные трудности, вершины графа нельзя располагать произвольно. Рассмотрим прямоугольную решетку в трехмерном пространстве с координатами  . Во все целочисленные узлы решетки для
. Во все целочисленные узлы решетки для  поместим вершины графа. Анализируя (35), видно, что в вершину с координатами
поместим вершины графа. Анализируя (35), видно, что в вершину с координатами  будет передаваться результат выполнения операции, соответствующей вершине с координатами
будет передаваться результат выполнения операции, соответствующей вершине с координатами  .
. не связанных между собой подграфов. Каждый подграф содержит
не связанных между собой подграфов. Каждый подграф содержит  вершин и представляет один путь, расположенный параллельно оси
вершин и представляет один путь, расположенный параллельно оси 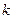 . Для
. Для  граф алгоритма представлен на рис. 12.1(а). В полном графе имеется множественная рассылка данных. Элемент
граф алгоритма представлен на рис. 12.1(а). В полном графе имеется множественная рассылка данных. Элемент  рассылается по всем вершинам, имеющим те же самые значения координат
рассылается по всем вершинам, имеющим те же самые значения координат  . Элемент
. Элемент  рассылается по всем вершинам, имеющим те же самые координаты
рассылается по всем вершинам, имеющим те же самые координаты  . Для
. Для