Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование непрерывной системы.
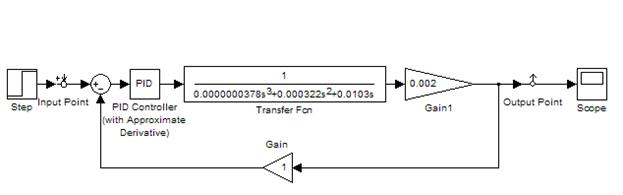
Проведём моделирование системы автоматического управления средствами программного пакета MATLAB (рис.12). Воспользуемся расширением данного программного продукта – средой моделирования Simulink [1].
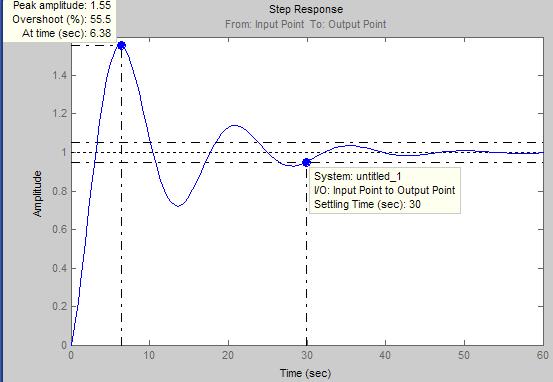
Рис. 12. Модель системы автоматического управления в среде Simulink Используя встроенные средства среды Simulink, получим график переходного процесса системы, при воздействии на неё единичного ступенчатого сигнала (рис. 13). Из графика можем определить следующие параметры система автоматического управления: · величина статической ошибки – 0%; · время переходного процесса –30 с; · колебательность присутствует; · коэффициент перерегулирования – 55.5%. Исходя из этих данных, можно сделать вывод о том, что система автоматического управления не соответствует техническому заданию (по пунктам коэффициент перерегулирования, время переходного процесса и колебательность системы) и нуждается в корректировке. В качестве корректирующего звена выберем ПИД (пропорционально-интегрально-дифференциальный) регулятор.
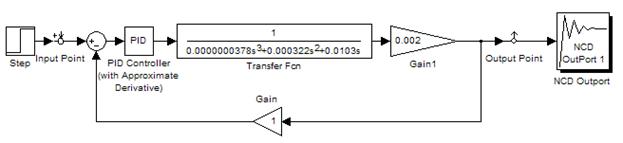
Рис. 13. График переходного процесса системы при воздействии на неё единичного ступенчатого сигнала Настройка ПИД - регулятора. Для настройки ПИД регулятора – определения значений пропорционального, дифференциального и интегрального коэффициентов – воспользуемся встроенными средствами среды Simulink. Подбор коэффициентов будем осуществлять с помощью блока NCD OutPort. Включим его в схему, как показано на рисунке 27.
Рис. 14. Схема, собранная для настройки ПИД регулятора Зададим настройки блока NCD OutPort (рис. 15 16) и ПИД регулятора PID Controller (рис. 17).
Рис. 15. Настройки блока NCD OutPort
Рис. 16. Настройки блока NCD OutPort
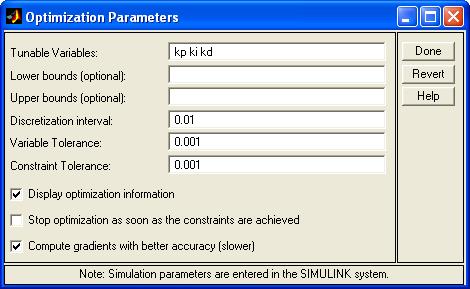
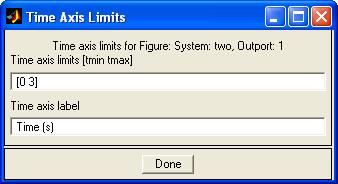
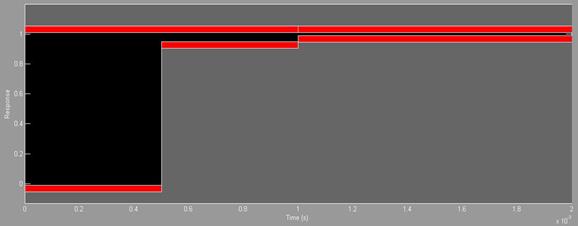
Рис. 17. Параметры ПИД регулятора PID Controller В блоке NCD OutPort зададим ограничения для графика переходного процесса (рис. 18). Блок NCD OutPort производит автоматическую коррекцию параметров Kp, Ki и Kd.
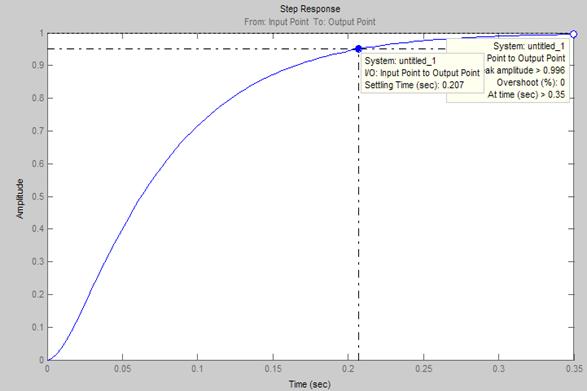
Рис. 18. Настройка границ в блоке NCD OutPort Значения коэффициентов, полученных оптимизацией в блоке NCD OutPort: Kp =64.48 Ki = 0, 025 Kd = 1, 12 После корректировки переходная функция удовлетворяет техническому заданию (рис. 19). Получены следующие характеристики: Время переходного процесса – 0.207 с. Количество колебаний – 0. Коэффициент перерегулирования – 0. Статическая ошибка – 0.004.
Рис. 19. Реакция системы на единичное ступенчатое воздействие Определение передаточных функций разомкнутой и замкнутой системы. Определим передаточную функцию разомкнутой системы: Wраз = Wус (p) ∙ Wдвигателя (p) ∙ Wредуктора (p) ∙ WПИД-регулятора (p) (12)
(13) Определим передаточную функцию замкнутой системы:
(15)
(16)
Характеристическое уравнение замкнутой системы имеет вид:
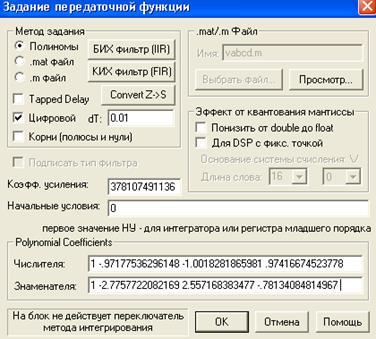
Моделирование цифровой системы. Для исследования ЦСАУ необходимо провести z-преобразование передаточной функции непрерывной системы. Для этого воспользуемся средствами математического пакета VisSim (рис. 20).
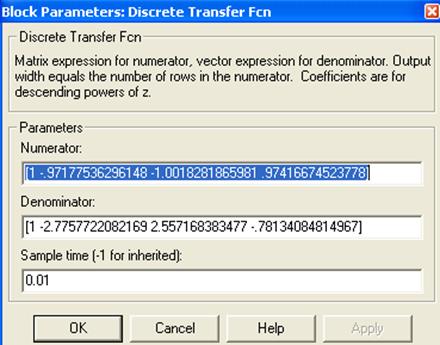
Рис. 20. Переход в Z-пространство средствами VisSim Итогом этого преобразования станет дискретная передаточная функция (рис. 21).
Рис. 21. Дискретная передаточная функция, полученная средствами VisSim Смоделируем схему цифровой и замкнутую системы автоматического управления в Simulink (рис. 22).
Рис. 22. Структурная схема цифровой и замкнутой системы.
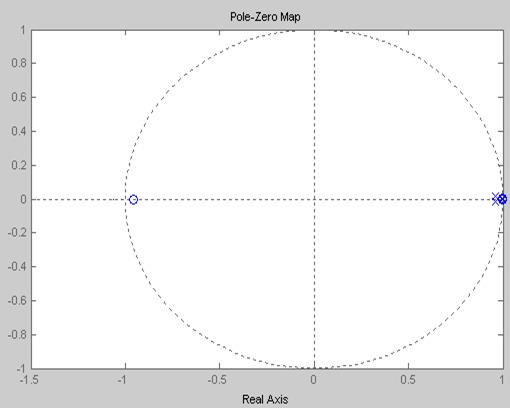
Исследование цифровой системы на устойчивость. Как известно, непрерывная система устойчива, если все корни ее характеристического уравнения лежат в левой полуплоскости. При исследовании дискретных систем вместо р используется новая переменная z =
Рис. 23. Проверка устойчивости ЦСАУ Как видно из рис. 23, все корни характеристического уравнения лежат внутри единичной окружности, следовательно, проектируемая цифровая система устойчива.
|
||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 273; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.221.114 (0.007 с.) |

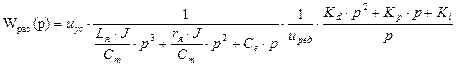
 (14)
(14)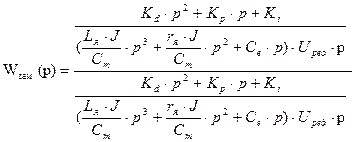
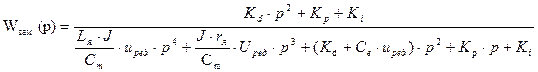
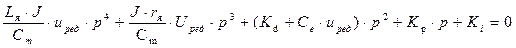 (17)
(17)

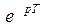 . Конформное преобразование z =
. Конформное преобразование z =