
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи к практическому занятию №9Содержание книги
Поиск на нашем сайте
Для совместной работы на доске
Задача 9.1 Для данной рамной конструкции подобрать из условия прочности в качестве поперечного сечения элементов двутавровый профиль, если жесткость сечений всех элементов одинакова
Для самостоятельной работы
Задача 9.2 Для данной рамной конструкции подобрать из условия прочности в качестве поперечного сечения элементов двутавровый профиль, если жесткость сечений всех элементов одинакова
Лабораторно-практическое занятие №6 При подготовке к лабораторно-практическому занятию использовать методическую литературу: Расчеты статически неопределимых систем в условиях изгиба: Лабораторный практикум / Составители: Е.П. Гордиенко, И.Т. Каратеева, И.В. Котова. – Тольятти: ТГУ, 2005. – 47 с. Расчетно-проектировочная работа №4 Задача 4.1. Расчет на прочность статически неопределимых стержней
На ступенчатый стальной брус круглого поперечного сечения с заданным соотношением площадей: А1=А, А2=А/2, А3=А/3 (РПР №2, задача 2.1) установили на свободном конце вторую жесткую заделку (все остальные исходные данные – прежние: см. табл. 2.1, стр. 53 Пособия, ч.I). Для полученного таким образом статически неопределимого стержня подобрать новые размеры поперечных сечений из условия прочности. Проанализировать влияние изменения жесткости стержня на его экономичность. Проверить прочность статически неопределимого стержня при дополнительном действии температуры или при наличии неточности изготовления. Принять коэффициент линейного расширения α=1,25´10‑5 1/°С, модуль упругости Е=2´105 МПа. Исходные данные по дополнительному фактору взять из табл. 4.1, используя вторую и третью цифру варианта.
План решения
1. Раскрыть статическую неопределимость стержня методом сил. 2. Из условия прочности подобрать новые размеры поперечных сечений. 3. Сравнить статически определимый и статически неопределимый стержни по экономичности. Сделать вывод. 4. Определить дополнительные напряжения в стержне, возникающие от неточности изготовления (или от действия температуры). 5. Проверить выполнение условия прочности стержня при одновременном действии заданной нагрузки и дополнительного фактора.
Таблица 4.1
Задача 4.2. Расчет на прочность и жесткость статически неопределимых рам
На статически определимой раме (РПР №1, задача 1.3, схема №3) установили дополнительные опоры (рис. 4.2, все остальные исходные данные – прежние: табл. 1.3 стр. 32 Пособия, ч.I). Материал стержня – Ст. 3: [σ]=160 МПа, Е=2×105 МПа. Жесткость сечений всех участков рамы постоянна: ЕIх=const. Для полученной таким образом статически неопределимой рамы подобрать рациональное поперечное сечение из условия прочности и проверить конструкцию на жесткость.
План решения
1. Раскрыть статическую неопределимость рамы методом сил. 2. Построить эпюры изгибающих моментов и продольных сил для заданной системы и провести проверку правильности решения. 3. Установить положение опасного сечения рамы и из условия прочности подобрать рациональное сечение. 4. Определить прогиб в месте предполагаемой наибольшей деформации, показав приближенный вид упругой линии рамы, и записать условие жесткости. 5*. Повторить п.3 для статически определимой рамы, сравнить результаты и сделать вывод о влиянии изменения жесткости рамы на ее экономичность.
Расчетные схемы статически неопределимых рам
Рис. 4.2. Расчетные схемы статически неопределимых рам.
Вариант контрольного теста Задание 1 (Добавьте ключевое слово) При раскрытии статической неопределимости методом сил в системе канонических уравнений за неизвестные принимаются … по направлению «лишних» связей
Задание 2 (Отметьте правильный ответ) Математическое выражение деформационной проверки для статически неопределимой системы при изгибе имеет вид: o o o o
Задание 3 (Добавьте число) Статически неопределимая система
имеет степень статической неопределимости S= …
Задание 4 (Отметьте правильный ответ) Статически неопределимая система:
является …
o симметричной системой с симметричной нагрузкой o симметричной системой с кососимметричной нагрузкой o кососимметричной системой с симметричной нагрузкой o кососимметричной системой с кососимметричной нагрузкой
Задание 5 (Отметьте правильный ответ) Для статически неопределимой балки:
нельзя использовать в качестве основной системы следующую:
Задание 6 (Отметьте правильный ответ) Эквивалентная система
соответствует следующей исходной статически неопределимой системе:
Задание 7 (Отметьте правильный ответ) Для единичной эпюры
коэффициент системы канонических уравнений
o o o o Модуль №8 Теоретический материал
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 304; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.229.217 (0.008 с.) |

 , [σ]=160 МПа. Определить горизонтальное перемещение узловых точек и построить примерный вид упругой линии рамы.
, [σ]=160 МПа. Определить горизонтальное перемещение узловых точек и построить примерный вид упругой линии рамы.
 , [σ]=160 МПа. Определить горизонтальное перемещение узловых точек и построить примерный вид упругой линии рамы.
, [σ]=160 МПа. Определить горизонтальное перемещение узловых точек и построить примерный вид упругой линии рамы.
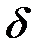 , % от длины
, % от длины
 , град
, град







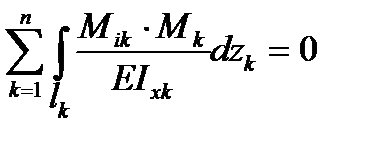














 :
:
 равен:
равен:






