
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема. Статически неопределимые системы.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте ПЗ_3. Расчет статически неопределимых конструкций
1. Статически неопределимые задачи Задачи на расчет конструкций, в элементах которых внутренние силовые факторы не могут быть определены при помощи одних уравнений Температурное удлинение (укорочение) стержня
где α - коэффициент линейного расширения материала стержня. Пример. Жесткая балка (рис.1) силой тяжести 40 кН шарнирно На балку действуют сосредоточенная сила Р=20кН. Площади Определить усилия в стержнях, а также возникающие в них
Рис. 1 Решение. Применяя к балке принцип освобождаемое™ от связей, Для полученной плоской уравновешенной системы сил можно Для решения задачи необходимо составить третье, дополнительное Из подобия треугольников АВВ1 и ADD1получим
Поскольку реакцию RА не требуется определять, то составим только одно уравнение равновесия - сумму моментов сил относительно точки А.
или По закону Гука.
Разделим первое равенство на второе
Тогда Находим реакции стержней:
R1= 6,3 кН;
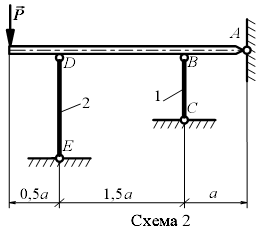
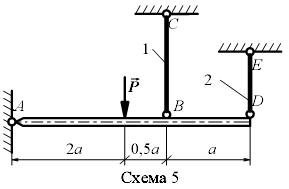
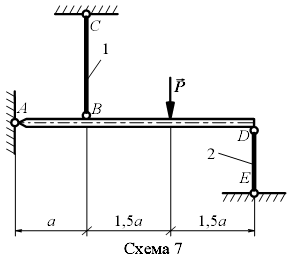
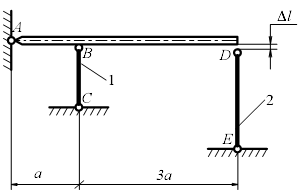
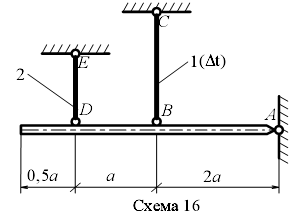
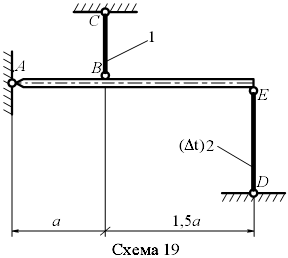
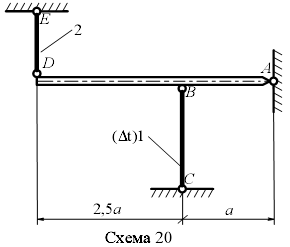
Задание 1.1. Определить усилия в стержнях жесткой балки и Удлинение стержня в зависимости от температуры ∆ l =α l ∆ T, где α = 12*10-6 К-1- коэффициент линейного расширения железа; ∆ T- изменение температуры стержня. Таблица 1
Рис.2
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 4 Тема. Геометрические характеристики плоских сечений Тема практического занятия: Определение положения центра тяжести плоского симметричного сечения Цель занятия: Определить положение центра тяжести сечения, составленного из профилей стандартного проката Последовательность решения задачи: 1) начертить заданное сложное сечение (фигуру), выбрать оси координат. 2) разбить сложное сечение на простые, для которых центры тяжести и силы тяжести известны; 3) определить необходимые данные для простых сечений: а) выписать из таблиц ГОСТа для каждого стандартного профиля необходимые справочные данные (h; b; d; A; для швеллера z 0) или определить площадь простого сечения; б) определить координаты центров тяжести простых сечений относительно выбранных осей координат; в) определить статические моменты площади простых сечений; 4) определить положение центра тяжести сложного сечения. Контрольные вопросы для студентов: 1. Каким свойством обладает центр параллельных сил? 2. Запишите формулы для определения центра тяжести плоской фигуры, составленной из площадей. 3. Что такое статический момент площади? 4. В каких единицах измеряется статический момент площади? 5. Какие свойством обладает статический момент площади? 6. Перечислите способы определения центра тяжести твердого тела. 7. Где находится центр тяжести тела, имеющего 2 оси симметрии? ЗАДАНИЯ ДЛЯ ПРАКТИЧЕСКОГО ЗАНЯТИЯ ЗАДАЧА. Для заданных плоских симметричных сечений, составленных из профилей стандартного проката определить: I) Положение центра тяжести; II) Главные центральные моменты инерции. Данные своего варианта взять из таблицы к ПЗ №4
Таблица ПЗ № 4
Обратите внимание, что, все геометрические параметры швеллера даны в ГОСТ при вертикальном положении его стенки. При повороте швеллера на угол 900, все его геометрические параметры заданные относительно оси Х меняются на параметры заданные относительно оси У. ПРИМЕР РЕШЕНИЯ Задача. Для заданного плоского симметричного сечения составленного из профилей стандартного проката определить положение центра тяжести Дано: полоса 120´10 (ГОСТ 103-76); двутавр № 12 (ГОСТ 8239-89); швеллер № 14 (ГОСТ 8240-89). Найти: С (х С; у С). Решение: 1) Разбиваем сложное сечение на 3 простых сечения: 1 – полоса; 2 – двутавр; 3 – швеллер. 2) Выписываем из таблиц ГОСТа и определяем необходимые данные для простых сечений: Полоса 120´10; А 1 =120·10=1200 мм 2 =12 см 2; С 1 (0;0,5) Двутавр № 12; А 2 =14,7 см 2 ; С 2 (0; 7) Швеллер № 14; А 3 =15,6 см 2 ; С 3 (0; 14,67) 3) Находим статические моменты площади относительно оси 0 х: S x1 = A 1 ·y1 =12·0,5=6 см 3; S x2 = A 2 ·y2 =14,7·7=102,9 см 3; S x3 = A 3 ·y3 =15,6·14,67=228,9 см 3; ∑ S х = S x1 + S x2 + S x3 =6+102,9+228,9=337,8 см 3. 4) Определяем сумму площадей простых сечений: ∑ А k = A 1+ A 2 + A 3 =12+14,7+15,6=42,3 см 2. 5) Определяем положение центра тяжести сложного сечения: х С =∑ S у\∑ А k; х С =0 см; у C =∑ S х\∑ А k; у C =337,8\42,3=8 см. Ответ: центр тяжести сложного сечения находится в точке С (0; 8). Литература: 1. Волков А. Н. Сопротивление материалов. — М.: КолосС, 2004. — С.36…41. 2. Кривошапко С. Н. Сопротивление материалов: лекции, семинары, расчетно-графические работы. — М.: Издательство Юрайт, 2013. — С.220…228.
Тема №5 программы: Геометрические характеристики плоских сечений Тема практического занятия: Определение главных центральных моментов инерции сложного симметричного сечения Цель занятия: Определить главные центральные моменты инерции сложного симметричного сечения, составленного из профилей стандартного проката Последовательность решения задачи: 1) провести центральные оси простых сечений у сложного сечения центр тяжести, которой известен; 2) определить необходимые данные для простых сечений: а) выписать из таблиц ГОСТа для каждого стандартного профиля необходимые справочные данные (J x i ; J у i ), определить центральные моменты инерции полосы; б) определить расстояния между главной центральной осью сложного сечения и центральными осями простых сечений по формуле: аi= |у С -у i |; 3) определить главные центральные моменты инерции сложного сечения. Контрольные вопросы для студентов: 1. Какая величина называется статическим моментом сечения? 2. Назовите свойство статического момента сечения относительно центральных осей. 3. Какие величины называются осевыми моментами инерции сечения, какие сечения они характеризуют? 4. Какая величина называется центробежным моментом инерции сечения, какие сечения они характеризуют? 5. Какая величина называется полярным моментом инерции сечений, какие сечения он характеризует? 6. Назовите свойство полярного момента инерции сечения. 7. Какие моменты инерции сечения и оси называются главными? 8. Какие моменты инерции сечения называются главными центральными? ПРИМЕР РЕШЕНИЯ Задача. Для плоского симметричного сечения составленного из профилей стандартного проката определить главные центральные моменты инерции (см. ПЗ № 4) Дано: полоса 120´10 (ГОСТ 103-76); двутавр № 12 (ГОСТ 8239-89); швеллер № 14 (ГОСТ 8240-89); центр тяжести сечения: С (0; 8). НАЙТИ: J x; J у. Решение II: 1) Провести центральные оси простых сечений. 2) Выписываем из таблиц ГОСТа и определяем центральные моменты инерции для простых сечений: Полоса 120´10; А 1=12 см2; С 1 (0;0,5); J x1= b · h 3/12=12·13/12=1 см4; J у1= b 3· h =123·1/12=144 см4. Двутавр № 12; А 2 =14,7 см 2 ; С 2 (0; 7); J x2=350 см4; J у2=27,9 см4. Швеллер № 14; А 3 =15,6 см 2 ; С 3 (0; 14,67); J x3=45,4 см4; J у3=491 см4 3) Определяем расстояния между главной центральной осью сложного сечения и центральными осями простых сечений: а 1=|у С -у1|=8-0,5=7,5 см; а 2=|у С -у2|=8-7=1 см; а 3=|у С -у3|=|8-14,67|=6,67 см. 4) Определяем главный центральный момент инерции сложного сечения относительно оси у по формуле: J у =∑ J у i = J у1+ J у2+ J у3=144+27,9+491=662,9 см4. 5) Определяем главный центральный момент инерции сложного сечения относительно оси х по формуле: J хС=∑(J х i+аi 2· Аi)=(J х1 +а 12· А 1)+(J х2 +а 22· А 2)+(J х3 +а 32· А 3); J хС=(1+7,52·12)+(350+12·14,7)+(45,4+6,672·15,6)=1780,1 см4. Ответ: J max= J xС=1780,1 см4; J min= J у=662,9 см4. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №6
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 693; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.190.247 (4.019 с.) |

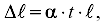
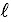 .
.

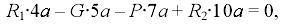



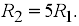


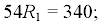

















 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 5
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 5


