Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра «Технологические и транспортные машины и комплексы»Содержание книги
Поиск на нашем сайте
ТВЕРСКАЯ ГОСУДАРСТВЕННАЯ СЕЛЬСКОХОЗЯЙСТВЕННАЯ АКАДЕМИЯ Кафедра «Технологические и транспортные машины и комплексы»
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Методические указания к практическим занятиям
Тверь 2016
Рецензент: профессор кафедры ремонта и эксплуатации МТП Берней В.И.
Елисеев Ю.В. СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ: Методические указания к практическим занятиям. Растяжение и сжатие/Ю.В. Елисеев, А.В. Кудрявцев –Тверь: ТГСХА, 2016.- 56 с.
В методических указаниях даны рекомендации по подготовке к практическим занятиям. Предназначены для студентов инженерных направлений: 35.03.06-«Агроинженерия» (профиль «Технические системы в агробизнесе»), 23.03.03- « Эксплуатация транспортно-технологических машин и комплексов» (профиль «Автомобильный сервис») и специальности 23.05.01- «Наземные транспортно-технологические средства» (специализация «Автомобили и тракторы»).
Рекомендовано к изданию на заседании кафедры ТТМиК: Протокол №2 от 2. 09. 2016г.
Рекомендовано к изданию методической комиссией инженерного факультета: Протокол №1 от 14.09. 2016г. ОСНОВНЫЕ ОБОЗНАЧЕНИЯ m – масса; F (F x, F y, F z) – сила (составляющие силы по координатным осям); М – момент силы (момент пары); q – интенсивность распределенной нагрузки; R (X, Y, Z)– реакция (реактивная сила); M R – реактивный момент в жесткой заделке; T – сила натяжения гибкой связи (каната, троса, ремня); F ∑ – равнодействующая сила; М ∑ – равнодействующий момент; F т – сила трения; M т – момент трения; G – сила тяжести; F и – сила инерции; f – коэффициент трения скольжения; А – площадь; S x – статический момент площади относительно оси х; V – объем; С – центр тяжести; W – работа силы (момента силы); P – мощность силы (момента силы); l (l AB) – длина (длина между точками A и В); t – время; s – перемещение, путь; v – скорость; а – ускорение; a n (a t) – нормальное (тангенциальное) ускорение; j – угол поворота; w – угловая скорость; рад/с e – угловое ускорение; n – частота вращения вала, об/мин; h – коэффициент полезного действия (КПД).
[s] – допускаемое нормальное напряжение (общее обозначение); [sр] – то же, при растяжении; [sс] – то же, при сжатии; [sсм] – то же, при смятии;
sВ – предел прочности; sВр (sВс) – предел прочности при растяжении (при сжатии); sт – предел текучести; smax (tmax) – наибольшее напряжение в поперечном сечении бруса; sпц – предел пропорциональности; [t] – допускаемое касательное напряжение; [tкр] – допускаемое напряжение при кручении; [tср] – то же, при срезе; j – угол закручивания бруса при кручении; [ j 0] – допускаемый относительный угол закручивания; Е – модуль продольной упругости; J x, J y – главные центральные моменты инерции; J p – полярный момент инерции; М х, – изгибающий момент в поперечном сечении бруса относительно оси х; М изг – изгибающий момент, суммарный для бруса круглого поперечного сечения; М кр – крутящийся момент в поперечном сечении бруса; N, – продольная сила в поперечном сечении бруса; s [ s ] – коэффициент запаса прочности (нормативный); Q y, Q – поперечная сила, действующая вдоль оси у или суммарная.
СОДЕРЖАНИЕ 1.Тема. Введение. Основные определения. ПЗ_1. Определение реакций опор балок………………………………………………………………………………..5 2.Тема. Центральное растяжение (сжатие). ПЗ_2. Расчет бруса на растяжение (сжатие)……………………………………………………………………………..8 3.Тема. Статически неопределимые системы. ПЗ_3. Расчет статически неопределимых конструкций…………………………………………………….14 4. Тема. Геометрические характеристики плоских сечений. ПЗ_4. Определение положения центра тяжести плоского симметричного сечения………………..19 5.Тема. Геометрические характеристики плоских сечений. ПЗ_5.Определение главных центральных моментов инерции сложного симметричного сечения..22 6.Тема. Сложное напряженное состояние. ПЗ_6. Сложное напряженное состояние…………………………………………………………………………..25 7.Тема. Кручение. Стержни круглого поперечного сечения. ПЗ_7.Расчет вала на кручение……………………………………………………………………………35 8.Тема. Изгиб плоский прямой. ПЗ_8. Определение размеров поперечного сечения консольной балки………………………………………………………...42 9.Тема. Сложное сопротивление. ПЗ_9. Определение диаметра вала при изгибе с кручением……………………………………………………………………….….46 Приложения…………………………………………………………………….…..51
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №1 Тема. Введение. Основные определения Тема практического занятия: Определение реакций опор балок Цель занятия: Определить реакции опор консольной балки Последовательность решения задачи: 1) изобразить балку с действующими на нее нагрузками; 2) составить расчетную схему балки: 3) выбрать расположение координатных осей; 4) произвести необходимые преобразования заданных сил: – наклоненную к оси балки под углом – равномерно распределенную нагрузку – ее равнодействующей; 5) освободить балку от опор, заменив их действие реакциями; 6) составить и решить уравнения равновесия заданной системы сил; 7) провести проверку решения. Контрольные вопросы для студентов: 1. Какие разновидности связей рассматриваются в статике? 2. Как определяется проекция силы на ось? 3. Назовите единицы измерения силы? 4. Как определяется момент силы относительно точки? 5. Назовите единицы измерения момента силы? 6. Назовите правило знаков для определения момента силы относительно точки? 7. Чем отличаются активные силы от пассивных? 8. Запишите уравнения равновесия для системы произвольных сил? 9. Как определяется равнодействующая равномерно распределенной нагрузки? 10. Какая разновидность связи была задана в условии задачи? ЗАДАНИЯ ДЛЯ ПРАКТИЧЕСКОГО ЗАНЯТИЯ ЗАДАЧА. Жестко заделанная консольная балка нагружена равномерно распределенной нагрузкой интенсивностью q и моментом М. На расстоянии а от стены передается сила F, наклоненная к оси балки под углом α. Определить реакции заделки. Данные своего варианта взять из таблицы ПЗ № 1
Таблица ПЗ № 1
Примечание. Схема: для четных вариантов – а); для нечетных – б). ПРИМЕР РЕШЕНИЯ ПЗ № 1 Задача. Жестко заделанная консольная балка АВ нагружена, как показано на рис. ПЗ №1, а. Определить реакции заделки балки ДАНО: F=50 кН; q=5 кН/м; М=20 кН·м; α=200. НАЙТИ: RА, φх, МЗ. РЕШЕНИЕ: 1) Изображаем балку (см. рис. ПЗ №1). 2) Составляем расчетную схему балки: · провести оси координат х и у; · найти модули проекций силы F: F х= F ·cosα; F х =50·cos200=50·0,9397=47 кН; F у= F ·sinα; F у =50·sin200=50·0,342=17,1 кН; · определяем равнодействующую равномерно распределенной нагрузки и расстояние от ее линии действия до опоры А: F q= q · l = q · AB =5·5=25 кН; АК = l /2= АВ /2=2,5 м; · применяем принцип освобождения тела от связей (см. рис. ПЗ №1, б). 3)Составляем уравнения равновесия и определяем неизвестные реакции опор: ∑ Fk x=0, RA x+ F x=0, RA x=- F x=-47 кН; ∑ Fk y=0, RA y- F q+ F y=0, RA y= F q- F y=25-17,1=7,9 кН;
∑ MA (Fk)=0, M З+ F q· AK - F y· AC - M =0, M З=- F q· AK + F y· AC + M =-25·2,5+17,1·2+20=-8,3 кН·м. 4) Проверяем правильность найденных результатов: MC (Fk)= RA y· AC + M З+ F q· CK - M =7,9·2–8,3+25·0,5-20=0; Ответ: RA=47,7 кH; φх=9,50; MЗ=-8,3 кН·м.
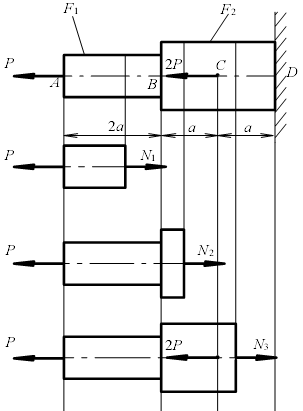
ПРАКТИЧЕСКЕ ЗАНЯТИЕ № 2 Общие сведения Растяжением или сжатием называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только продольная сила. Продольная сила в поперечном сечении бруса численно равна алгебраической сумме внешних сил, расположенных по одну сторону сечения (имеется в виду, что все силы направлены вдоль оси бруса). Растягивающие (направленные от сечения) продольные силы считаются положительными, а сжимающие (направленные к сечению) – отрицательными. При растяжении и сжатии в поперечных сечениях бруса возникают только нормальные напряжения, равномерно распределенные по сечению и вычисляемые по формуле
где N − продольная сила; F − площадь поперечного сечения. Для наглядного изображения распределения вдоль оси бруса продольных сил и нормальных напряжений строят графики, называемые эпюрами. Деформацией при растяжении участка бруса является его удлинение. Абсолютное удлинение или укорочение прямо пропорционально продольной силе, длине участка бруса и обратно пропорционально
где EF − жесткость сечения. Коэффициент E характеризует жесткость материала, т. е. его способность сопротивляться упругим деформациям растяжения или сжатия и называется модулем упругости первого рода; для стали E = (1,96…2,16)·105Па. 1.2 Пример. Построить эпюры продольных сил, нормальных напряжений и перемещений поперечных сечений по длине ступенчатого бруса (рис. 1). Материал бруса – сталь Ст.3; E = 2 ⋅105МПа; P = 60 кН; F 1 = 5 см2; F 2= 12 см2; a = 1м. Решение. Разбиваем брус на участки 1(АВ), 2(ВС) и 3(CD). Применяя метод сечений, рассматриваем равновесие левой части, отбрасывая при этом отсеченную правую часть
Для участка 1 N 1= P = 60кН; Для участка 2 N 2= P = 60кН; Для участка 3 N 3= P +2 P =3 P =180кН. Эпюра, показывающая, как меняется N по длине бруса, изображена на рис. 1.
Для построения эпюры нормальных напряжений, находим напряжения на каждом участке:
Рис.1.1
Эпюру перемещений строим, начиная от защемленного конца D. Перемещение поперечного сечения, где проложена сила 2 P (точка С), равное удлинению участка CD.
Перемещение сечения В относительно сечения С равно удлинению участка ВС.
Абсолютное перемещение сечения В: Δ B = Δ C + Δ BC = 0,75 + 0,25 =1,0мм. Перемещение сечения А относительно В, равное удлинению
участка АВ:
Абсолютное перемещение сечения А:
Δ A = Δ B + Δ AB = 1,0 + 1,2 = 2,2мм. Построенная по полученным данным эпюра перемещений показана на рис. 1.
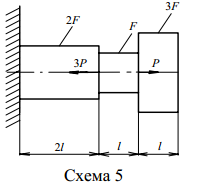
1.3 Задание 1. Вариант 1. Построить эпюры продольных сил, нормальных напряжений и перемещений поперечных сечений по длине ступенчатого бруса по данным одной из схем, приведенных на рисунках 1.2. Вариант 1 Исходные данные: P = 50 кН; F = 5 см2; l = 1 м.
Рис.1.2
Вариант 2 Для стального бруса, нагруженного продольными силами Р, с учетом собственного веса (рис.1.3) требуется: 1. Определить внутренние силы, напряжения и перемещения по длине бруса. 2. Построить эпюры нормальных сил, напряжений и перемещений по длине бруса. 3. Указать положение наиболее опасного сечения и величину нормального напряжения в этом сечении. Принять, что материал бруса имеет плотность γ = 7,8 г/см3 и модуль продольной упругости Е = 2•105 МПа. Таблица 1.1 – Исходные данные
Рис. 1.3
Литература: 1. Волков А. Н. Сопротивление материалов. — М.: КолосС, 2004. — С.18…19. 2. Кривошапко С. Н. Сопротивление материалов: лекции, семинары, расчетно-графические работы. — М.: Издательство Юрайт, 2013. — С.187…194.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №3
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 4 Тема. Геометрические характеристики плоских сечений Тема практического занятия: Определение положения центра тяжести плоского симметричного сечения Цель занятия: Определить положение центра тяжести сечения, составленного из профилей стандартного проката Последовательность решения задачи: 1) начертить заданное сложное сечение (фигуру), выбрать оси координат. 2) разбить сложное сечение на простые, для которых центры тяжести и силы тяжести известны; 3) определить необходимые данные для простых сечений: а) выписать из таблиц ГОСТа для каждого стандартного профиля необходимые справочные данные (h; b; d; A; для швеллера z 0) или определить площадь простого сечения; б) определить координаты центров тяжести простых сечений относительно выбранных осей координат; в) определить статические моменты площади простых сечений; 4) определить положение центра тяжести сложного сечения. Контрольные вопросы для студентов: 1. Каким свойством обладает центр параллельных сил? 2. Запишите формулы для определения центра тяжести плоской фигуры, составленной из площадей. 3. Что такое статический момент площади? 4. В каких единицах измеряется статический момент площади? 5. Какие свойством обладает статический момент площади? 6. Перечислите способы определения центра тяжести твердого тела. 7. Где находится центр тяжести тела, имеющего 2 оси симметрии? ЗАДАНИЯ ДЛЯ ПРАКТИЧЕСКОГО ЗАНЯТИЯ ЗАДАЧА. Для заданных плоских симметричных сечений, составленных из профилей стандартного проката определить:
I) Положение центра тяжести; II) Главные центральные моменты инерции. Данные своего варианта взять из таблицы к ПЗ №4
Таблица ПЗ № 4
Обратите внимание, что, все геометрические параметры швеллера даны в ГОСТ при вертикальном положении его стенки. При повороте швеллера на угол 900, все его геометрические параметры заданные относительно оси Х меняются на параметры заданные относительно оси У. ПРИМЕР РЕШЕНИЯ Задача. Для заданного плоского симметричного сечения составленного из профилей стандартного проката определить положение центра тяжести Дано: полоса 120´10 (ГОСТ 103-76); двутавр № 12 (ГОСТ 8239-89); швеллер № 14 (ГОСТ 8240-89). Найти: С (х С; у С). Решение: 1) Разбиваем сложное сечение на 3 простых сечения: 1 – полоса; 2 – двутавр; 3 – швеллер. 2) Выписываем из таблиц ГОСТа и определяем необходимые данные для простых сечений: Полоса 120´10; А 1 =120·10=1200 мм 2 =12 см 2; С 1 (0;0,5) Двутавр № 12; А 2 =14,7 см 2 ; С 2 (0; 7) Швеллер № 14; А 3 =15,6 см 2 ; С 3 (0; 14,67) 3) Находим статические моменты площади относительно оси 0 х: S x1 = A 1 ·y1 =12·0,5=6 см 3; S x2 = A 2 ·y2 =14,7·7=102,9 см 3; S x3 = A 3 ·y3 =15,6·14,67=228,9 см 3; ∑ S х = S x1 + S x2 + S x3 =6+102,9+228,9=337,8 см 3. 4) Определяем сумму площадей простых сечений: ∑ А k = A 1+ A 2 + A 3 =12+14,7+15,6=42,3 см 2. 5) Определяем положение центра тяжести сложного сечения: х С =∑ S у\∑ А k; х С =0 см; у C =∑ S х\∑ А k; у C =337,8\42,3=8 см. Ответ: центр тяжести сложного сечения находится в точке С (0; 8). Литература: 1. Волков А. Н. Сопротивление материалов. — М.: КолосС, 2004. — С.36…41. 2. Кривошапко С. Н. Сопротивление материалов: лекции, семинары, расчетно-графические работы. — М.: Издательство Юрайт, 2013. — С.220…228.
Тема №5 программы: Геометрические характеристики плоских сечений Тема практического занятия: Определение главных центральных моментов инерции сложного симметричного сечения Цель занятия: Определить главные центральные моменты инерции сложного симметричного сечения, составленного из профилей стандартного проката Последовательность решения задачи: 1) провести центральные оси простых сечений у сложного сечения центр тяжести, которой известен; 2) определить необходимые данные для простых сечений: а) выписать из таблиц ГОСТа для каждого стандартного профиля необходимые справочные данные (J x i ; J у i ), определить центральные моменты инерции полосы; б) определить расстояния между главной центральной осью сложного сечения и центральными осями простых сечений по формуле: аi= |у С -у i |; 3) определить главные центральные моменты инерции сложного сечения. Контрольные вопросы для студентов: 1. Какая величина называется статическим моментом сечения? 2. Назовите свойство статического момента сечения относительно центральных осей. 3. Какие величины называются осевыми моментами инерции сечения, какие сечения они характеризуют? 4. Какая величина называется центробежным моментом инерции сечения, какие сечения они характеризуют? 5. Какая величина называется полярным моментом инерции сечений, какие сечения он характеризует? 6. Назовите свойство полярного момента инерции сечения. 7. Какие моменты инерции сечения и оси называются главными? 8. Какие моменты инерции сечения называются главными центральными? ПРИМЕР РЕШЕНИЯ Задача. Для плоского симметричного сечения составленного из профилей стандартного проката определить главные центральные моменты инерции (см. ПЗ № 4) Дано: полоса 120´10 (ГОСТ 103-76); двутавр № 12 (ГОСТ 8239-89); швеллер № 14 (ГОСТ 8240-89); центр тяжести сечения: С (0; 8). НАЙТИ: J x; J у. Решение II: 1) Провести центральные оси простых сечений. 2) Выписываем из таблиц ГОСТа и определяем центральные моменты инерции для простых сечений: Полоса 120´10; А 1=12 см2; С 1 (0;0,5); J x1= b · h 3/12=12·13/12=1 см4; J у1= b 3· h =123·1/12=144 см4. Двутавр № 12; А 2 =14,7 см 2 ; С 2 (0; 7); J x2=350 см4; J у2=27,9 см4. Швеллер № 14; А 3 =15,6 см 2 ; С 3 (0; 14,67); J x3=45,4 см4; J у3=491 см4 3) Определяем расстояния между главной центральной осью сложного сечения и центральными осями простых сечений: а 1=|у С -у1|=8-0,5=7,5 см; а 2=|у С -у2|=8-7=1 см; а 3=|у С -у3|=|8-14,67|=6,67 см. 4) Определяем главный центральный момент инерции сложного сечения относительно оси у по формуле: J у =∑ J у i = J у1+ J у2+ J у3=144+27,9+491=662,9 см4. 5) Определяем главный центральный момент инерции сложного сечения относительно оси х по формуле: J хС=∑(J х i+аi 2· Аi)=(J х1 +а 12· А 1)+(J х2 +а 22· А 2)+(J х3 +а 32· А 3); J хС=(1+7,52·12)+(350+12·14,7)+(45,4+6,672·15,6)=1780,1 см4. Ответ: J max= J xС=1780,1 см4; J min= J у=662,9 см4. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №6 Общие сведения Напряжения в сечениях Напряжением называют меру воздействия внутренних силовых факторов на единицу площади в рассматриваемой точке сечения бруса. Система приложенных к телу внешних нагрузок, приводит к возникновению в его сечениях внутренних силы R и момента M.
При этом внутренняя сила и внутренний момент воздействуют на все сечение бруса в целом. Выделим в рассматриваемом сечении элементарную площадку dA бесконечно малой площади.
Полное напряжение – часть внутренних усилий, приходящаяся на конкретную точку сечения.
Обозначение полного напряжения в точке – p Единица измерения – Паскаль [Па] (Н/м2) Ввиду того, что большинство конструкционных материалов обладает высокой прочностью часто напряжения, возникающие в них, измеряются в кратных величинах, например, мегапаскаль [МПа]. В общем случае вектор полного напряжения в точке может располагаться под любым углом к сечению. В таких случаях для существенного упрощения расчетов его удобно раскладывать на составляющие (проекции):
σ – нормальное напряжение; τ – касательное напряжение В частных случаях (например, при растяжении-сжатии и кручении) в сечениях бруса имеют место только нормальные либо только касательные напряжения. При решении таких задач, величина нормальных и касательных напряжений сравнивается с соответствующими допустимыми значениями напряжений. Главные напряжения Главными называют нормальные напряжения на площадках выделенного элемента с нулевыми касательными напряжениями.
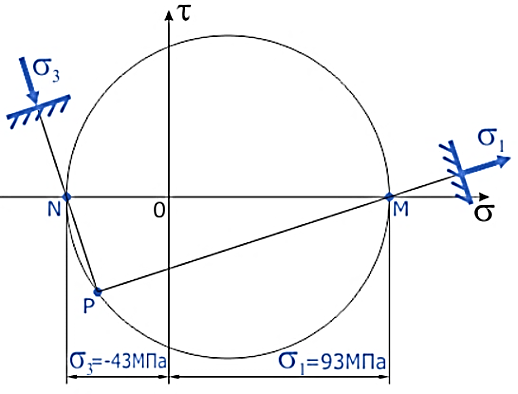
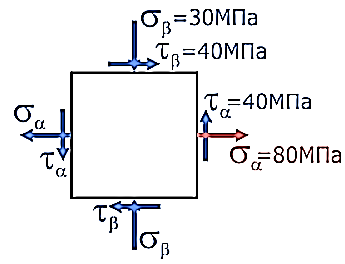
Для любого случая нагружения бруса всегда можно найти такое положение мысленно выделенного в нем элементарного объема, на гранях которого касательные напряжения будут отсутствовать (т.е. τ=0). Площадки (грани элемента) на которых касательные напряжения равны нулю называются главными. Таким образом, главные – это нормальные напряжения на главных площадках. Пример построения круга Мора по главным напряжениям. Для построения круга потребуются нормальные и касательные напряжения с двух любых взаимно перпендикулярных площадок (например, правой и верхней) при этом ось σ системы направляется вдоль большего (с учетом знака) из нормальных напряжений. Известны направления и значения нормальных и касательных напряжений.
Решение Круг Мора строится в плоской системе координат σ-τ. Начнем с правой площадки элемента.
Из конечной точки отрезка отложим вдоль оси τ значение соответствующего касательного напряжения τα=40МПа так же с учетом знака.
На конце последнего отрезка отметим точку, обозначив ее буквой A.
Аналогично для верхней площадки элемента.
Согласно закона парности касательных напряжений, точки A и B всегда будут расположены по разные стороны от оси σ и равноудалены от нее. Для главных напряжений (при отсутствии касательных) точки A и B останутся на оси нормальных напряжений. Полученные точки A и B соединяем отрезком.
На отрезке AB как на диаметре вычерчиваем окружность, с центром в точке пересечения отрезка AB с осью σ системы координат. Круг Мора построен. Множество точек полученной окружности показывают величину и знак нормальных и касательных напряжений при соответствующем положении площадок элемента. Точки пересечения круга Мора с осью σ показывают величину и знаки главных напряжений.
3.Пример. Задача Определить величину, знак и направление главных напряжений с помощью круга Мора по заданным нормальным и касательным напряжениям на гранях элемента.
Пример решения Используем построение круга Мора в пункте 6.2 решения задачи.
В данном случае главные напряжения в точке элемента составляют
Для определения направления главных напряжений выполним следующие действия: Из точки A проводим луч влево, а из точки B вниз до пересечения.
Луч, проведенный из полюса через точку М, показывает направление главного напряжения σ1.
Так как точка M расположена в области положительных значений σ то пго правилу знаков соответствующее главное напряжение будет растягивающим (стрелка напряжения направляется от площадки).
Аналогично, луч [PN) показывает направление главного напряжения на смежной площадке элемента.
Расположение точки N слева от пересечения осей σ-τ указывает на то, что это напряжение сжимающее (стрелка напряжения направлена в сторону площадки). Покажем полученные напряжения на заданном элементе. Для наглядности, главные площадки изображаются в пределах заданного элемента.
Здесь видно, что в сечении элемента расположенном под углом φ к начальному, касательные напряжения исчезают, а нормальные изменив величину, становятся главными.
Задание Элемент конструкции находится под действием сил, создающих напряженное состояние (рис. 1). Требуется: 1. Определить главные напряжения. 2. Определить направление главных площадок с помощью круга Мора. 3. Определить максимальные касательные напряжения. 4. Записать обобщенный закон Гука и определить линейные относительные деформации и относительное изменение объема. 5. Определить полную удельную потенциальную энергию упругой деформации. Модуль продольной упругости Е и коэффициент Пуассона μ материала заданы. Исходные данные приведены в таблице 6.1. Таблица 1 – Исходные данные
Рис. 1
Литература: 1. Волков А. Н. Сопротивление материалов. — М.: КолосС, 2004. — С.62…65. 2. Кривошапко С. Н. Сопротивление материалов: лекции, семинары, расчетно-графические работы. — М.: Издательство Юрайт, 2013. — С.27…31. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №7 Тема.Кручение Тема ПЗ_7. Расчет вала на кручение Общие сведения
Кручением называется такой вид деформации, при котором в любом поперечном сечении бруса возникают только крутящие моменты. Причиной деформации при кручении является внешний вращающий момент, приложенный в плоскости, перпендикулярной оси бруса. Для наглядного изображения распределения крутящих моментов вдоль оси бруса строится эпюра крутящих моментов. Крутящий момент в любом поперечном сечении численно равен алгебраической сумме внешних моментов, приложенных к брусу справа или слева от сечени
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 615; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.19.89 (0.014 с.) |

 силу F, заменить двумя взаимноперпендикулярными составляющими,
силу F, заменить двумя взаимноперпендикулярными составляющими, =47,7 кН;
=47,7 кН;  =arcsin0,166=9,50;
=arcsin0,166=9,50;
 жесткости сечения бруса
жесткости сечения бруса


























 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 5
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 5







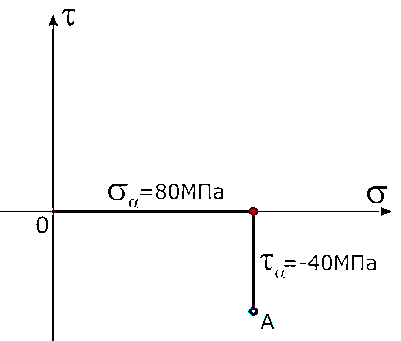



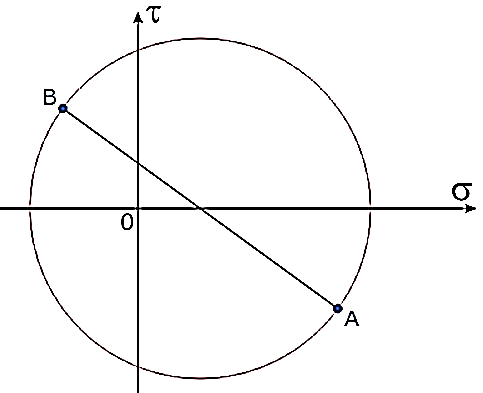

 Как было показано ранее, координаты точек пересечения круга Мора с осью напряжений σ показывают величину главных напряжений.
Как было показано ранее, координаты точек пересечения круга Мора с осью напряжений σ показывают величину главных напряжений.
 Точка их пересечения обозначается буквой P и является полюсом круга Мора. Очевидно, она будет располагаться на окружности.
Точка их пересечения обозначается буквой P и является полюсом круга Мора. Очевидно, она будет располагаться на окружности.