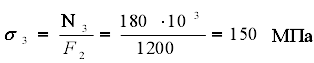Тема. Центральное растяжение (сжатие)

Задача № 1 Расчет бруса на растяжение (сжатие).

Общие сведения

Растяжением или сжатием называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только продольная сила. Продольная сила в поперечном сечении бруса численно равна алгебраической сумме внешних сил, расположенных по одну сторону сечения (имеется в виду, что все силы направлены вдоль оси бруса).

Растягивающие (направленные от сечения) продольные силы считаются положительными, а сжимающие (направленные к сечению) – отрицательными.

При растяжении и сжатии в поперечных сечениях бруса возникают только нормальные напряжения, равномерно распределенные по сечению и вычисляемые по формуле

 

где N − продольная сила; F − площадь поперечного сечения.

Для наглядного изображения распределения вдоль оси бруса

продольных сил и нормальных напряжений строят графики, называемые эпюрами.

Деформацией при растяжении участка бруса является его удлинение. Абсолютное удлинение или укорочение прямо пропорционально продольной силе, длине участка бруса и обратно пропорционально

жесткости сечения бруса

 

 

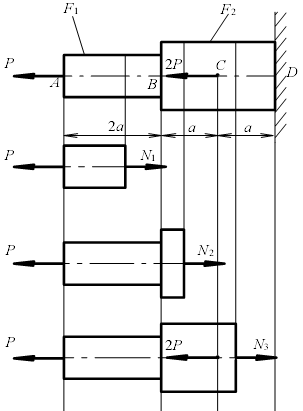
где EF − жесткость сечения.

Коэффициент E характеризует жесткость материала, т. е. его способность сопротивляться упругим деформациям растяжения или сжатия и называется модулем упругости первого рода; для стали

E = (1,96…2,16)·105Па.

1.2 Пример. Построить эпюры продольных сил, нормальных

напряжений и перемещений поперечных сечений по длине ступенчатого

бруса (рис. 1). Материал бруса – сталь Ст.3; E = 2 ⋅105МПа; P = 60 кН;

F 1 = 5 см2; F 2= 12 см2; a = 1м.

Решение. Разбиваем брус на участки 1(АВ), 2(ВС) и 3(CD).

Применяя метод сечений, рассматриваем равновесие левой части, отбрасывая при этом отсеченную правую часть

 

Для участка 1 N 1= P = 60кН;

Для участка 2 N 2= P = 60кН;

Для участка 3 N 3= P +2 P =3 P =180кН.

Эпюра, показывающая, как меняется N по длине бруса, изображена на рис. 1.

 

Для построения эпюры нормальных напряжений, находим напряжения на каждом участке:

 

Рис.1.1

 

 

Эпюру перемещений строим, начиная от защемленного конца D. Перемещение поперечного сечения, где проложена сила 2 P (точка С), равное удлинению участка CD.

Перемещение сечения В относительно сечения С равно удлинению участка ВС.

Абсолютное перемещение сечения В:

Δ B = Δ C + Δ BC = 0,75 + 0,25 =1,0мм.

Перемещение сечения А относительно В, равное удлинению

 

участка АВ:

Абсолютное перемещение сечения А:

Δ A = Δ B + Δ AB = 1,0 + 1,2 = 2,2мм.

Построенная по полученным данным эпюра перемещений

показана на рис. 1.

 

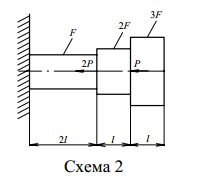
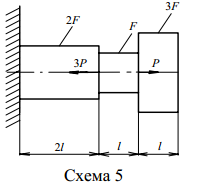
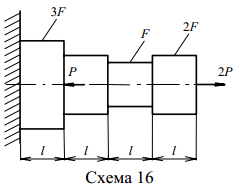
1.3 Задание 1. Вариант 1. Построить эпюры продольных сил, нормальных напряжений и перемещений поперечных сечений по длине ступенчатого бруса по данным одной из схем, приведенных на рисунках 1.2.

Вариант 1

Исходные данные: P = 50 кН; F = 5 см2; l = 1 м.

 

 

Рис.1.2

 

Вариант 2

Для стального бруса, нагруженного продольными силами Р, с учетом собственного веса (рис.1.3) требуется:

1. Определить внутренние силы, напряжения и перемещения по длине бруса.

2. Построить эпюры нормальных сил, напряжений и перемещений по длине бруса.

3. Указать положение наиболее опасного сечения и величину нормального напряжения в этом сечении.

Принять, что материал бруса имеет плотность γ = 7,8 г/см³ и модуль продольной упругости Е = 2•10⁵ МПа.

Таблица 1.1 – Исходные данные

 

№ варианта	Р, кН	F, м^2	a, м	b, м	c, м
	1,2	16•10 ^- 4	1,1	1,2	1,3
	1,9	13•10 ^- 4	1,4	1,7	1,5
	1,7	11•10 ^- 4	1,7	1,5	1,7
	1,3	15•10 ^- 4	2,0	1,9	1,8
	1,5	17•10 ^- 4	2,3	2,2	2,0
	2,0	19•10 ^- 4	2,6	2,5	2,4
	1,1	18•10 ^- 4	2,9	2,8	2,7
	1,6	14•10 ^- 4	1,5	1,6	1,6
	1,8	12•10 ^- 4	1,8	1,8	1,9
	2,2	10•10 ^- 4	1,2	1,3	1,4

 

Рис. 1.3

 

Литература:

1. Волков А. Н. Сопротивление материалов. — М.: КолосС, 2004. —

С.18…19.

2. Кривошапко С. Н. Сопротивление материалов: лекции, семинары, расчетно-­графические работы. — М.: Издательство Юрайт, 2013. — С.187…194.

 

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №3