
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напряжение и деформация при растяжение и сжатии.Содержание книги
Поиск на нашем сайте
Отношение приращения (изменения) длины элемента к его первоначально длине называется относительным удлинением или продольной деформацией. () Отношение изменения дельтаразмера поперечного сечения к его первоначальному значению называют относительным поперечным сужением (расширением) или поперечной деформацией: () В известных пределах нагружения между продольной деформацией и соответствующим (действующим в ее направлении) нормальным напряжением существует прямо пропорциональная (линейная зависимость). () Коэффициент пропорциональности Е называют модулем продольной упругости. При растяжение (сжатии) бруса в его поперечных сечениях возникают только нормальные напряжения. Сечения бруса, плоские и нормальные к его оси до деформации, остаются плоскими и нормальными к оси и при деформации. При растяжение (сжатии) бруса нормальные напряжения распределены по его поперечному сечению равномерно. При растяжении считают напряжения положительным. Распределение напряжений существенно зависит от способа приложения внешних сил лишь вблизи места нагружения. В частях, достаточно удлиненных от места приложения сил, распределение напряжений практически зависит только от статического эквивалента этих сил, а нет от способа их приложения.
Внутренний силовой фактор – Ƈ= Если N – «+» то растяжение Если N– «-» то сжатие l-длина бруса до деформации ∆l – абсолютное удлинение.
Закон Гука при растяжении и сжатии. Для подавляющего большинства конструкционных материалов с достаточной для практики точностью можно считать что: В известных пределах нагружения между продольной деформацией и соответствующим (действующим в ее направлении) нормальным напряжением существует прямо пропорциональная (линейная зависимость). Это положение носит название Закон Гука: () Коэффициент пропорциональности Е называют модулем упругости. Очевидно, Е имеет ту же размерность, что и напряжение, т.е. выражается в Па или МПа.
Диаграмма растяжения низкоуглеродистой стали.
Условие прочности при растяжении и сжатии.
- Условие прочности при растяжение и сжатии.
-Расчетное нормальное напряжение. - Продольная сила. - Площадь поперечного сечения.
- Допускаемая нагрузка.
1.
Условие прочности при смятии.
- Условие прочности при смятии.
- расчетное напряжение смятия. - Сила сжатия. - Площадь, на которой происходит смятие.
1. 2.
Условие прочности при сдвиге и срезе. Закон Гука при сдвиге.
- Условие прочности при сдвиге и срезе Па, МПа.
- Расчетное касательное напряжение среза. Па, МПа - Поперечная сила Н. - Площадь среза. - Допустимое. - Площадь среза. - Допустимое касательное напряжение среза Па, МПа.
1. - проектный расчет определяемой площади.
2.
Закон Гука при чистом сдвиге. Расчетное касательно напряжение прямопропорционально углу сдвига, где коэффициент пропорционален. () G – Модуль упругости 2 рода жесткости материала или модуль сдвига. Па, МПа. На кручении рассчитывают валы, которые передают мощность.
1.
2.
Закон Гука при чистом сдвиге. Расчетное касательное напряжение прямопропорционально углу сдвига, где коэффициент пропорциональности G.
G – модуль упругости 2 рода, модуль сдвига. Па, МПа.
Геометрические характеристики плоских сечений. 1. - Площадь круга.
- Площадь кольца.
d – наружный диаметр. d0 – внутренний диаметр. 2. Wp – полярный момент сопротивления. а) б)
3. Ip – полярный момент инерции. а) б)
4. Wx – осевой момент сопротивления. а) б)
|
||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 81; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.1.63 (0.005 с.) |

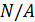 , где Ƈ(сигма)
, где Ƈ(сигма)
 - условие прочности при смятии.
- условие прочности при смятии.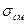 - расчетное напряжение смятия, Па, МПа
- расчетное напряжение смятия, Па, МПа - сила сжимающая, Н, кН
- сила сжимающая, Н, кН - площадь, на которой происходит смятие, мм2, м2
- площадь, на которой происходит смятие, мм2, м2 2.
2. 
 - условие прочности при сдвиге или срезе (проверочный расчет)
- условие прочности при сдвиге или срезе (проверочный расчет)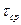 - расчетное касательное напряжение среза. Па, МПа
- расчетное касательное напряжение среза. Па, МПа - поперечная сила, Н.
- поперечная сила, Н. - площадь среза, м2, мм2, см2.
- площадь среза, м2, мм2, см2. - допустимое касательное напряжение среза Па, МПа.
- допустимое касательное напряжение среза Па, МПа.
 - проектный расчет определение площади среза.
- проектный расчет определение площади среза.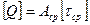 - расчет на допустимую нагрузку, Н, кН.
- расчет на допустимую нагрузку, Н, кН.



