
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статическая характеристика регулятораСодержание книги
Поиск на нашем сайте
Статическая характеристика регулятора описывается уравнением: Y= Подставить вместо Nсвой порядковый номер. (1) Y= Для построения характеристики определим точки где X1=0, X2=2: Y1= Y2= По этим точкам построить статическую характеристику регулятора
рисунок 5 (Статическая характеристика регулятора)
Статическая характеристика исполнительного механизма Статическая характеристика исполнительного механизма описывается уравнением: Y=X/ Подставить вместо Nсвой порядковый номер. (1) Y=X/ Для построения статической характеристики исполнительного механизма задаться точками X1=0, X2=2: Y1=0/ Y2=2/ По этим точкам построить статическую характеристику исполнительного механизма
рисунок 6 (Статическая характеристика исполнительного механизма) Раздел 7 Статические характеристики системы. Рабочая точка. Динамический коэффициент регулирования Общая статическая характеристика Определить общую статическую характеристику цепи обратной связи (ДРИМ), изобразить статические характеристики этих звеньев на общей плоскости. В первом квадрате расположить статическую характеристику датчика, во втором - статическую характеристику регулятора, в третьем – статическую характеристику исполнительного механизма. Для определения результирующей статической характеристики разбить ось хд на равные отрезки. Из точек 1 и 2 провести перпендикуляры до пересечения с линейной статической характеристикой датчика. Получить точки A1 и В1. Из этих точек провести горизонтали до пересечения с линейной статической характеристикой регулятора. Получить точки А2 и В2. Из этих точек опустить перпендикуляры. Горизонтальное положение оси Хр поменять на вертикальное. Из новых точек А2 и В2 провести горизонтали до пересечения с соответствующими перпендикулярами в точках A3 и В3. Соединить эти точки и получить результирующую статическую характеристику обратной связи.
Рабочая точка и угол между характеристиками Определить взаимосвязь между статическими характеристиками объекта и обратной связью. Изобразить характеристики в одной системе координат.
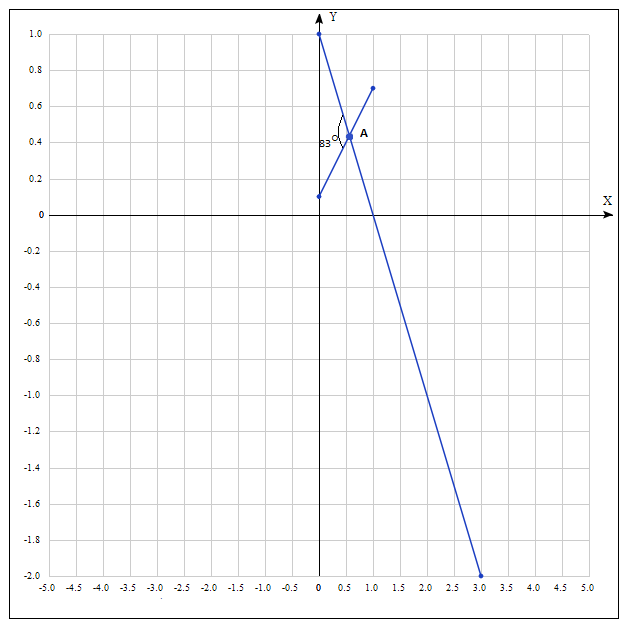
рисунок 7 (График статических характеристик системы)
Статические характеристики объекта и обратной связи пересекаются в точке А. Эта точка, называется рабочей точкой. Угол пересечения двух статических характеристик равен 83°. Устойчивость системы считается хорошей, если статические характеристики пересекаются под углом от 60° до 90°. Если система не обладает достаточной устойчивостью, то в цепь обратной связи включают усиливающее или ослабляющее звенья, что приведет к согласованности масштабов по осям. В данном случае коррекция не требуется, так как угол пересечения двух статических характеристик находится в пределах от 60° до 90°. Угол пересечения статических характеристик равен 83°.
Динамический коэффициент регулирования Рассчитать динамический коэффициент регулирования. Для этого рассмотреть предыдущий рисунок (рисунок 7). На этом рисунке по одной характеристике определяется возможный диапазон измерений входного параметра. Произвести фиксацию двух точек возможного диапазона измерений, затем, эти две точки перенести на вторую статическую характеристику и с помощью этой характеристики определить диапазон изменения выходного параметра. В результате по статической характеристике обратной связи получим:
По статической характеристике объекта получаем: ∆ Y= 0.7 Подставим эти значения ∆X и ∆Y в выражение: Д = ∆Y/∆Xвх =0.7/1=0.7 При Д=1 система имеет оптимальную передачу сигнала в замкнутом контуре. При Д> 1 в систему обратной связи следует включить ослабитель сигнала. При Д< 1 в цепь обратной связи следует включить усилитель сигнала. Так как необходим динамический коэффициент, равный единице, то в цепь обратной связи включен усилительный элемент с коэффициентом передачи к = 1,5 Координаты рабочей точки Определить координаты рабочей точки.
Для определения координат рабочей точки системы привести структурную схему в виде двух элементов, с целью определения взаимосвязи регулирующих параметров. Поскольку статические характеристики представляются прямыми линиями, то необходимо найти точку пересечения двух прямых. Эти прямые задаются уравнениями устойчивости из представленных расчетов:
Вместо N подставить свой порядковый номер (1).
Координаты рабочей точки:
-2X=0,7-1 X=(0,7-1)/2 X=0,15 Y=1+0,15 Y=1,15 A(-0,15;1,15)
Раздел 8 Преобразование статических характеристик Определить аналитическое выражение режима работы регулирующей системы, осуществив преобразование статических характеристик датчика, регулятора и исполнительного механизма: уравнение для объекта регулирования:Y=N-X уравнение для датчика: Y= уравнение для регулятора: Y= уравнение для исполнительного механизма: Y=X/ Из структурной схемы следует, что Yд =Xр ; Yр = Xи.м. Подставить уравнение датчика в уравнение регулятора. Результирующее уравнение подставить в уравнение для исполнительного механизма. Yp= В уравнение для регулятора подставить вместо N свой порядковый номер. (1) Yp= Упростить выражение, подставив вместо N свой порядковый номер. (1). Yp= Подставить значение выражения в уравнение исполнительного механизма: Yи.м=Yp/ Полученное выражение является статической характеристикой цепи обратной связи, полученной аналитическим способом. Оно также описывает статическую характеристику цепи обратной связи, полученную ранее графическим способом.
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 284; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.88.8 (0.009 с.) |

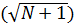 – X/N
– X/N – X/1
– X/1

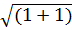


 ∆ Xвх =1
∆ Xвх =1



 ) - X/N
) - X/N


