
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение степени статической неопределимости или числа лишних связей nСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
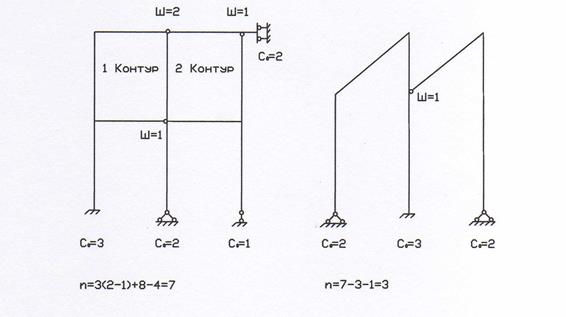
Для многоэтажных рам с наличием замкнутых (непрерывных) контуров можно воспользоваться следующей формулой n = 3 (К – 1) + где К– число замкнутых контуров; Ш =С -1, здесь С – число стержней, соединенных шарниром в одном узле (рис. 1).
Рис. 1
Для простых рам проще определять степень статической неопределимости по формуле: n = На рис. 2 показаны примеры вычисления n по (8) и (9).
а) б)
Рис. 2
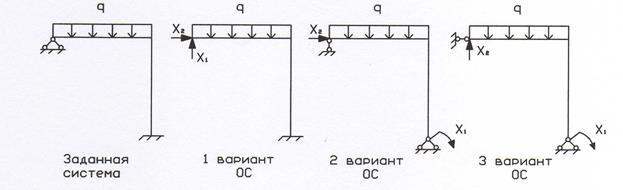
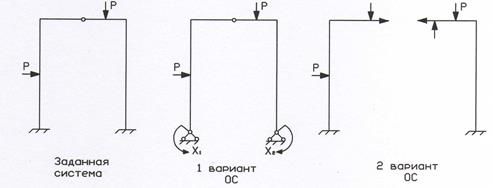
Выбор основной системы ОС Основная система метода сил получается из заданной путем отбрасывания n лишних связей и заменой их неизвестными реакциями, действующими по направлению отброшенных связей. ОС должна быть статически определимой и геометрически неизменяемой (т.е. не должна менять свою геометрию без деформаций элементов). Вариантов ОС может быть несколько. Это зависит от выбора отброшенных связей, причем, отбрасываться могут как внешние связи (рис. 3 а), так и внутренние (рис. 3 б, 2 вариант). В работе предлагается выбрать три варианта ОС, а затем принять из них за расчетный наиболее простой для построения эпюр моментов (вариант 1).
а)
б)
Рис. 3
Составление системы канонических уравнений метода сил (СКУ)
Для определения неизвестных сил Для рамы, дважды статически неопределимой, СКУ имеет вид:
4. Построение единичных эпюр моментов
Единичные эпюры моментов
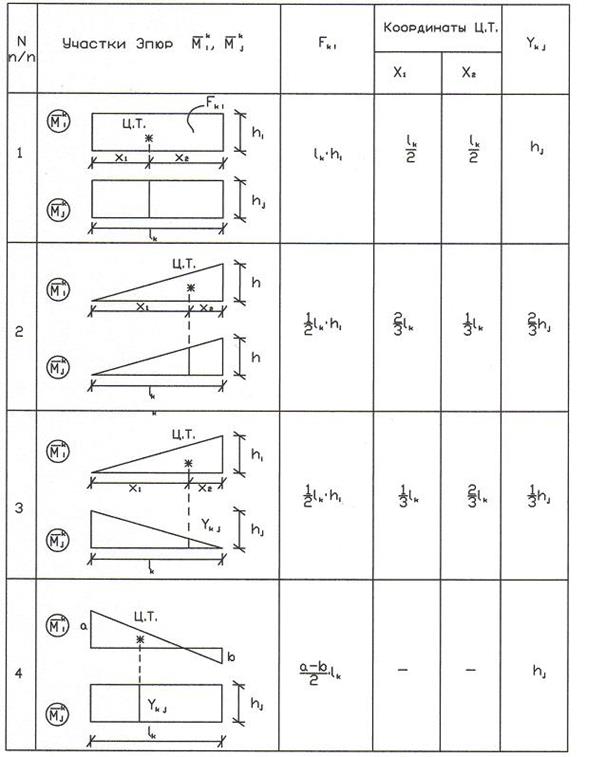
Рис. 4 Определение главных и побочных коэффициентов СКУ Так как по физическому смыслу жесткостей EI. Важно правильно применять каждую из формул. Например, формулой Верещагина удобно пользоваться тогда, когда перемножаемые эпюры на участках линейны и имеют вид фигур, для которых легко определить центр тяжести «Ц.Т.» (прямоугольника, треугольника). По способу Верещагина
где Таблица
Правило знаков: в формуле (10) ставится знак плюс, когда эпюры В качестве примера для рамы, изображенной на рис. 4, вычислим с помощью формулы Верещагина главные коэффициенты СКУ:
По теореме о взаимности перемещений побочные коэффициенты СКУ равны между собой:
Формулу Симпсона используют тогда, когда одна из перемножаемых эпюр криволинейна. В этом случае:
Входящие в формулу величины показаны на рис. 5. Каждое слагаемое в скобках берется со знаком плюс, если соответствующие ординаты расположены по одну сторону от оси, и со знаком минус, если с разных сторон.
Рис. 5 Если обе эпюры моментов прямолинейны, то формула Симпсона приводится к формуле трапеций:
= ±
Проверка главных и побочных коэффициентов СКУ Проверка главных и побочных коэффициентов производится с помощью универсального равенства (4). Если оно не выполняется, то для уточнения, в каком перемещении допущена ошибка, делаются построчные проверки каждого канонического уравнения:
|
||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 786; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.191.241 (0.009 с.) |

 - Ш, (8)
- Ш, (8)
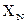 составляются дополнительные уравнения совместности деформаций, физический смысл которых заключается в эквивалентности перемещений заданной системы и перемещений в ОС от внешней нагрузки и сил
составляются дополнительные уравнения совместности деформаций, физический смысл которых заключается в эквивалентности перемещений заданной системы и перемещений в ОС от внешней нагрузки и сил 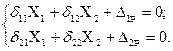
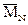
 строятся в ОС от последовательного приложения сил
строятся в ОС от последовательного приложения сил  = 1,
= 1, 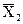 = 1,...,
= 1,...,  =1 без учета внешней нагрузки по правилам сопромата для статически определимых рам. В качестве примера на рис. 4 изображены эпюры
=1 без учета внешней нагрузки по правилам сопромата для статически определимых рам. В качестве примера на рис. 4 изображены эпюры  и
и 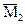 . Знак на эпюрах моментов не ставится, они всегда строятся со стороны растянутого волокна.
. Знак на эпюрах моментов не ставится, они всегда строятся со стороны растянутого волокна.
 являются перемещениями, то их можно вычислить по формуле Мора (2) с помощью формулы Верещагина, Симпсона, трапеций. Предварительно единичные эпюры моментов разбиваются на участки интегрирования не только по узловым точкам, но и по точкам изменения характера нагрузки и точкам изменения
являются перемещениями, то их можно вычислить по формуле Мора (2) с помощью формулы Верещагина, Симпсона, трапеций. Предварительно единичные эпюры моментов разбиваются на участки интегрирования не только по узловым точкам, но и по точкам изменения характера нагрузки и точкам изменения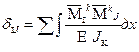 = ±
= ± 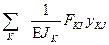 = ±
= ±  , (10)
, (10)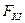 ,
, 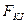 – площади эпюры
– площади эпюры 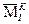 или
или  на k–м участке;
на k–м участке;  ,
, 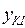 –ординаты с эпюры
–ординаты с эпюры 
 =
= 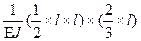 +
+ 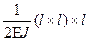 =
= 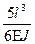 ;
;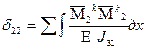 =
= 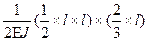 =
= 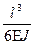 .
.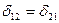 =
= 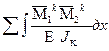 =
= 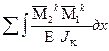 =
= 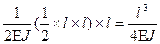 .
.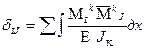 = ±
= ± 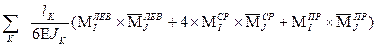 . (11)
. (11)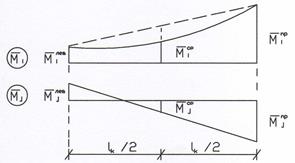
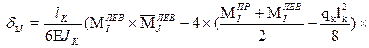
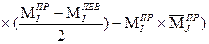 .
.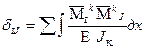 =
=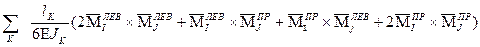 . (12)
. (12)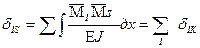 . (13)
. (13)


