
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение грузовой эпюры моментовСодержание книги Поиск на нашем сайте
Эпюра
Рис. 6
Определение грузовых коэффициентов СКУ Грузовые коэффициенты определяются также с помощью интеграла Мора по формуле (3):
Перемножение единичных эпюр моментов
Проверка грузовых коэффициентов СКУ Грузовые перемещения проверяются путем перемножения суммарной единичной
В противном случае следует дополнительно проверить построение грузовой эпюры моментов.
Решение системы канонических уравнений
Найденные в п. 5 и п. 8. коэффициенты подставляем в СКУ (1) и решаем ее любым известным способом решения системы линейных алгебраических уравнений. Например, способом Гаусса, способом последовательных приближений, матричным способом и другими. Определив корни системы уравнений (1), необходимо их проверить подстановкой в исходные уравнения и вычислить погрешность решения, которая не должна превышать 2%. Погрешность вычислений можно определить по формуле:
где П–сумма положительных слагаемых равенства; О–сумма отрицательных слагаемых равенства; М–минимальное число из «П» и «О». Например, погрешность вычисления 42-45-79+80=0 будет равна: П=42+80=122; О=45+79=124; М=122; В результате решения СКУ получаем значения неизвестных усилий
Построение расчетной эпюры изгибающих моментов Окончательную эпюру моментов
Для полученной эпюры делают узловую проверку. Для этого вырезают узлы рамы, прикладывают к ним заданные моменты, изгибающие моменты с эпюры
12. Деформационная проверка эпюры
Прежде чем произвести деформационную проверку расчетной эпюры моментов выбирается другой вариант основной системы, отличный от принятого для расчета. Для него строится новая суммарная единичная эпюра моментов
Если это условие не выполняется (погрешность вычислений должна быть не более 2%), то дальнейшее решение не имеет смысла. Нужно еще раз проверить выполнение п. 12 и п. 11. Построение расчетной эпюры поперечных сил Эпюра Если на участке не действует распределенная нагрузка (эпюра
где Правило знаков: если ось стержня нужно повернуть по часовой стрелке до совмещения с касательной к эпюре Если на участке действует распределенная нагрузка (эпюра алгоритму: 1. Рассматриваемый участок представляют как простую балку. 2. Считают реакции в опорах этой балки от распределенной нагрузки. 3. В крайнее левое и правое сечения прикладывают моменты, взятые с соответствующего участка эпюры Мрас, и определяют реакции в опорах балки от общего внешнего момента. Знаки для 4. Складывают полученные реакции и строят по ним эпюру Иллюстрация рассмотренного алгоритма показана на рис. 8.
Рис. 7
Рис. 8
|
||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 3425; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.140.78 (0.006 с.) |

 строится в основной системе от действия только заданной нагрузки по правилам сопромата для статически определимых рам. Построим грузовую эпюру моментов для рамы, изображенной на рис. 4 (рис. 6).
строится в основной системе от действия только заданной нагрузки по правилам сопромата для статически определимых рам. Построим грузовую эпюру моментов для рамы, изображенной на рис. 4 (рис. 6).
 .
.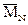 с грузовой
с грузовой  и грузовой
и грузовой  .
. ,
,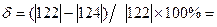 1.639%.
1.639%.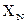 в лишних отброшенных связях.
в лишних отброшенных связях. от заданной внешней нагрузки можно построить по формуле (6). При этом все ординаты единичных эпюр умножаются на соответствующие значения
от заданной внешней нагрузки можно построить по формуле (6). При этом все ординаты единичных эпюр умножаются на соответствующие значения 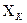 и складываются с ординатами эпюры от внешней нагрузки. Если значения
и складываются с ординатами эпюры от внешней нагрузки. Если значения 
 . (14)
. (14) .
. . Вычисленные по формуле (7) обобщенные перемещения по направлению отброшенных связей должны быть примерно равны нулю:
. Вычисленные по формуле (7) обобщенные перемещения по направлению отброшенных связей должны быть примерно равны нулю: .
.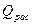 строится по расчетной эпюре моментов по участкам.
строится по расчетной эпюре моментов по участкам.
 , (15)
, (15) – разница моментов на краях к-го участка Мрас;
– разница моментов на краях к-го участка Мрас;  – длина участка.
– длина участка. ;
; 

 ;
; 
 ;
; 

 ;
;



