
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение плотности твердого телаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ПРАКТИЧЕСКИЕ И ЛАБОРАТОРНЫЕ ЗАНЯТИЯ ПО ФИЗИКЕ
Учебное пособие для студентов первого курса медицинских вузов
Пермь 2008 Авторы-составители: Кирко Г.Е.- д-р физ.-мат. наук, проф., Афанасьев А.Л.- канд.биол. наук, Кустова Я.Р., Корякина А.Г., Смирнова З.А., Зернина Н.В., Сазонова Н.К., Черемных М.Р.
УДК 53(076.5) ББК 22.3я73 П 69 ПРАКТИЧЕСКИЕ И ЛАБОРАТОРНЫЕ ЗАНЯТИЯ ПО ФИЗИКЕ: учебное пособие для студентов первого курса медицинских вузов/ Г.Е. Кирко и др./ Пермь: ГОУ ВПО ПГМА им. ак. Е.А. Вагнера Росздрава, 2008-153с.
Представлен курс лабораторных работ по медицинской и биологической физике, включающий в себя необходимый теоретический материал и алгоритм проведения практической работы. Издание иллюстрировано схемами и таблицами для успешного проведения лабораторного практикума. Пособие предназначено для студентов первого курса лечебного, педиатрического, стоматологического и медико-профилактического факультетов медицинских вузов.
ISBN Рецензенты:
Путин Г.Ф. - д-р физ.-мат. наук, профессор Пермского государственного университета, Кузнецов В.А. - д-р физ.-мат. наук, профессор Магнитогорского государственного университета.
Печатается по решению ученого совета ГОУ ВПО ПГМА им. ак. Е.А. Вагнера Росздрава.
УДК 53(076.5) ББК 22.3я73
ISBN ©ГОУ ВПО ПГМА им. ак. Е.А. Вагнера Росздрава, 2008 © Коллектив авторов, 2008
СОДЕРЖАНИЕ
Лабораторная работа №1
ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ ТВЕРДОГО ТЕЛА
Цель работы: освоить расчет ошибок косвенных измерений на примере определения плотности тела. Приборы и принадлежности: цилиндр, технические весы, разновесы, штангенциркуль
ТЕОРИЯ Выполнение лабораторных работ связано с измерением различного рода физических величин. Измерение - это процесс сравнения измеряемой величины с однородной ей величиной, принятой за единицу меры. Вследствие несовершенства наших органов чувств и измерительных приборов измерения выполняются с ограниченной степенью точности, т. е. значение измеряемой величины отличается от истинного. Под степенью точности прибора понимается та наименьшая часть единицы меры, до которой с уверенностью в правильности результата может быть проведено измерение (например, степень точности школьной линейки 1 мм). Ошибки (погрешности), возникающие при измерении, делятся на два больших класса: систематические и случайные. Систематические ошибки - ошибки, сохраняющие свою величину и знак от измерения к измерению. Они связаны с неисправностью прибора, неудачно выбранным методом измерений и т. д. Так как систематические ошибки постоянны, они не поддаются математическому анализу, но их можно выявить и устранить. Случайные ошибки - ошибки, которые непредсказуемым образом изменяют свою величину (и знак) от измерения к измерению. Они являются следствием несовершенства наших органов чувств, действия факторов, влияние которых невозможно учесть, и т. д. Устранить их нельзя, но они подчиняются статистическим закономерностям, их можно рассчитать, используя методы математической статистики. Величина случайной ошибки существенно уменьшается при увеличении числа измерений. Измерения делятся на два вида: прямые и косвенные. Прямые измерения - измерения, при которых числовые значения искомой величины получаются непосредственным сравнением ее с единицей меры. Косвенные измерения - измерения, при которых значения искомой величины находятся по результатам измерений других величин, связанных с этой величиной, определенной функциональной зависимостью. Лабораторная работа №2 ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛА Цель работы: изучить законы вращательного и колебательного движений и освоить метод определения момента инерции тела. Приборы и принадлежности: физический маятник, секундомер, измерительная линейка.
ТЕОРИЯ
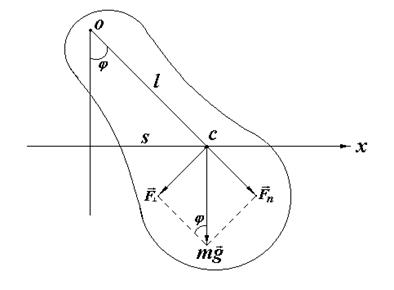
Физический маятник – твердое тело произвольной формы, произвольных размеров, способное колебаться относительно горизонтальной оси, не проходящей через центр масс (рис.1).
О - точка, через которую проходит ось вращения; С - центр масс; l = ОС – приведённая длина маятника; S – смещение центра масс от положения равновесия; φ - угол отклонения маятника от положения равновесия. При выведении из положения равновесия физический маятник колеблется относительно оси, проходящей через точку О. При отклонении маятника от положения равновесия на угол Знак «-» показывает, что сила направлена к положению равновесия (против смещения). При малых углах отклонения траекторию движения точки можно считать прямой линией, совпадающей с осью абсцисс. Если угол Получим закон движения маятника. Из рисунка 1 видно, что М = - mgl Основной закон динамики вращательного движения можно записать в виде М = I где Сравнивая (1) и (2), получим
или Разделив обе части выражения (3) на I, имеем
Выражение (4) является дифференциальным уравнением движения физического маятника. Произведя замену
Она связана с периодом колебаний Т соотношением Тогда
Зная период колебаний Т, можно рассчитать момент инерции I физического маятника. ОПИСАНИЕ УСТАНОВКИ
Физический маятник (рис.2) состоит из металлического тела прямоугольной формы с вырезами. Осью вращения служит ребро призмы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Закрепить маятник на стержне. Определить t - время 20-30 полных колебаний (N). Опыт повторить 5 раз. Результаты измерений занести в таблицу. 2. Измерить линейкой расстояние l от центра масс до точки подвеса (рис.2). Опыт повторить 5 раз. Результаты измерений занести в таблицу.
3. Найти среднее значение измеренных величин как среднее арифметическое:
4. Выразить среднее значение периода через
Найти среднее значение момента инерции физического маятника:
где m – масса маятника (указана на установке).
5. Найти относительную погрешность:
ПРИМЕЧАНИЕ: в данной работе а) Вычислить суммарную ошибку
здесь Значения
б) Аналогично найти суммарную ошибку
где
в) Вычислить относительную погрешность
6. Найти абсолютную погрешность момента инерции:
7. Записать окончательный результат в виде
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Записать формулу связи между линейным и угловым путём, который проходит точка, движущаяся по окружности радиусом R. 2. Как связаны между собой линейная скорость V и угловая скорость 3. Как связаны между собой тангенциальное ускорение 4. Основной закон динамики вращательного движения. Две формулы. 5. Как рассчитать момент силы М (по определению)? Единицы измерения. 6. Как рассчитать момент инерции I материальной точки массой m относительно оси, находящейся от неё на расстоянии r? Единицы измерения. 7. Что называется периодом колебаний Т? Единицы измерения.
Лабораторная работа №3 ИЗУЧЕНИЕ УПРУГИХ СВОЙСТВ КОСТНОЙ ТКАНИ
Цель работы: Рассчитать модуль упругости костной ткани и сравнить его с модулем упругости стали. Приборы и принадлежности: установка для изучения упругих свойств материалов, пластина костной ткани, стальная пластина, набор грузов, линейка, микрометр. ТЕОРИЯ Механические свойства твердых тел В настоящее время на стыке механики, математики и ряда биологических и медицинских наук развилось новое научное направление – биомеханика. Её основная задача состоит в изучении закономерностей движения и деформирования различных биологических тканей под воздействием внешней среды. Изучение механических свойств биологических тканей позволяет создавать новые схемы армирования конструкционных материалов и эффективные структуры синтетических материалов, применяемых для замещения пораженных тканей. В некоторых разделах медицины, особенно в хирургии и ортопедии, при изучении опорно-двигательного аппарата человека очень важным является знание упругих свойств тканей организма, в частности костной ткани. Рассмотрим механические свойства твердых тел, так как костная ткань относится к твердым телам. Все тела деформируются под действием сил. Деформацией называют изменение формы и объёма тела, происходящее под действием внешних сил. Различают деформации упругие и пластические (остаточные). Упругой называют деформацию, которая при прекращении действия внешних сил полностью исчезает, тело восстанавливает свои размеры и форму. Пластической называют деформацию, которая сохраняется и после прекращения действия внешних сил. Является деформация упругой или пластической –зависит от материала тела и от величины приложенных к телу сил. Упругие деформации подчиняются закону Гука. Гук установил связь между величиной деформации и силами, её обусловливающими. Согласно закону Гука при упругой деформации деформирующая сила F и величина деформации x пропорциональны между собой: F = - k x.
Различают пять основных видов деформации: - растяжение, - сжатие, - кручение, - сдвиг, - изгиб.
В конечном счете любую деформацию можно свести к двум наиболее простым: растяжению и сдвигу. При деформации твердых кристаллических тел частицы, находящиеся в узлах кристаллической решетки, смещаются в новые положения. Этим смещениям препятствуют силы взаимодействия между частицами, поэтому в деформируемом теле возникают внутренние упругие силы F упр. Эти силы уравновешивают внешние силы F вн, приложенные к телу. F упр =F вн. Таким образом, при деформации в теле возникает особое напряжённое состояние. Количественно это состояние характеризуют механическим напряжением s. Механическим напряжением называют физическую величину, численно равную упругой силе, приходящейся на единицу площади поперечного сечения тела:
Мерой деформации служит относительная деформация e:
где x – первоначальный размер тела, D x – изменение этого размера (например, l – длина, D l – удлинение). Опыт показывает, что механическое напряжение s пропорционально относительной деформации e, если деформация упругая:
Модуль Юнга численно равен напряжению, при котором относительная деформация равна единице (т.е. удлинение D l равно первоначальной длине l). На самом деле столь большие упругие деформации невозможны, т.к. при значительно меньших напряжениях происходит разрыв тела. График зависимости s= f(x) изображён на рис. 1
Рис. 1 В области ОА справедлив закон Гука, сохраняется пропорциональность относительной деформации и механического напряжения. Точка А соответствует пределу пропорциональности. Точка В соответствует пределу упругости sупр. Пределом упругости sупр называют наибольшее напряжение, при котором деформация еще сохраняет упругий характер. Материалы с высоким пределом упругости называют упругими. Горизонтальный участок кривой определяет текучесть – такое состояние деформированного тела, при котором деформация возрастает без увеличения напряжения. Свойство материалов выдерживать действие внешних сил без разрушения называют прочностью. Точка D на кривой соответствует пределу прочности. Пределом прочности sпр называют механическое напряжение, которое соответствует наибольшей выдерживаемой телом нагрузке перед разрушением. Обычно для кристаллических тел этот график одинаков для растяжения и сжатия. Однако сложные по составу или неоднородные материалы (например, дерево, бетон, кость, пластмассы) проявляют различные свойства при растяжении и сжатии. Модуль Юнга, предел упругости и предел прочности у таких материалов будут различными для разных видов деформации. Между упругими свойствами кристаллических мономеров и полимерных материалов существует принципиальная разница. Это связано с другим механизмом упругости высокомолекулярных соединений. Рассмотрим механизм упругости кристаллических твердых тел и полимеров. В основе деформации кристаллических тел лежит искажение пространственной решетки. При упругой деформации происходит только небольшое смещение частиц, образующих решетку. При этом нарушается равновесное соотношение между силами притяжения и отталкивания. В связи с этим возникают внутренние силы, противодействующие внешним. Эти силы восстанавливают первоначальную форму тела при прекращении действия внешних сил. При остаточной деформации искажение решётки настолько значительно, что прежние связи между частицами нарушаются и устанавливаются новые равновесные связи. Упругость полимеров называют каучукоподобной эластичностью (или высокоэластичностью). Эластичными называют материалы, способные к большим упругим деформациям. Особенность упругих свойств полимеров обусловлена их строением. Полимерами называют вещества, молекулы которых представляют собой длинные цепи, составленные из большого числа атомных группировок, соединенных химическими связями. Молекулы полимеров причудливо изогнуты, их форма и размеры все время меняются в результате теплового движения. При наложении механической нагрузки молекулы полимера вытягиваются в соответствующем направлении и размеры тела увеличиваются. После снятия нагрузки молекулы, вследствие теплового движения, восстанавливают свои размеры. Деформация полимера упругая, остаточные деформации у большинства полимеров практически отсутствуют. Механические свойства полимера являются сочетанием свойств твердых тел и жидкостей. Полимеры достаточно прочны и способны к большим упругим деформациям. К полимерам можно отнести кожу, волосы, рога, шерсть, шелк, хлопок и т.д. Биополимеры являются структурной основой всех живых организмов и играют большую роль в процессе их жизнедеятельности. К биополимерам относятся белки, нуклеиновые кислоты, полисахариды, гликопротеиды, гликолипиды и др. Из множества биологических тканей наибольший интерес для механики представляет компактная костная ткань. Она является основным составным веществом длинных трубчатых костей, воспринимающих механические нагрузки.
Механические свойства костной ткани Кость – основной материал опорно-двигательного аппарата. Костная ткань представляет собой форму соединительной ткани. Она является живой тканью, в которой происходит постоянное внутреннее разрушение и обновление биохимических компонентов. Строение костной ткани достаточно сложно. Вещество костной ткани состоит из органических волокон коллагена, неорганических кристаллов и связующего вещества. Связующее (цементирующее) вещество состоит в основном из мукополисахаридов. Неорганическое вещество кости – это различные соли кальция. Кристаллы неорганических веществ в кости образуют сложный минерал, принадлежащий к классу апатитов. Свежая костная ткань содержит 60% Ca3(PO4)2, 5,9% CaCO3 и 1,4% Mg(PO4)2. В упрощенном виде можно считать, что 2/3 массы компактной костной ткани составляет неорганический материал, минеральное вещество кости – гидроксилапатит, представляющее собой микроскопические кристаллики. В остальном кость состоит из органического материала, главным образом коллагена (высокомолекулярного соединения), обладающего высокой эластичностью. Интересно отметить некоторую особенность костной ткани. Если из неё удалить неорганические вещества, то оставшиеся органические компоненты внешне сохраняют форму кости, но механические свойства нового материала становятся резиноподобными. Если же из костной ткани удалить органические вещества, то внешняя форма кости тоже сохраняется, но материал становится хрупким, с низкой механической прочностью. Это значит, что ни органические, ни неорганические составляющие не являются по отдельности прочным конструкционным материалом для костной ткани. Костная ткань образуется только определенным сочетанием компонентов и обладает прочностью, сравнимой с металлами. Сложное строение костной ткани придает ей нужные механические свойства: твердость, прочность, упругость. Механические свойства кости зависят от многих факторов, в том числе от возраста, индивидуальных условий роста организма, участка организма, питания и др. Зависимость механического напряжения от относительной деформации для компактной костной ткани показана на рис. 2.
Из рисунка видно, что данная зависимость подобна аналогичной зависимости для твердого тела. При малых деформациях выполняется закон Гука. Модуль Юнга у костной ткани приблизительно равен 1010 Па, а предел прочности - 108 Па. На практике модуль Юнга чаще измеряют в кГ/мм2. ü Для костной ткани он колеблется в пределах от 1600 кГ/мм2 до 2000 кГ/мм2 в зависимости от участка тела и условий жизни человека. ü Для сравнения: модуль Юнга стали равен 20000 кГ/мм2. Известно, что после длительного действия механических нагрузок костная ткань не восстанавливает полностью своих прежних размеров, т.е. сохраняется некоторая остаточная деформация. Это свойство костной ткани используется в ортопедии.
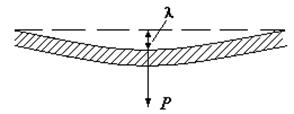
ПРАКТИЧЕСКАЯ ЧАСТЬ Методы определения механических свойств у биологических тканей аналогичны методам определения этих свойств у технических материалов. При экспериментальных исследованиях упругих свойств костной ткани будем считать, что кость имеет сплошное строение, однородна и изотропна, т.е. обладает одинаковыми механическими свойствами по всем направлениям. Существуют различные способы определения модуля упругости твердых тел. В данной работе модуль упругости определяется по деформации изгиба. Если прямую упругую пластину свободно положить на твердые опоры и нагрузить посредине грузом Р, то пластина изогнется (рис. 3).
При таком изгибе верхние слои пластины будут испытывать сжатие, а нижние – растяжение. Слой же, расположенный посредине, не испытывает ни растяжения, ни сжатия. Этот слой называют нейтральным, он сохранит свою длину и только прогнется. Перемещение l, которое получает середина пластины, называют стрелой прогиба. Она тем больше, чем больше нагрузка, и зависит от модуля упругости материала. В теории сопротивления материалов доказано, что стрела прогиба находится по формуле
где В – коэффициент, зависящий от размеров тела. Для прямой пластины: где L – длина, a – ширина, b – толщина пластины. Подставив это выражение в формулу для стрелы прогиба, получим
Отсюда модуль упругости рассчитывается по формуле
Интересно отметить, что сопротивление изгибу оказывают только те слои, которые растягиваются или сжимаются. Чем ближе к нейтральному слою расположен слой, тем меньшее сопротивление он оказывает. Нейтральный слой сопротивления почти не оказывает. Поэтому если внутренние слои образца будут отсутствовать, то его сопротивление изгибу почти не изменится, но вес образца уменьшится значительно. С точки зрения экономии материала и уменьшения веса выгодно использовать полые стержни (трубки). Это широко используется в технике. Трубчатую форму имеют и многие кости человека, животных, птиц. Трубчатыми являются также стебли некоторых растений. Однако нельзя сколь угодно уменьшать толщину, так как тонкие трубки оказывают малое сопротивление изгибу. Должно соблюдаться вполне определенное соотношение внешнего и внутреннего диаметров трубы. ОПИСАНИЕ УСТАНОВКИ Установка для определения модуля упругости состоит из платформы 1, на которой находится опора 2 для образца 8 (рис. 4).
По краям опоры на стойках с помощью специальных винтов 3 закреплена планка 4, в которую вмонтирован индикатор перемещения 5, измеряющий стрелу прогиба. На верхнем конце упора индикатора 6 находится чашечка 6 для грузов. Регулировка планки по высоте производится с помощью винтов. Планку необходимо устанавливать на такой высоте, чтобы чашечка была приподнята (т.е. не лежала на ободе индикатора). ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Линейкой измерить длину L (длина L - расстояние между внутренними краями опоры, так как только эта часть образца испытывает деформацию изгиба). Результат измерений записать в табл. 1. 2. С помощью микрометра измерить ширину a образца костной ткани. Результаты записать в табл. 1. 3. Микрометром измерить толщину образца b 5 раз и записать в табл. 1. Таблица 1
4. Положить образец на опору и подвести нижний конец упора индикатора к центру образца. 5. Поворотом шкалы совместить нуль индикатора со стрелкой. 6. Положить груз в чашечку на индикатор и измерить стрелу прогиба 7. Проделать аналогичные измерения для стального образца. Результаты измерений записать в табл. 2. Таблица 2
8. Вычислить средние значения 9. Рассчитать средние значения модуля упругости для костной ткани и стали по формуле
10. Найти абсолютные погрешности отдельных измерений ширины, толщины и стрелы прогиба. 11. Найти погрешность D L по формуле 12. Вычислить суммарную погрешность D a: D a =
Для рекомендуемой надежности a= 0,95 и числа измерений n = 5 t a ,n = 2,8. Для микрометра и индикатора перемещения Dпр = 0,007 мм, Dокр = 0,005 мм. 13. Аналогично рассчитать суммарные ошибки D b и Dl. 14. Вычислить относительную погрешность
15. Найти абсолютную погрешность измерения модуля упругости:
16. Записать окончательный результат измерения модуля упругости в виде
17. Сравнить модули упругости костной ткани и стали.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Механические свойства твердых тел. Виды деформаций. 2. Механизм упругости твердых тел и полимеров. 3. Закон Гука. Предел упругости, предел прочности, текучесть. 4. Механическое напряжение, абсолютная и относительная деформация. 5. Модуль Юнга, его физический смысл и единицы измерения. 6. Механические свойства костной ткани. Состав и строение костной ткани. 7. Методика определения модуля Юнга по деформации изгиба. 8. Расчет погрешности измерений по результатам данной лабораторной работы.
Лабораторная работа №4 ГИДРОДИНАМИКИ И РЕОЛОГИИ ТЕОРИЯ Линии и трубки тока. Уравнение неразрывности струи Гидродинамика – раздел гидроаэромеханики, в котором изучается движение несжимаемых жидкостей и их взаимодействие с твердыми телами. В гидродинамике различают понятия идеальной и реальной жидкостей. Идеальной называют воображаемую жидкость, лишенную вязкости и теплопроводности. Для описания движения жидкости используют понятия «линия тока» и «трубка тока». При установившемся течении все частицы жидкости движутся по определенным траекториям с определенными скоростями.
Линия тока – это линия, в каждой точке которой вектор скорости частицы направлен по касательной (рис.1.).
Понятие линии тока позволяет изобразить поток жидкости графически. Условились проводить линии тока так, чтобы густота их была пропорциональна величине скорости в данном месте. Там, где линии проведены гуще, скорость течения больше, и наоборот (рис.2). В общем случае величина и направление вектора Возможно течение, при котором любая частица жидкости проходит данную точку пространства с одной и той же скоростью. Течение принимает стационарный характер. Стационарным называют такое течение, при котором в данной точке вектор скорости
Трубка тока – это объем жидкости, ограниченный линиями тока (рис.3). S 1 и S 2 – два произвольных сечения трубки тока;
сечениях. Рассмотрим сечение S трубки тока, перпендикулярное скорости
За время V = S а за единицу времени объем
Теорема о неразрывности струи: при стационарном течении идеальной жидкости произведение площади поперечного сечения S трубки тока на скорость сечения жидкости V есть величина постоянная для любого сечения трубки тока, т.е.
Для доказательства возьмем трубку тока настолько тонкую, что в каждом сечении скорость можно считать постоянной (рис.5.) Жидкость абсолютно несжимаема, т.е. ее плотность во всем объеме жидкости одинакова и неизменна. Тогда количество жидкости между сечениями S | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

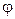 силу тяжести
силу тяжести  можно разложить на составляющие
можно разложить на составляющие  Сила
Сила  создает вращающий момент сил:
создает вращающий момент сил: 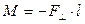 .
.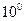 , то
, то 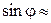
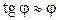 , где
, где  sin
sin 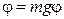 , тогда момент сил
, тогда момент сил , (2)
, (2) угловое ускорение, I - момент инерции маятника.
угловое ускорение, I - момент инерции маятника.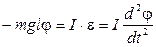
 . (3)
. (3) . (4)
. (4) , получим дифференциальное уравнение гармонического колебательного движения:
, получим дифференциальное уравнение гармонического колебательного движения: , где
, где 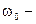 циклическая частота колебания.
циклическая частота колебания.

 отсюда
отсюда . (5)
. (5)



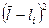
 где n – число измерений.
где n – число измерений.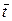 и N:
и N:

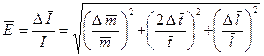
 очень малая величина, поэтому этим отношением можно пренебречь.
очень малая величина, поэтому этим отношением можно пренебречь. :
: ;
;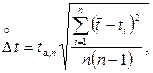 где n =5,
где n =5,  2,8.
2,8. взять из таблицы.
взять из таблицы. :
: ,
, .
.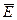 по формуле, приведенной в п.5.
по формуле, приведенной в п.5.

 ?
? .
.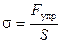 .
.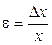 ,
, , где Е – модуль упругости (или модуль Юнга).
, где Е – модуль упругости (или модуль Юнга).

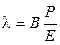 ,
,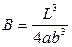 ,
, .
.








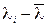

 по красной шкале. Измерения провести 5 раз при одной и той же нагрузке и записать в таблицу.
по красной шкале. Измерения провести 5 раз при одной и той же нагрузке и записать в таблицу. для образцов костной ткани и стали.
для образцов костной ткани и стали.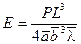 .
. , где для линейки Dпр= 0,7 мм, Dокр= 0,5 мм.
, где для линейки Dпр= 0,7 мм, Dокр= 0,5 мм.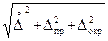 , где
, где  .
. измерения модуля упругости по формуле
измерения модуля упругости по формуле .
. .
. .
.
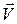 в каждой точке пространства могут изменяться со временем, поэтому и картина линий тока будет меняться.
в каждой точке пространства могут изменяться со временем, поэтому и картина линий тока будет меняться.
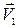 и
и 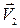 – скорости течения жидкости в этих
– скорости течения жидкости в этих
 t через сечение S пройдут все частицы, расстояние которых от S в начальный момент времени не превышает расстояние l = V
t через сечение S пройдут все частицы, расстояние которых от S в начальный момент времени не превышает расстояние l = V  t. Поэтому за время
t. Поэтому за время 
 . (1)
. (1) 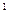
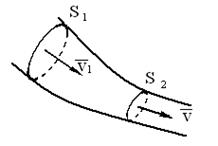
 и S
и S  будет оставаться постоянным, а это возможно только при условии, что объем жидкости, протекающей через сечение S
будет оставаться постоянным, а это возможно только при условии, что объем жидкости, протекающей через сечение S 


