
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Индуктивность в цепи переменного токаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
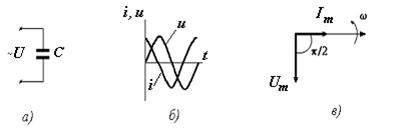
Рассмотрим цепь переменного тока, в которую включена катушка индуктивностью L (Рис.3, а). Пусть напряжение в цепи изменяется по закону u=Um sinw t. При протекании переменного тока через катушку на концах катушки возникает ЭДС самоиндукции ε i = - L Если активное сопротивление катушки принять равным нулю, то внешнее приложенное напряжение U, согласно закону Ома для цепи, содержащей ЭДС, по величине равно и по направлению противоположно ЭДС самоиндукции, то есть U=- ε i = L или Um sinw t = L Интегрируя последнее выражение получим: i = - Тогда по аналогии с законом Ома для участка цепи можно записать, что I m = где величину При оценке фазовых соотношений между током и напряжением на индуктивности видно, что ток в цепи, подобно напряжению, имеет синусоидальный характер, но по фазе отстает на угол p¤ 2, то есть в момент, когда напряжение на катушке достигает максимума, сила тока равна нулю, а в момент, когда напряжение становится равным нулю, сила тока максимальна по модулю. Графики тока и напряжения, а также векторная диаграмма цепи переменного тока, содержащей индуктивность, представлены на рис. 3 (б, в).
Емкость в цепи переменного тока Рассмотрим цепь переменного тока, в которую включен конденсатор С (Рис.4, а).
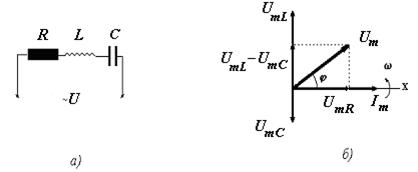
Пусть напряжение в цепи изменяется по закону u = Um sin w t. При напряжении U на конденсаторе емкости С заряд на его обкладках будет равен q=CU. Периодическое изменение U вызывает периодическое изменение q, и возникает емкостный ток: i = Продифференцировав это выражение,получим: i= w CUm cosw t = w CUm sin ( w t + p / 2 ), где w СUm=Im — амплитуда тока. Cравнивая с законом Ома для участка цепи Im=Um/XC, получаем w СUm = Um / XC, отсюда XC = 1 / w C. Видно, что величина XC=1/ w C играет роль сопротивления конденсатора переменному току, она называется емкостным сопротивлением. Из сравнения фазы тока и напряжения видно, что ток в цепи конденсатора, подобно напряжению, имеет синусоидальный характер, но по фазе опережает напряжение на угол p / 2. Цепь переменного тока с активным, индуктивным и емкостным сопротивлениями Рассмотрим основные соотношения электрических величин в цепи переменного тока с индуктивностью, емкостью и активным сопротивлением, соединенными последовательно (рис.5, а).
При последовательном соединении проводников, ток, протекающий через сопротивление одинаков iL=iC=iR=Im sinw t. Полное напряжение цепи будет складываться из падений напряжения на индуктивности, емкости и активном сопротивлении. Составим векторную диаграмму цепи, пользуясь результатами, полученными выше.
В произвольном масштабе отложим вектор амплитуды тока, одинаковый для всех сопротивлений и укажем направление его вращения (Рис. 5, б). Вектор амплитуды напряжения на активном сопротивлении UmR=ImR отложим по направлению вектора тока, так как эти величины совпадают по фазе. Вектор амплитуды напряжения на индуктивном сопротивлении UmL=Im w L отложим вверх под углом p / 2 к вектору тока Im, так как это напряжение опережает ток по фазе на уголp / 2. Вектор амплитуды напряжения на емкости UmC=Im w C отложим вниз под углом p / 2 к вектору Im, так как это напряжение отстает от тока на угол p / 2. Сложив геометрически векторы UmL, UmC и UmR, получим вектор полного напряжения Um, приложенного ко всей цепи (Рис. 5, б).
Применив теорему Пифагора, найдем Um = = Отсюда Im = Последняя формула представляет собой закон Ома для полной цепи переменного тока для амплитудных значений. Полным сопротивлением или импедансом цепи называется величина Z = Закон Ома справедлив и для мгновенных значений тока и напряжения. Угол сдвига фаз между током и напряжением (угол j на рис. 5, б) может быть определен из соотношений tgj =
Импеданс тканей организма Ткани организма представляют собой по электрическим свойствам разнородную среду. Органические вещества (белки, жиры, углеводы и др.), из которых состоят плотные части тканей, являются диэлектриками. Однако все ткани и клетки в организме содержат жидкости или омываются ими (кровь, лимфа, различные тканевые жидкости), в состав этих жидкостей кроме органических коллоидов входят также растворы электролитов, и поэтому они являются хорошими проводниками. Наилучшую электропроводность имеют спинно-мозговая жидкость, сыворотка крови, несколько меньшую - цельная кровь и мышечная ткань. Значительно меньше электропроводность тканей внутренних органов, а также нервной, жировой и соединительной тканей. Плохими проводниками являются роговой слой кожи, связки и сухожилия, костная ткань без надкостницы. В ряде случаев их можно отнести даже к диэлектрикам.
Ткани организма состоят из структурных организмов - клеток, омываемых тканевой жидкостью. Цитоплазма клетки отделена от тканевой жидкости клеточной мембраной. Тканевая жидкость и цитоплазма - хорошие проводники. Клеточная мембрана проводит электрический ток плохо. Такая система напоминает конденсатор и обладает электрической емкостью. В тканях встречаются и макроскопические образования, состоящие из различных соединительных оболочек и перегородок, по обе стороны которых находятся ткани, обильно снабженные тканевой жидкостью. Все это придает тканям емкостные свойства. Как показывает опыт, ткани организма не имеют практически заметной индуктивности, но обладают емкостью и активным сопротивлением. Поэтому при прохождении переменного тока через ткани организма следует учитывать их полное сопротивление, или импеданс. Электрические параметры участка тканей организма, находящиеся между наложенными на поверхность тела электродами, можно представить в виде эквивалентных электрических схем.
В наиболее упрощенном виде эта схема для слоя кожи и подкожной клетчатки может быть представлена как значительная емкость C (Рис.6, а), шунтированная большим сопротивлением R и включенная последовательно со значительно меньшим сопротивлением R *, а для глубоко лежащих тканей - это включенные параллельно сопротивление и емкость (Рис.6, б). Импеданс тканей организма зависит от множества физиологических условий, основным из которых является состояние кровообращения, в частности кровонаполнение сосудов. На этом основан один из способов исследования периферического кровообращения - РЕОГРАФИЯ. При этом в течение цикла сердечной деятельности регистрируется изменение импеданса определенного участка тканей, на границах которого накладываются электроды. При реографии применяется переменный ток частотой 20 - 30 кГц. Этим методом получают реограммы головного мозга - реоэнцефалограммы, печени, легких, магистральных сосудов и т.д. Зависимость импеданса тканей организма от частоты переменного тока позволяет оценить жизнеспособность этих тканей, что важно знать, например, при пересадке (трансплантации) тканей и органов. На рис.7 представлены частотная зависимость импеданса здоровой ткани (1) и мертвой (2), убитой кипячением в воде.
В мертвой ткани мембраны клеток разрушены и ткань обладает лишь активным сопротивлением, в то время как импеданс живой ткани складывается из активного и емкостного сопротивлений. Различие в частотных зависимостях импеданса получается и у здоровой, и у больной ткани.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ Упражнение 1. Определение индуктивности катушки
1. Проверить электрическую цепь (рис.8), состоящую из последовательно соединенных катушки индуктивности L, батареи конденсаторов C, амперметра A и реостата R.
2. Подключить вольтметр для измерения напряжения на катушке. 3. Поставить движок реостата в среднее положение. 4. Включить цепь и, изменяя сопротивление реостата, получить пять различных значений тока (в пределах от 0,1 до 0,3 A) и напряжения.
5. Вычислить индуктивное сопротивление катушки по формуле XL = где R - активное сопротивление катушки (указано на катушке). 6. Найти среднее значение XL и рассчитать индуктивность катушки:
7. Результаты измерений и вычислений занести в таблицу.
Сумма Среднее Упражнение 2. Определение емкости конденсатора 1. Переключить вольтметр для измерения напряжения на конденсаторе C. 2. Поставить движок реостата в среднее положение. 3. Включить цепь и, изменяя сопротивление реостата, получить пять различных значений силы тока и напряжения. 4. Вычислить емкостное сопротивление по формуле 5. Найти среднее значение
6. Результаты измерений и вычислений записать в таблицу.
Cумма Среднее Упражнение 3. Проверка закона Ома для полной цепи переменного тока
1. Переключить вольтметр для измерения напряжения на участке АВ, состоящем из последовательно включенных активного, индуктивного и емкостного сопротивлений. 2. Включить цепь и измерить одно значение напряжения и силы тока (в пределах 0,1 - 0,3 A) на этом участке. 3. Вычислить полное сопротивление участка АВ: 4. Рассчитать полное сопротивление участка АВ через средние значения индуктивного, емкостного и активного сопротивлений по формуле
и сравнить с результатом, полученным в пункте 3. 5. Результаты измерений и вычислений занести в протокол. Контрольные вопросы. 1. Переменный ток. 2. Уравнение и график гармонического тока. 3. Мгновенное, амплитудное и эффективное значение силы переменного тока и ЭДС. 4. Цепь переменного тока с активным сопротивлением R. 5. Цепь переменного тока с емкостным сопротивлением XC. 6. Цепь переменного тока с индуктивным сопротивлением XL. 7. Вывод закона Ома для полной цепи переменного тока. Импеданс цепи. 8. Понятие о сдвиге фаз в цепи переменного тока с XL, XC и в цепи с полным сопротивлением. В каких случаях сдвиг фаз равен нулю? 9. Понятие о резонансе напряжений. 10. Импеданс тканей организма. Эквивалентные схемы тканей.
11. Понятие о реографии, ее виды. Частотная зависимость импеданса тканей, ее использование в медицине.
Лабораторная работа №7
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 924; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.145.41 (0.012 с.) |

 .
. sinw t и di =
sinw t и di = 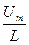 sinw tdt.
sinw tdt.  cosw t =
cosw t =  ), где
), где  - амплитуда тока.
- амплитуда тока. ,
, можно рассматривать как индуктивное сопротивление.
можно рассматривать как индуктивное сопротивление.
 .
.
 =
=  =
=
 .
.
 .
.


 ,
, , где w=2pn=2×50p =314 Гц.
, где w=2pn=2×50p =314 Гц. _________
_________ _________
_________ .
.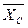 и рассчитать емкость конденсатора:
и рассчитать емкость конденсатора: .
.
 __________
__________ .
.



