
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение средней скорости перемещения органических удобренийСодержание книги
Поиск на нашем сайте
Решение основной задачи динамики сводится к тому, чтобы из данных уравнений, зная силы, найти закон движения точки, т.е. X=f(t). Для этого необходимо проинтегрировать соответствующие дифференциальные уравнения. Вернемся к уравнениям (3.108)
В общем случае уравнение (3.108) с математической точки зрения будет представлять собой дифференциальное уравнение 2-го порядка, имеющего общий вид где Чтобы решить основную задачу динамики, надо, кроме действующих сил, знать ещё начальные условия, т.е. положение и скорость точки в начальный момент. По начальным условиям можно определить частное решение дифференциального уравнения, дающее закон движения точки, в виде: X = f (tO, XO, ZO) Для решения данного дифференциального уравнения воспользуемся методом Рунге-Кутта четвертого порядка в системе MathCAD. Коэффициенты Рунге-Кутта определены как функции пользователя. Данный метод реализуется следующими выражениями на каждом шаге вычислений: X”+2 f wab (t) X’+F (X, t) = O (t) (3.109)
J (X, Z, t):= O (t) – F (x, t) - 2 f wab (t) Z X’’ = J (X, Z, t) Z = X’ N: = 10 H: = 1[N I: = 0….N
В системе MathCAD в таком виде формулы задавать нельзя, поскольку переменные k1, k2, k3 и k4, определяемые через индексированные переменные Xi, Zi, ti, должны быть индексированными переменными, т.е. элементами массивов. Для этого необходимо определить k1, k2, k3 и k4 как функции пользователя с аргументами, Xi, Zi, ti. Векторная запись итерационных уравнений задана следующими выражениями.
XO: = 0 Xi+1: = ti + h[ zi + K[Xi ,ti , Z]] (3.110) ZO 0 Zi+1 Zi + S [Xi, ti, Zi ]
При решении дифференциального уравнения (3.3.17) методом Рунге-Кутта, исследовалось влияние каждой силы на процесс виброперемещения материала методом исключения каждого из них из системы дифференциальных уравнений. Установлено, что сила Кориолиса не оказывает существенного влияния, как на характер перемещения, так и на значение скорости движения материала. Зависимости в обоих случаях идентичны и не значительно отличаются по значению (рис.3.61). Поэтому в дальнейших расчетах при определении скорости перемещения материала силой Кориолиса можно пренебречь. Рассматривая вибровысевающее устройство, как узел машины для внесения твердых органических удобрений, можно заранее ограничиться пределами изменения некоторых параметров. Очевидно, что угол наклона вибровысевающего устройства должен быть меньше угла, определяемого коэффициентом трения материала о поверхность вибровысевающего устройства. Длина грузонесущего органа вибрационного типа выбираются из условий, обеспечивающих наименьшие инерционные усилия. Для характеристик кривошипных механизмов с динамической стороны в работах М.Н. Летошнева, Б.Г. Турбина, А.В. Николаенко, Е.С. Босого установлены соотношения длины грузонесущего органа к радиусу кривошипа
Дифференциальные уравнения при решении методом Рунге-Кутта имеют вид
F (x, t): = f eab (t) x – wab (t)2 (L-X) q (t): = f [w2 r sin [a (t) k (t): = w2 r cos [a (t) y (t): = g [ sin [ 24 O (t): = q (t) +k (t) +y (t) z = X’
Решение заключается в нахождении ряда значений Xi, Zi, ti искомой зависимости при i, изменяющемся от 0 до N при шаге изменения x, равном h.
Рисунок 3.56- Исследование влияния силы Кориолиса на процесс виброперемещения.
Полученные зависимости (рис.3.56-3.57) характеризует изменение скорости перемещения твердых органических удобрений z, по времени t, и по длине грузонесущего органа Х L.
Рисунок 3.57 - Решение дифференциального уравнения методом Рунге-Кутта
Анализ полученных зависимостей позволяет выявить влияние амплитуды и частоты колебаний на скорость перемещения материала и определить характер перемещения. Кроме того, исследование данных зависимостей позволяет сделать некоторые ограничения в дальнейших исследованиях. При увеличении амплитуды колебаний вибровысевающего устройства до 6-8 см (рис.3.58) перемещение материала приобретает пульсирующий характер. Наиболее рациональным является амплитуда колебаний А=4 см, при котором характер перемещения материала является плавно нарастающим. Расчет средней скорости перемещения материала позволяет более четко представить физическую сущность процесса виброперемещения.
при α = 15о, L = 1 м, f = 0,5 Рисунок 3.58 - Зависимость скорости горизонтального перемещения от амплитуды и частоты колебаний грузонесущего органа. Зависимости скорости виброперемещения при различной частоте и амплитуде колебаний, при различной длине вибровысевающего устройства представлены графически (рис.3.58-3.59).
при L = 1 м, f = 0,5, А = 4 см Рисунок 3.59 - Зависимость скорости горизонтального перемещения от угла наклона грузонесущего органа. Установлено, что скорость перемещения ТОУ увеличивается с повышением амплитуды и частоты колебаний. При этом увеличивается как скорость, так и ускорение грузонесущего органа.
при α = 15о, f = 0,5, А = 4 см Рисунок 3.60 - Зависимость скорости горизонтального перемещения от длины грузонесущего органа
при α = 15о, f = 0,5, А = 4 см, ω = 30c-1
Рисунок 3.61 - Зависимость скорости горизонтального перемещения от коэффициента трения
Одному и тому же значению ускорения грузонесущего органа соответствует несколько скоростей перемещения груза, которые уменьшается по мере увеличения частоты колебаний грузонесущего органа. Поэтому в вибрационном устройстве с заданным ускорением грузонесущего органа А Зависимости влияния физико-механических свойств материала на скорость виброперемещения показывают, что с увеличением величины коэффициента трения скорость виброперемещения уменьшается. Увеличение угла наклона грузонесущего органа вызывает увеличение скорости виброперемещения. Очевидно, что угол наклона вибровысевающего устройства должен быть меньше угла, определяемого коэффициентом трения материала о поверхность днища вибровысевающего устройства f. В противном случае материал, находящийся внутри бункера, всегда будет иметь потенциальную возможность к самоистечению из бункера. С увеличением длины вибровысевающего устройства скорость перемещения частицы уменьшается.
В результате построения графиков получена прямолинейная зависимость между исследуемыми величинами. Поэтому заранее можно сказать, что аналитическая зависимость между исследуемыми величинами может быть представлена уравнением прямой в виде y = a + b x Положение прямой на графике и её наклон определяются коэффициентами a и b, которые и следует определить при выводе частной эмпирической формулы. Сделать это можно, используя опытные данные, соответствующие двум точкам, расположенным на полученной прямой.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 354; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.205.123 (0.011 с.) |



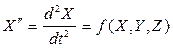






 .
. ] + eab (t) L]
] + eab (t) L]




 R=4 см
R=4 см
 0
0
 R=3 см
R=3 см

 R=6 см
R=6 см
















 рекомендуется как для снижения динамических нагрузок в системе, так и для повышения скорости перемещения применять меньшие значения частоты и большие значения амплитуд колебаний. Это подтверждено исследованиями других авторов [5,14,16].
рекомендуется как для снижения динамических нагрузок в системе, так и для повышения скорости перемещения применять меньшие значения частоты и большие значения амплитуд колебаний. Это подтверждено исследованиями других авторов [5,14,16].


