Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение усилий на рабочий орган от сопротивления почвыСодержание книги
Поиск на нашем сайте
Одной из сложных задач при движении рабочего органа в почве является достоверное описание напряженно-деформированного состояния почвы. Моделирование процесса обработки почвы позволяет определить рациональные параметры и режимы работы проектируемых почвообрабатывающих машин, установить функциональные зависимости агробиологической (АС) и механико-технологической систем (МТС), которые обеспечивали бы выполнение агротехническим требованиям АТТ. Почва, в отличие от сплошных деформируемых сред, является многофазной с неоднородной структурой и при деформации происходит ее разрушение; при взаимодействии почвы с рабочими органами непрерывно меняется ее плотность. Решение задачи по описанию НДС почвы возможно при определенных ограничениях: технологических, конструктивных и т.д., а полученные параметры имеют решение в условиях действующих ограничений. Имеются примеры построения достаточно точных математических моделей грунтов - сред, достаточно близких по своим свойствам к почве. Известны работы по моделированию воздействия рабочих органов плуга на почву [167,168]. Среди различных численных методов механики сплошных сред наиболее популярным - является метод конечных элементов (МКЭ). Геометрические параметры рабочего органа определяются при построении в системе автоматизированного проектирования (САПР). Спроек-тированный рабочий орган импортируется в среду FlowVision, где заранее определена область расчета, в котором заданы уравнения математической модели, и граница, с определенными на ней граничными условиями. На основе этой модели рассматривается процесс взаимодействия рабочего органа со средой и получена объемная картина деформирования среды (рис.3.6), распределение давлений перед рабочим органом и непосредственно на нем, значения сил и моментов, действующих на рабочий орган.
Рисунок 3.6 -Изолинии давления перед корпусом плуга в среде FlowVision [167]
Разработанная модель в среде FlowVision позволяет установить характеристики деформации, перемещения и перемешивания почвы, силовую нагруженность рабочего органа. Полученные результаты исследований путем моделирования позволяют получить представление по описанию НДС почвы при определенных ограничениях. Однако достоверность теоретических исследований достаточно тяжело подтвердить в лабораторных исследованиях.
Известны исследования В.АЖилкина, М.С.Баган для решения плоских задач механики сплошной среды. В работе [19] выбрана имеющая аналитическое решение задача о давлении плоского жесткого штампа на упругую полуплоскость из крупнозернистого сухого песка. Нагружение штампа осуществлялось в нагрузочной рамке. Для определения величины перемещений применен метод голографической интерферометрии (рис.3.7). Изолинии уровня полей перемещений и и v песчаного основания, найденные при решении упругой задачи методом моделирования, приведены на рис.3.8. Математическая модель песка сформулирована в виде системы уравнений, описывающих объёмное сжатие и упругопластический сдвиг [19]:
где K - модуль объемного сжатия; Sij,
Рис. 3.8 - Изолинии вертикальных u (а) и горизонтальных v (б) перемещений точек песчаной среды, в мкм (усложненная модель среды)
Сопоставление рис.3.7 и рис.3.8 позволяет сделать вывод об удовлетворительном совпадении экспериментальных и численных результатов и наглядно демонстрирует различие в моделях упругой среды и среды с нелинейными законами объемного деформирования среды с переменными модулями объемного сжатия. Приведенный пример иллюстрирует возможности решения контактной задачи о взаимодействии почвы и рабочих органов. Теория упругости может дать только грубое приближение НДС для предельного состояния почвы, а определение размеров комков почвы, образовавшихся в процессе взаимодействия рабочего органа с почвой только средствами теории упругости получить невозможно. При обосновании рабочего органа фрезерного грядообразователя ограничимся решением упругих задач взаимодействия рабочего органа почвообрабатывающей машины в виде стержня круглого поперечного сечения с упругой полуплоскостью (почвой). Для рассматриваемого случая контактного взаимодействия стержня и полуплоскости фактически принимается гипотеза о затухании напряженно-деформированного состояния (НДС) на незначительном удалении от зоны контакта и тем самым постулируется возможность рассмотрения локального НДС в зоне контакта независимо от макроскопического НДС объекта в целом.
Принято допущение, что НДС затухает на расстоянии в шесть раз превышающем зону контакта (из результатов последующего решения поставленной задачи следует, что эта гипотеза выполняется частично)[90,91]. Упрощение реальной задачи связано с существенными трудностями ее решения в целом. Скорость торца стержня не превышает
В связи с этим задачу деформирования почвы стержнем можно рассматривать как квазистатическую. В данной работе мы рассмотрим только статическую задачу. Требуется исследовать напряженно-деформированное состояние упругой полуплоскости толщиной В качестве глобальной системы координат принята декартовая с началом в неподвижном центре. В соответствии с принципом Сен-Венана примем «бесконечность» на расстоянии
Рисунок 3.9 - Расчетная схема напряженно-деформированного состояния упругой полуплоскости Для материала полуплоскости «Soil» приняты следующие физические характеристики: Загружаем создаваемую модель взаимодействия стержня и полуплоскости заданной нагрузкой – крутящим моментом
Рисунок 3.10 – Схема деформированной полуплоскости и контактирующего с ней стержня
Из рис.3.10 следует, что деформации стержня не противоречат физическому смыслу задачи, а так как выбрана точка
В соответствии с рис.3.10 максимальные нелинейные напряжения не превышают
Рисунок 3.11 – Схема эквивалентных напряжений Мизеса
Рисунок 3.12 - Картины полос для полей главных напряжений
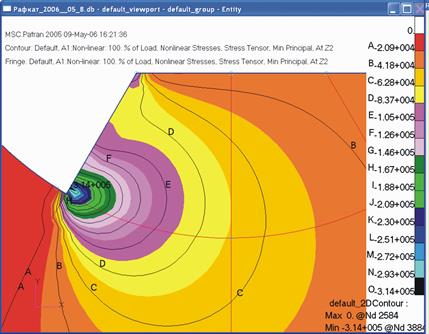
Рисунок 3.14 - Напряженно-деформированное состояние полуплоскости при угле вхождения рабочего органа на 90о
Рисунок 3.15 - Напряженно-деформированное состояние полуплоскости при угле вхождения рабочего органа на 120о Исследуя деформированное состояние полуплоскости получим картину эквивалентных напряжений Мизеса, представленную в виде цветных полос рис.3.14. В 1904 г. польский ученый М. Т. Губер предложил считать удельную потенциальную энергию формоизменения в качестве фактора, определяющего наступление в материале предельного состояния. Гипотеза формулируется так: предельное состояние материала наступает при достижении удельной потенциальной энергией формоизменения в окрестности рассматриваемой точки тела предельной (опасной) величины.
Рисунок 3.13 - Картины полос для полей главных напряжений
Критерий предельного состояния материала в окрестности рассматриваемой точки тела выглядит на основе гипотезы Губера так:
где В 1913 г. Мизес, желая упростить предельную поверхность третьей теории прочности, так же пришел к соотношению (3.17). С тех пор критерий (3.37) называют условием пластичности Мизеса-Генки, а левую часть равенства (3.37) эквивалентными напряжениями Мизеса. Из рис.3.14 и 3.15 следует, что за рабочим органом дневная поверхность почвы может быть покрыта трещинами, ориентированными вдоль оси вращения рабочего органа, а у свободного торца рабочего органа может образоваться уплотненное ядро, физико-механические характеристики которого будут отличаться от принятых в расчете. Для уточнения результатов расчета его целесообразно повторить, приняв во внимание уплотненное ядро почвы. Наиболее нагруженной оказалась точка в зоне пересечения цилиндрической поверхности и плоскости с нормалью составляющей угол
Анализ графического материала позволяет определить величину сопротивления почвенной среды создаваемую рабочим органом и иллюстрирует возможности решения задачи о величине тягового сопротивления почвообрабатывающего орудия. Решение данной задачи возможно при определении предельного значения крутящего момента Предельное значение крутящего момента на валу фрезерного барабана определяется по выражению
где Rпр - равнодействующая предельного сопротивления на рабочем органе фрезерного барабана; l - расстояние от центра фрезерного барабана до места приложения равнодействующей предельного сопротивления; L – длина рабочего органа фрезерного барабана,м; G - сила тяжести вырезаемого блока, кг; z – число рабочих органов в одной плоскости. Рассматривая схему (рисунок 3.16) необходимо отметить, что нормальные составляющие напряжения почвы - постоянная величина, поэтому в дальнейших расчетах она не рассматривается.
Рисунок 3.16 – Схема для определения сил сопротивления почвенной среды
Рассматривая схему (рисунок 3.16) необходимо отметить, что нормальные составляющие напряжения почвы - постоянная величина, поэтому в дальнейших расчетах она не рассматривается. С учетом допущения о направленности касательных составляющих -t к центру этими силами также можно пренебречь. Равнодействующая предельного сопротивления на рабочем органе фрезерного барабана
где Значение равнодействующей предельного сопротивления на рабочем органе позволяет определить величину сопротивления почвенной среды создаваемую рабочим органом и определить величину тягового сопротивления тягово-приводного почвообрабатывающего орудия и энергетические показатели агрегата. Мощность на резание и отбрасывание почвы фрезерным барабаном определим из работы, расходуемой на фрезерование почвы при одном обороте барабана, А = 2 p Мкр, где Мкр - приводной момент на валу барабана. Разделив эту работу на обрабатываемый объем почвы- V за один оборот барабана, получим удельную работу.
Преобразовав (3.21) получим
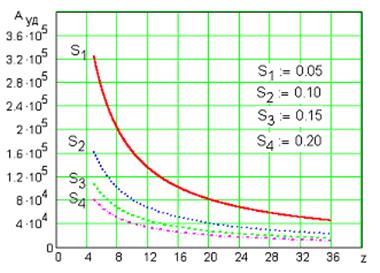
Рисунок 3. 17 Зависимость удельной работы от подачи и глубины обработки
Рисунок 3. 18 Зависимость удельной работы от подачи и количества ножей
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 498; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.45.159 (0.013 с.) |



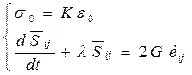 (3.15)
(3.15) - компоненты девиаторов напряжения и скоростей деформаций; тильда означает производную по Яуманну.
- компоненты девиаторов напряжения и скоростей деформаций; тильда означает производную по Яуманну.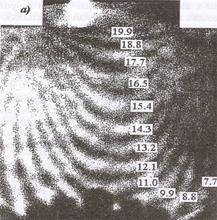

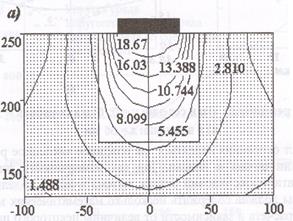 Рис. 3.7 - Картина интерференционных полос, наблюдаемых в плоскостях XZ (а) и YZ (б).
Рис. 3.7 - Картина интерференционных полос, наблюдаемых в плоскостях XZ (а) и YZ (б).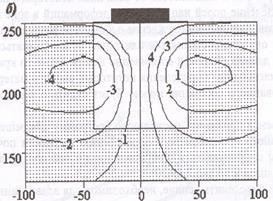
 м/с. Если рассматривать почву как изотропную среду с модулем упругости
м/с. Если рассматривать почву как изотропную среду с модулем упругости 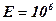 Н/м2, коэффициентом Пуассона
Н/м2, коэффициентом Пуассона  [1]и плотностью среды
[1]и плотностью среды  г/см3 [2], то скорость распространения продольных волн в среде приближенно в двадцать два раза превышает скорость деформирования почвы.
г/см3 [2], то скорость распространения продольных волн в среде приближенно в двадцать два раза превышает скорость деформирования почвы. м/с. (3.16)
м/с. (3.16) м взаимодействующей со стальным стержнем круглого поперечного сечения, поворачивающимся относительно неподвижного центра, совпадающим с одним из торцов стержня. Неподвижный центр расположен на расстоянии
м взаимодействующей со стальным стержнем круглого поперечного сечения, поворачивающимся относительно неподвижного центра, совпадающим с одним из торцов стержня. Неподвижный центр расположен на расстоянии  м от дневной поверхности полуплоскости. Предполагается, что стержень внедряется в полуплоскость и ось стержня составляет угол кратный
м от дневной поверхности полуплоскости. Предполагается, что стержень внедряется в полуплоскость и ось стержня составляет угол кратный  с линией отвеса. Длины зон контакта стержня и полуплоскости
с линией отвеса. Длины зон контакта стержня и полуплоскости 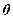 м,
м,  м и
м и 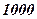 Н.м. Случай, когда стержень соприкасается с полуплоскостью, соответствует решению Фламана и потому в данной работе не рассматривается.
Н.м. Случай, когда стержень соприкасается с полуплоскостью, соответствует решению Фламана и потому в данной работе не рассматривается.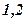 м, т. е. будем считать, что на этом расстоянии перемещения точек полуплоскости равны нулю (рис.3.9).
м, т. е. будем считать, что на этом расстоянии перемещения точек полуплоскости равны нулю (рис.3.9).
 Н/м2 и
Н/м2 и  ; для материала стального стержня «st»:
; для материала стального стержня «st»:  Н/м2 и
Н/м2 и  . Толщину полуплоскости примем равной
. Толщину полуплоскости примем равной  м, и для круглого поперечного сечения стержня - радиус круга
м, и для круглого поперечного сечения стержня - радиус круга  м.
м.
 (рис.3.10 в), лежащая на нейтральной оси, то напряжения в этом волокне стержня равны нулю (в системе Patran-Nastran напряжения по умолчанию выводятся только в четырех точках, фиксированных для каждого типа поперечного сечения). Если выбрать точку (рис.3.10, в), то появится информация о напряжениях в наиболее нагруженном волокне стержня (рис.3.10,б).
(рис.3.10 в), лежащая на нейтральной оси, то напряжения в этом волокне стержня равны нулю (в системе Patran-Nastran напряжения по умолчанию выводятся только в четырех точках, фиксированных для каждого типа поперечного сечения). Если выбрать точку (рис.3.10, в), то появится информация о напряжениях в наиболее нагруженном волокне стержня (рис.3.10,б). МПа. Полные напряжения не превышают
МПа. Полные напряжения не превышают 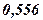 МПа. Аналогично получаем картины полос для полей главных напряжений
МПа. Аналогично получаем картины полос для полей главных напряжений  - растягивающих (рис.3.11) и
- растягивающих (рис.3.11) и 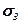 - сжимающих (рис.3.12). Нормальные напряжения в опасной точке стержня не превышают допускаемых (для малоуглеродистой стали
- сжимающих (рис.3.12). Нормальные напряжения в опасной точке стержня не превышают допускаемых (для малоуглеродистой стали 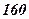 МПа).
МПа).



 (3.17)
(3.17)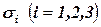 - главные напряжения;
- главные напряжения;  - напряжения текучести.
- напряжения текучести. с осью
с осью  -
- 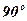 и
и  с линией отвеса, получим напряженно-деформированное состояние полуплоскости, приведенное на рис.3.14 и 3.15.
с линией отвеса, получим напряженно-деформированное состояние полуплоскости, приведенное на рис.3.14 и 3.15. необходимого для обеспечения прохождения рабочего органа в почве.
необходимого для обеспечения прохождения рабочего органа в почве.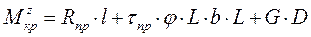 (3.18)
(3.18)
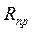 определяется по выражению
определяется по выражению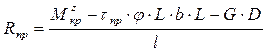 (3.19)
(3.19)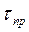 - справочное значение касательного напряжения;
- справочное значение касательного напряжения;  - угол наклона рабочего органа,град; L - длина рабочего органа,м;
- угол наклона рабочего органа,град; L - длина рабочего органа,м;  - площадь подвергаемая обработке,м2;
- площадь подвергаемая обработке,м2;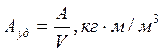 (3.20)
(3.20) . (3.21)
. (3.21)