
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение уравнения движения точки пальца бесприводного рабочего органа с наклонной осью вращенияСодержание книги
Поиск на нашем сайте
Внешний вид бесприводного ротационного рабочего органа c наклонной осью вращения приведен на рис.3.29. Рабочий орган приводится в движение за счёт взаимодействия пальцев, выполняющих функцию привода рабочего органа, с почвой и участвует в двух движениях: поступательном и вращательном.
Рисунок 3.29 –Бесприводной ротационный рабочий орган Если бы рабочий орган не был бы наклонен в поверхности поля, то траектория точек обода колеса имела бы вид, приведенный на рис.3.29 (рис.3.30,б). Колесо вращается относительно оси
Рисунок 3.30 - Траектория точек бесприводного ротационного рабочего органа Любая точка на поверхности пальца бесприводного ротационного рабочего органа с предлагаемой конструктивной схемой (рис.3.30) совершает сложное движение, описываемое параметрическим уравнением (3.48). Уравнения движения пальца в системе координат
Следовательно, радиус вектор точки
Составим таблицу 3.3 направляющих косинусов единичных векторов Таблица 3.3.- Направляющие косинусов единичных векторов
Проектируя обе части равенства (3.49) на оси
Траекторию крайней точки VM: =2.5 R: = 0.25 φ: = 15 deg b: = deg
Траектория точки
Рисунок 3.31 - Траектория движения точки Зависимость для определения абсолютной скорости точки, совершающей сложное движение в пространстве, в общем виде имеет вид:
где Для определения абсолютной скорости точки, совпадающей с концом пальца (м/с) секции рабочего органа найдём значения её составляющих:
Подставив выражения (3.56) в (3.55) получим:
Характер изменения абсолютной скорости движения пальца в зависимости от угла поворота рабочего органа
Рисунок 3.32 – Зависимость абсолютной скорости пальца от угла поворота секции рабочего органа (при R=0,7 м и V=2 м/с): 1 – при α = 0,175 рад (10 град); 2 – α = 0,35 рад (20 град); 3 – α = 0,525 рад (30 град)
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 481; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.163.23 (0.009 с.) |


 , плоскость колеса совпадает с плоскостью
, плоскость колеса совпадает с плоскостью 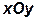 . Центр колеса движется со скоростью
. Центр колеса движется со скоростью  , направленной горизонтально в направлении движения трактора и совпадающей с осью
, направленной горизонтально в направлении движения трактора и совпадающей с осью  неподвижной системы координат. В базисе
неподвижной системы координат. В базисе  вектор
вектор  ;
;  ,
, 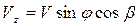 . Переход от неподвижной системы координат
. Переход от неподвижной системы координат  к системе координат
к системе координат  осуществляется двумя поворотами относительно осей
осуществляется двумя поворотами относительно осей 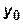 на угол
на угол  и оси
и оси  на угол
на угол  (рис.3.30, а).
(рис.3.30, а).
 (3.48)
(3.48) будет
будет . (3.49)
. (3.49) ,
,  ,
,  в базисе
в базисе 


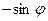






 и учитывая таблицу косинусов, найдём проекции радиус вектора
и учитывая таблицу косинусов, найдём проекции радиус вектора  на эти оси
на эти оси (3.50)
(3.50)

 (3.51)
(3.51)
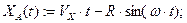 (3.52)
(3.52)
 (3.53)
(3.53) (3.54)
(3.54)

 (3.54)
(3.54)
 (3.55)
(3.55)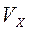 ,
, 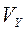 и
и 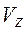 - составляющие абсолютной скорости пальца, м/с
- составляющие абсолютной скорости пальца, м/с (3.56)
(3.56) (3.57)
(3.57) показан на рисунке 3.32. Изменение угла наклона оси вращения секции оказывает незначительное влияние на величину абсолютной скорости пальца.
показан на рисунке 3.32. Изменение угла наклона оси вращения секции оказывает незначительное влияние на величину абсолютной скорости пальца.



