
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 1. Расчет на прочность балки на двух опорах по методуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Утверждено на заседании кафедры сопротивления материалов 23 ноября 2007 г.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по выполнению расчетно-графической работы по сопротивлению материалов «РАСЧЕТ БАЛОК НА ПРОЧНОСТЬ»
Ростов-на-Дону
УДК 620.178.32 (076.5)
Методические указания по выполнению расчетно-графической работы по сопротивлению материалов «Расчет балок на прочность». – Ростов н/Д: Рост. гос. строит. ун-т, 2008. – 20 с.
Содержат основные теоретические положения, примеры и порядок выполнения студентами расчетно-графической работы по сопротивлению материалов «Расчет балок на прочность». Рассчитаны на студентов очного обучения.
Составители: канд. техн. наук, доц. В.П. Бондаренко канд. физ.-мат. наук, доц. Г.П. Стрельников
Редактор Т.М. Климчук Темплан 2008г., поз. 136 Подписано в печать 16.04.08. Формат 60х84/16. Бумага писчая. Ризограф. Уч.-изд.л. 1,2. Тираж 200 экз. Заказ
Редакционно-издательский центр Ростовского государственного строительного университета. 344022, Ростов-на-Дону, Социалистическая, 162.
строительный университет, 2008
В расчетно-графической работе «Расчет балок на прочность» студенту предлагается выполнить расчет двух типов балок различной формы поперечного сечения. В настоящем руководстве рассматриваются примеры решения задач в объеме, требуемом методическими указаниями.
Задача 1. Расчет на прочность балки на двух опорах по методу Допускаемых напряжений
Исходные данные: с = 2 м; b = 4 м; а = 1 м; q = 10 кН/м; m =19 кНм; F =12 кН; b = h/b = 2, 5 Рис.1
Для заданной расчетной схемы балки на двух опорах (рис.1) требуется:
1.Определить опорные реакции.
2.Построить эпюры поперечных сил (Q) и изгибающих моментов(M).
нормальных напряжений подобрать размеры прямоугольного сечения (рис.2) деревянной балки при заданных соотношениях b = h / b. Принять допускаемое нормальное напряжение [ s ]=12МПа.
4.Проверить прочность подобранного сечения по Рис.2 касательным напряжениям, приняв [ t ]=2МПа.
касательных напряжений по высоте балки.
6.Для этой же балки подобрать круглое поперечное сечение диаметром d (рис.3), приняв допускаемое нормальное напряжение [ s ]=12МПа.
Рис.3
Решение Определение опорных реакций Для балки, изображенной на рис.4, составляем три уравнения статики:
S F x = 0: - HA= 0; HA= 0. S M A = 0: F ·2 - q ·4·2 – m + RB ·5=0;
-75 + R B ·5=0; S M B = 0: - F ·7 - RA ·5 + q ·4·3 - m =0;
- 185 - RA ·5=0;
Ком пунктиром показаны положения растянутых волокон. Построение эпюр нормальных и касательных напряжений В опасных сечениях В опасном сечении балки Mmax =24 кНм=2400 кНсм, растянуты верхние волокна (см. эпюру изгибающих моментов), поэтому нормальные напряжения в точках, лежащих на линии 1 – 1 – положительные, а в точках, лежащих на линии 3 – 3 – отрицательные (рис.6).
Напряжение в точках линии 1 – 1
Напряжение в точках линии 3 – 3
Используя полученные данные, строим эпюру нормальных напряжений по высоте балки, которая графически изображается наклонной прямой линией (рис.6). Опасными точками поперечного сечения называются точки, напряжения в которых достигают наибольших по величине значений.
В нашей задаче точки, лежащие на линиях 1 – 1 и 3 – 3, являются опасными по нормальным напряжениям. Обратите внимание, что они наиболее удалены от нейтральной линии (ось y).
Рис.6
Переходим к построению эпюры касательных напряжений. Как было показано выше, максимальные касательные напряжения возникают в точках сечения, лежащих на линии 2 – 2
В точках сечения, лежащих на линиях 1 – 1 и 3 – 3, касательные напряжения равны 0
Используя полученные данные и учитывая, что касательные напряжения по высоте поперечного сечения изменяются по параболическому закону, строим эпюру касательных напряжений, как это показано на рис.6 Точки, лежащие на линии 2 – 2, являются опасными точками по касательным напряжениям.
6. Подбор круглого сечения деревянной балки по методу допускаемых напряжений (рис.7)
Момент сопротивления круга диаметром d определяется по формуле
Приравнивая Из полученного соотношения определяем размер d Рис.7 d Окончательно диаметр круглого сечения балки, с учетом технологических требований, принимаем d = 27, 5 cм. Проверим выполнение условия прочности. С этой целью определяем фактический момент сопротивления
Находим максимальное нормальное напряжение
Условие прочности выполняется.
Решение
Расчет балки с промежуточным шарниром проведем методом составления поэтажной схемы (рис.9)
Рис.9
Для этого балка разрезается по промежуточному шарниру (шарнирам) и выделяются основная и подвесные балки. Основной является та балка, которая может самостоятельно нести внешнюю нагрузку после разрезания по промежуточному шарниру (балка AB на рис.9). Подвесная же балка не может работать самостоятельно вследствие недостаточности связей, закрепляющих ее от смещения как абсолютно твердого тела (балка BC на рис. 9). Расчет балок производят отдельно, начиная с подвесных балок. При последующем расчете основной балки, кроме заданных внешних нагрузок, к ней должны быть приложены реакции взаимодействия с подвесными балками.
1.Определение опорных реакций и построение эпюр Q и M подвесной балки BC (рис.10) a) Определение опорных реакций S F x = 0: - HB= 0; HB= 0.
S M B = 0: - q ·3·1,5 + RС ·2+ m =0;
-72 + RС ·2=0;
S MC= 0: - RB ·2 + q ·3·0,5 + m =0; - RB ·2 + 20·1,5 +18 =0;
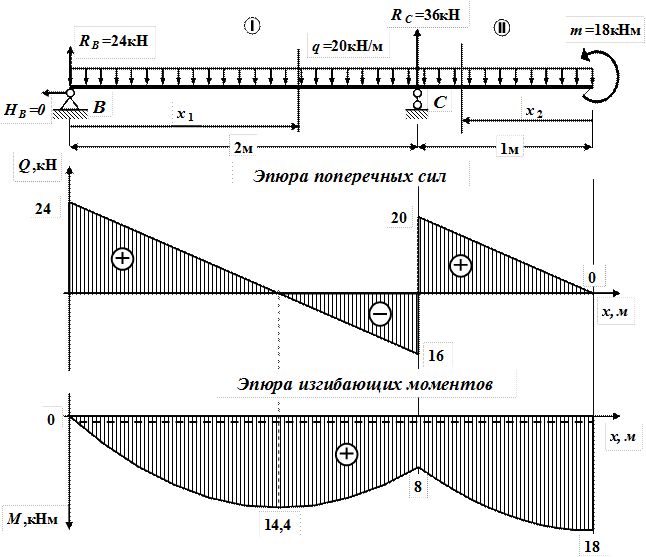 - RB ·2 +48 =0; - RB ·2 +48 =0;
Рис.10
Напряжений
В опасном сечении по нормальным напряжениям (сечение A на рис.12)
Из условия прочности (1) определяем требуемую величину момента сопротивления
Рис.12
По сортаменту прокатной стали ближайшим к Итак, для двутавра №33 фактический момент сопротивления
Рис.13 Проверяем выполнение условия прочности:
Условие прочности выполняется. Балка недогружена. Выбираем двутавр №33.
Замечание. Метод расчета по допускаемым напряжениям допускает пере- грузку балок в пределах 5 %.Т.е. величина перегрузки
Проведем теперь подбор сечения, состоящего из двух швеллеров (рис.14) (для нечетных схем). Момент сопротивления относительно оси y
Здесь с индексом “ шв” обозначается момент инерции и момент сопротивления одного швеллера, а без индекса - момент инерции и момент сопротивления двух швеллеров. Рис.14 Приравнивая противления одного швеллера должен удовлетворять условию
По сортаменту прокатной стали (прил.2) выбираем швеллер № 27, т.к. его момент сопротивления
Для выбранного сечения проверяем выполнение условия прочности:
Условие прочности выполняется. Выбираем сечение из швеллеров № 27. Напряжениям Касательные напряжения (t) в произвольной точке поперечного сечения определяются по формуле Д.И. Журавского
где Q - абсолютная величина поперечной силы (определяется по эпюре поперечных сил);
части фигуры; b (z) - толщина поперечного сечения на расстоянии z от оси y;
Максимальные касательные напряжения определяются в опасном сечении (Q = Q max) в точках поперечного сечения, лежащих на оси y, поэтому b (z)= d для двутавра и b (z)=2 d для двух швеллеров. Отсеченная часть - верхняя половина поперечного сечения, поэтому Условие прочности по касательным напряжениям записывается в виде
где [ t ] - допускаемое касательное напряжение. Для стальных элементов [ t ]= 0, 6[ s ]. В нашем примере опасным сечением по касательным напряжениям является сечение А (рис.12) Q max = 44 кН Из сортамента прокатной стали для двутавра №33 определяем следующие значения: h =33 см; b =14 см; d =0,7 см; t =1,12 см; J y=9840 см4; Проверяем выполнения условия прочности (4)
Условие прочности по касательным напряжениям выполняется. Определяем максимальное касательное напряжение для сечения из двух швеллеров №27. Из сортамента прокатной стали для швеллера №27 определяем следующие значения:
h =27 см; b =9,5 см; d =0,6 см; t =1,05 см; J y=4160 см4;
Условие прочности по касательным напряжениям для двух швеллеров №27 выполняется. Утверждено на заседании кафедры сопротивления материалов 23 ноября 2007 г.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по выполнению расчетно-графической работы по сопротивлению материалов «РАСЧЕТ БАЛОК НА ПРОЧНОСТЬ»
Ростов-на-Дону
УДК 620.178.32 (076.5)
Методические указания по выполнению расчетно-графической работы по сопротивлению материалов «Расчет балок на прочность». – Ростов н/Д: Рост. гос. строит. ун-т, 2008. – 20 с.
Содержат основные теоретические положения, примеры и порядок выполнения студентами расчетно-графической работы по сопротивлению материалов «Расчет балок на прочность». Рассчитаны на студентов очного обучения.
Составители: канд. техн. наук, доц. В.П. Бондаренко канд. физ.-мат. наук, доц. Г.П. Стрельников
Редактор Т.М. Климчук Темплан 2008г., поз. 136 Подписано в печать 16.04.08. Формат 60х84/16. Бумага писчая. Ризограф. Уч.-изд.л. 1,2. Тираж 200 экз. Заказ
Редакционно-издательский центр Ростовского государственного строительного университета. 344022, Ростов-на-Дону, Социалистическая, 162.
строительный университет, 2008
В расчетно-графической работе «Расчет балок на прочность» студенту предлагается выполнить расчет двух типов балок различной формы поперечного сечения. В настоящем руководстве рассматриваются примеры решения задач в объеме, требуемом методическими указаниями.
Задача 1. Расчет на прочность балки на двух опорах по методу Допускаемых напряжений
Исходные данные: с = 2 м; b = 4 м; а = 1 м; q = 10 кН/м; m =19 кНм; F =12 кН; b = h/b = 2, 5 Рис.1
Для заданной расчетной схемы балки на двух опорах (рис.1) требуется:
1.Определить опорные реакции.
2.Построить эпюры поперечных сил (Q) и изгибающих моментов(M).
нормальных напряжений подобрать размеры прямоугольного сечения (рис.2) деревянной балки при заданных соотношениях b = h / b. Принять допускаемое нормальное напряжение [ s ]=12МПа.
4.Проверить прочность подобранного сечения по Рис.2 касательным напряжениям, приняв [ t ]=2МПа.
касательных напряжений по высоте балки.
6.Для этой же балки подобрать круглое поперечное сечение диаметром d (рис.3), приняв допускаемое нормальное напряжение [ s ]=12МПа.
Рис.3
Решение Определение опорных реакций Для балки, изображенной на рис.4, составляем три уравнения статики:
S F x = 0: - HA= 0; HA= 0. S M A = 0: F ·2 - q ·4·2 – m + RB ·5=0;
-75 + R B ·5=0; S M B = 0: - F ·7 - RA ·5 + q ·4·3 - m =0;
- 185 - RA ·5=0;
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 1951; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.73.167 (0.009 с.) |

 С Ростовский государственный
С Ростовский государственный
 3.Из условия прочности по методу допускаемых
3.Из условия прочности по методу допускаемых 5.Для опасных сечений построить эпюры нормальных и
5.Для опасных сечений построить эпюры нормальных и 15 кН.
15 кН.
 37 кН.
37 кН.
 11,6 МПа.
11,6 МПа. –11,6 МПа.
–11,6 МПа.
 .
.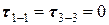 .
.
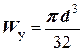 .
. , получаем
, получаем  .
.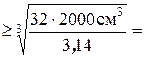 27,316 cм.
27,316 cм.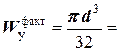
 204 0,69 см3=2040 см3.
204 0,69 см3=2040 см3.
 1,17 6
1,17 6 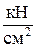 =11,8 МПа < 12 МПа.
=11,8 МПа < 12 МПа.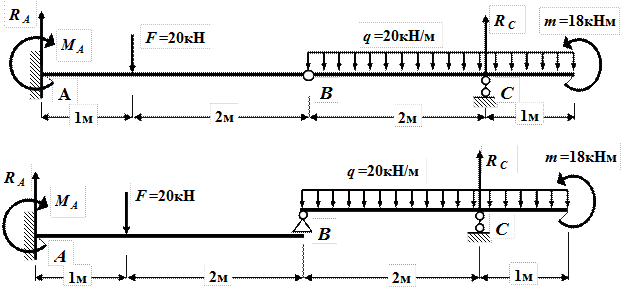
 36 кН.
36 кН.
 24 кН.
24 кН.
 92 кНм=9200 кНсм.
92 кНм=9200 кНсм.
 = 575 см3;
= 575 см3;
 Вначале проведем подбор двутаврового сечения (рис.13) (для четных схем).
Вначале проведем подбор двутаврового сечения (рис.13) (для четных схем). является значение момента сопротивления
является значение момента сопротивления  = 597 см3 , которое соответствует двутавру №33.
= 597 см3 , которое соответствует двутавру №33. 597см3.
597см3. 15,4 104
15,4 104  154 МПа < [ s ]=160 МПа.
154 МПа < [ s ]=160 МПа.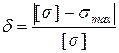
 5 %.
5 %.
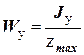 , но
, но 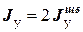 , поэтому
, поэтому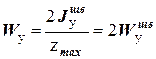 .
. и
и 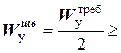
 см3.
см3.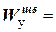 308 см3, тогда фактический момент сопротивления
308 см3, тогда фактический момент сопротивления =2·308 см3=616 см3.
=2·308 см3=616 см3. 14,9 4
14,9 4  , (3)
, (3) - абсолютное значение статического момента площади отсеченной
- абсолютное значение статического момента площади отсеченной - осевой момент инерции.
- осевой момент инерции.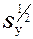 - для двутавра и
- для двутавра и  [ t ], (4)
[ t ], (4) 339 см4.
339 см4.
 2,16 55
2,16 55  = 21,7 МПа < 96 МПа.
= 21,7 МПа < 96 МПа.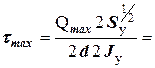
 = 1,56 89
= 1,56 89 


