
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Подбор прямоугольного сечения деревянной балки по методуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
допускаемых напряжений
Условие прочности при изгибе по нормальным напряжениям по методу допускаемых напряжений имеет вид: s max В этой формуле: s max - максимальное нормальное напряжение; Mmax - максимальное по абсолютной величине значение изгибающего момента (определяется по эпюре изгибающих моментов); [ s ] - допускаемое нормальное напряжение.
Сечение, в котором изгибающий момент принимает максимальное по абсолютной величине значение, называют опасным сечением балки по нормальным напряжениям.
Из условия прочности (1) определяется требуемая величина момента сопротивления по формуле:
Размеры сечения подбираются из условия:
В опасном сечении по нормальным напряжениям M max=24 кНм=2400кНсм, растянуты верхние волокна (см. эпюру изгибающих моментов). Из условия прочности определяем требуемую величину момента сопротивления
Используя заданное в условии соотношение b = h/b = 2,5 выражаем момент сопротивления через один из размеров, например b (h = 2,5 b),
Рис.5 Приравнивая Из полученного соотношения определяем размер b b Принимаем b =12,5 см. Тогда h = 2,5 b = 2,5·12,5 см= 31,2 5 см =31, 5 см.
Замечание. Размеры сечений деревянных элементов, согласно требованиям технологии, округляются до размера кратного 0,5см. Проверяем выполнение условия прочности. С этой целью определяем фактический момент сопротивления
Находим максимальное нормальное напряжение
Условие прочности выполняется.
Проверка прочности подобранного сечения балки по касательным напряжениям
Сечение, в котором поперечная сила принимает максимальное по абсолютной величине значение, называют опасным сечением балки по касательным напряжениям. Максимальные касательные напряжения возникают в опасном сечении балки в точках сечения, лежащих на нейтральном слое и для прямоугольного сечения вычисляется по формуле
где A = bh – площадь поперечного сечения. Условие прочности записывается в виде
Здесь Q - максимальное по абсолютной величине значение поперечной си- лы (определяется по эпюре поперечных сил); [ t ] - допускаемое касательное напряжение. При принятых размерах сечения b =12,5 см, h = 31, 5 см.
Условие прочности по касательным напряжениям выполняется.
Построение эпюр нормальных и касательных напряжений В опасных сечениях В опасном сечении балки Mmax =24 кНм=2400 кНсм, растянуты верхние волокна (см. эпюру изгибающих моментов), поэтому нормальные напряжения в точках, лежащих на линии 1 – 1 – положительные, а в точках, лежащих на линии 3 – 3 – отрицательные (рис.6).
Напряжение в точках линии 1 – 1
Напряжение в точках линии 3 – 3
Используя полученные данные, строим эпюру нормальных напряжений по высоте балки, которая графически изображается наклонной прямой линией (рис.6). Опасными точками поперечного сечения называются точки, напряжения в которых достигают наибольших по величине значений.
В нашей задаче точки, лежащие на линиях 1 – 1 и 3 – 3, являются опасными по нормальным напряжениям. Обратите внимание, что они наиболее удалены от нейтральной линии (ось y).
Рис.6
Переходим к построению эпюры касательных напряжений. Как было показано выше, максимальные касательные напряжения возникают в точках сечения, лежащих на линии 2 – 2
В точках сечения, лежащих на линиях 1 – 1 и 3 – 3, касательные напряжения равны 0
Используя полученные данные и учитывая, что касательные напряжения по высоте поперечного сечения изменяются по параболическому закону, строим эпюру касательных напряжений, как это показано на рис.6 Точки, лежащие на линии 2 – 2, являются опасными точками по касательным напряжениям.
6. Подбор круглого сечения деревянной балки по методу допускаемых напряжений (рис.7)
Момент сопротивления круга диаметром d определяется по формуле
Приравнивая Из полученного соотношения определяем размер d Рис.7 d Окончательно диаметр круглого сечения балки, с учетом технологических требований, принимаем d = 27, 5 cм. Проверим выполнение условия прочности. С этой целью определяем фактический момент сопротивления
Находим максимальное нормальное напряжение
Условие прочности выполняется.
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 2442; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.23.110 (0.007 с.) |

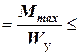 [ s ] (1)
[ s ] (1) - момент сопротивления относительно оси y;
- момент сопротивления относительно оси y; . (2)
. (2) .
.
 2000 см3.
2000 см3. Для прямоугольного поперечного сечения момент сопротивления выражается через размеры h и b (рис.5)
Для прямоугольного поперечного сечения момент сопротивления выражается через размеры h и b (рис.5) .
. .
. 2000 см3.
2000 см3. 12,4 35 cм=12,4 см.
12,4 35 cм=12,4 см.
 = 206 7,187 см3=2070 см3.
= 206 7,187 см3=2070 см3.
 1,15 94
1,15 94  11,6 МПа < [ s ]=12 МПа.
11,6 МПа < [ s ]=12 МПа. ,
,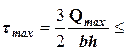 [ t ].
[ t ].  [ t ] =2МПа.
[ t ] =2МПа. 11,6 МПа.
11,6 МПа. –11,6 МПа.
–11,6 МПа.
 .
.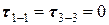 .
.
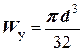 .
. .
.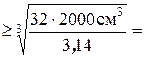 27,316 cм.
27,316 cм.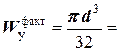
 204 0,69 см3=2040 см3.
204 0,69 см3=2040 см3. 1,17 6
1,17 6 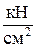 =11,8 МПа < 12 МПа.
=11,8 МПа < 12 МПа.


