
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет элементов нижнего пояса балкиСодержание книги Поиск на нашем сайте
Сечение 12, нормальное к продольной оси элемента (рис 5, а), N=1033,28 кН, М=23,08 кН·м. Расчет прочности выполняем согласно п. 3.50 [6]. Вычисляем эксцентриситет продольной силы:
Так как е0=22,3 мм<(h–ap')/2=(240–60)/2=90 мм, то продольная сила приложена между равнодействующими усилий в арматуре Sp и Sp', а эксцентриситеты соответственно равны:
По формулам (138) и (139) [6] находим требуемые площади сечения напрягаемой арматуры:
Принимаем 3Ø20 А-V, Asp. fact=942 мм2.
Asp. fact=509 мм2. Расчет трещиностойкости нижнего пояса балки выполняем на действие усилий от нормативных нагрузок, величины которых получим путем деления расчетных усилий на среднее значение коэффициента надёжности по нагрузке γfm=1,234. Для рассматриваемого сечения получим: усилия от суммарного действия постоянной и полного значения снеговой нагрузки:
усилие от постоянной и длительной части снеговой нагрузки
Согласно таблице 2 [2] нижний пояс фермы должен удовлетворять 3-й категории требований по трещиностойкости, т.е. допускается непродолжительное раскрытие трещин до 0,3 мм и продолжительное шириной до 0,2 мм. Вычисляем геометрические характеристики приведённого сечения по формулам (11) – (13) [4] и (168) – (175) [5]. Площадь приведенного сечения:
где: Статический момент приведенного сечения относительно нижней грани:
Момент инерции приведённого сечения:
Момент сопротивления приведённого сечения для нижней грани, наиболее растянутой от внешней нагрузки:
Упругопластический момент сопротивления сечения:
Определим первые потери предварительного натяжения арматуры по позиции 1–6 таблица 5 [2] для механического способа натяжения арматуры на упоры. Потери от релаксации напряжений в арматуре:
Потери от температурного перепада: Потери от деформации анкеров в виде инвентарных зажимов:
тогда Потери σ4 =0. Потери от деформации стальной формы отсутствуют, т.к. усилия обжатия передаются на упоры стенда, т.е. σ5=0. Напряжение в арматуре с учетом потерь по поз. 1–5 и соответственно условия обжатия будет равно:
Определим потери от быстронатекающей ползучести бетона, для чего вычисляем напряжения в бетоне на уровне арматур Sp и S’p, на уровне арматуры Sp (y = ysp =86мм)
На уровне арматуры
Соответственно потери напряжения при Rbp =20 МПа табл. 2.3 [8] будут равны: На уровне арматуры
на уровне арматуры Таким образом, первые потери и соответствующие напряжения в напрягаемой арматуре будут равны:
Соответственно получим напряжения в напрягаемой арматуре:
Определим усилие обжатия с учетом первых потерь и соответствующие напряжения в бетоне будет равно:
Проверим максимальные сжимающие напряжения от действия силы
Поскольку Определим вторые потери предварительного напряжения: потери от усадки легкого бетона равна: σ8= σ8’=45 МПа. Напряжения в бетоне от действия силы Р1 с эксцентриситетом Потери от ползучести бетона на уровне арматуры
То же для арматуры
Тогда вторые потери составят
а полные потери будут равны:
поэтому согласно п. 1.25. [2] потери не увеличиваем. Вычислим напряжения в напрягаемой арматуре с учетом полных потерь и соответствующее усилие обжатия:
Усилие обжатия с учетом суммарных потерь и его эксцентриситет соответственно составляют:
Проверку образования трещин выполняется по формуле п. 4.5 [2] для выяснения необходимости расчёта по ширине раскрытия трещин. Определим расстояние r от центра тяжести приведенного сечения до ядровой точки, наиболее удаленной от максимально растянутой внешней нагрузкой грани сечения. Поскольку N=837,34 кН >P2=477,3 кН·м, то значение тогда соответственно: Момент внешней продольной силы:
где: Поскольку Mcrc=61,567 кН·м < Mr=84,26 кН·м то трещины нормальные к продольной оси элемента нижнего пояса балки, образуются, и требуется расчёт по ширине их раскрытия.
Расчёт по раскрытию трещин выполняем в соответствии с требованиями пп.4.14 и 4.15 [2]. Определим величину равнодействующей Ntot и ее эксцентриситет относительно центра тяжести приведенного сечения:
Поскольку e0,tot=26,76 < 0,8h0=0,8·240=192 мм, то приращения напряжений в арматуре Sp вычисляем по формуле: от действия полной нагрузки:
=256,24 МПа. где: es=y0–ap–ео =146–60–22,3=63,7 мм. esp=y0–ap –еор2 =146–60–19=67 мм. zs=h0–a'p =240–60=180 мм. от действия длительной нагрузки:
=147,83 МПа. Вычислим ширину раскрытия трещин от непродолжительного действия полной нагрузки по формуле (144) [2]:
где: Вычислим ширину раскрытия трещин, от непродолжительного действия длительных нагрузок:
Вычислим ширину раскрытия трещин, от продолжительного действия длительных нагрузки (φl=1,5):
Таким образом, ширина непродолжительного раскрытия трещин от действия длительных и кратковременных нагрузок будет равна: acrc1=0,132–0,076+0,114=0,17 мм <[0,3] мм а ширина продолжительного раскрытия трещин в нижнем поясе фермы составит: acrc2=0,144 мм <[0,2] мм Следовательно, удовлетворяются требования к нижнему растянутому поясу балки по трещинностойкости. Выполняем расчёт прочности наклонного сечения нижнего пояса балки с учётом возможного перераспределения усилий между поясами в панели с сечениями 1, 2 и 9,10. Определим фактическую несущую способность нижнего пояса балки на действие поперечной силы, приняв поперечное армирование по конструктивным соображениям в виде замкнутых двухветвевых хомутов из арматуры диаметром 4 мм класса Вр–I с шагом Выполняем расчёт согласно п. 3.54 [2] с учётом действия продольной силы N=915,23кН и усилия обжатия от напрягаемой арматуры, расположенной в наиболее растянутой зоне: Определим коэффициент φn по формуле (149) [4]:
поскольку |φn|=1,64>0,8, принимаем φn= –0.8 Вычисляем значения Mb и qsw:
где φb2=1,75 (для лёгкого бетона по п. 3.31 [2]). Находим: где: φb3=0,4 по п. 3.31 [2]. Поскольку qsw=33,39 Н/мм>
Так как поперечная сила не меняется по длине элемента, то значение проекции наклонного сечения с может быть равной длине элемента (700 мм), но не более:
Тогда
Таким образом, предельная несущая способность нижнего пояса балки в наиболее опасном сечении будет равна Q=Qb+Qsw =8,986+14,494=23,48 кН, что меньше максимального значения поперечной силы от нагрузки Q=29,76. Следовательно, при расчёте прочности верхнего пояса балки на действие поперечной силы необходимо учесть дополнительное усилие ∆Q=29,76–23,48=6,28 кН.
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 419; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.147.12 (0.009 с.) |

 м=22,3 мм
м=22,3 мм мм;
мм; мм.
мм. мм2.
мм2. мм2, принимаем 2Ø18 А-V,
мм2, принимаем 2Ø18 А-V, кН,
кН,  кН·м;
кН·м;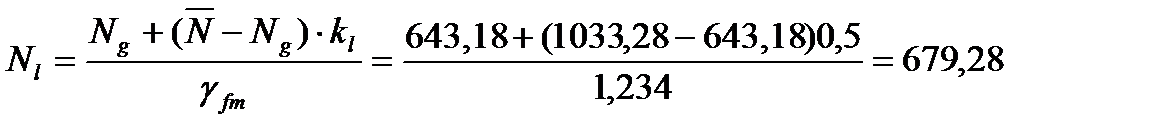 кН
кН кН·м.
кН·м. мм2.
мм2. .
. =1245,64∙104 мм3. Расстояние от нижней грани до центра тяжести приведенного сечения
=1245,64∙104 мм3. Расстояние от нижней грани до центра тяжести приведенного сечения  мм (рис 5, б).
мм (рис 5, б). мм4.
мм4. мм3.
мм3. мм3, где γ=1,75 (по табл. 38 [5])
мм3, где γ=1,75 (по табл. 38 [5]) МПа
МПа МПа.
МПа. мм и l=18+1=19 м.
мм и l=18+1=19 м. МПа
МПа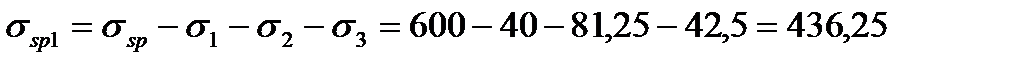 МПа
МПа кН.
кН. мм.
мм. МПа
МПа (y = ysp =94 мм)
(y = ysp =94 мм) МПа.
МПа. , принимаем α=0,75, поскольку
, принимаем α=0,75, поскольку  , то
, то МПа;
МПа; - при
- при  < α=0,75, то получаем
< α=0,75, то получаем 
 МПа.
МПа.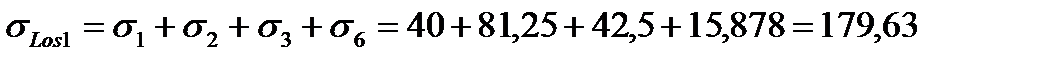 МПа;
МПа; МПа;
МПа; МПа;
МПа; МПа.
МПа. кН;
кН; мм.
мм. при y = yо =146 мм.
при y = yо =146 мм. МПа
МПа то требование табл. 7 [2] удовлетворяются.
то требование табл. 7 [2] удовлетворяются. на уровнях арматур
на уровнях арматур  соответственно будут равны
соответственно будут равны  МПа,
МПа,  МПа (вычисления опущены).
МПа (вычисления опущены). будет равны:
будет равны: МПа.
МПа. при
при  получим
получим МПа.
МПа.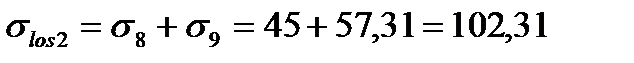 МПа;
МПа;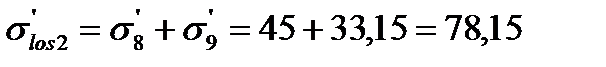 МПа.
МПа. МПа >100 МПа
МПа >100 МПа МПа >100 МПа
МПа >100 МПа МПа:
МПа: МПа.
МПа. кН.
кН. мм.
мм. определим по формуле:
определим по формуле:  мм.
мм. Н·мм=46,46 кН.
Н·мм=46,46 кН. кН·м.
кН·м. кН·м.
кН·м. мм.
мм. кН>0
кН>0 мм
мм
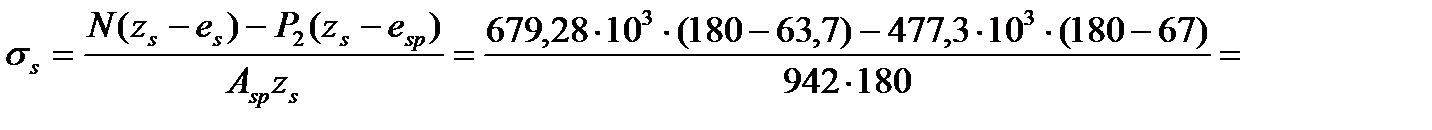
 , где: δ=1,2; φl=1; η=1 (для арматуры класса А-V) [2].
, где: δ=1,2; φl=1; η=1 (для арматуры класса А-V) [2]. , следовательно принимаем
, следовательно принимаем  0,02
0,02 мм
мм мм
мм 0,114мм.
0,114мм. мм (Asw=2·12,6=25,2 мм2, Rsw=265 МПа, Es=170000 МПа).
мм (Asw=2·12,6=25,2 мм2, Rsw=265 МПа, Es=170000 МПа). кН.
кН.
 кН·м.
кН·м. Н/мм
Н/мм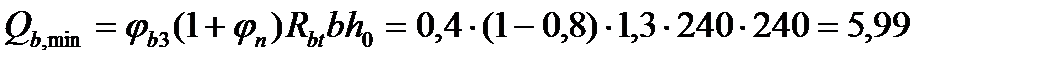 кН.
кН. Н/мм, то значение Mb не корректируем. Тогда длина проекции наклонной трещины будет равна:
Н/мм, то значение Mb не корректируем. Тогда длина проекции наклонной трещины будет равна: мм >2h0=2·240=480 мм. Принимаем с0=480 мм
мм >2h0=2·240=480 мм. Принимаем с0=480 мм мм. Принимаем с =700 мм.
мм. Принимаем с =700 мм. кН > Qb,min =5,99 кН
кН > Qb,min =5,99 кН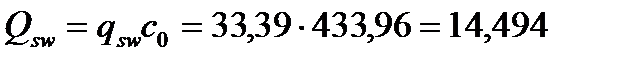 кН.
кН.


