Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Полная проверка прочности двутавровой балкиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
1) Проверка по нормальным напряжениям:
2) Проверка по касательным напряжениям:
3) Проверку по эквивалентным напряжениям выполним для сечения 7 (см. рис. 4.9), в котором действуют близкие к максимальным перерезывающая сила и изгибающий момент. Эквивалентные напряжения определим для точек а стенки в местах ее перехода в полки (см. рис. 4.7):
где статический момент площади полки
Эквивалентные напряжения в точках а по IV теории прочности
Для рассматриваемого опасного сечения построим эпюры распределения нормальных и касательных напряжений (рис. 4.11).
Касательные напряжения в полках в местах сопряжения со стенкой
а б
Рисунок 4.11 – Эпюры распределения нормальных (а) и касательных (б) напряжений в опасном поперечном сечении балки
Вопросы для самоконтроля
1 Какой вид нагружения называют чистым изгибом? 2 Какой вид нагружения называют поперечным изгибом? 3 Какой вид изгиба называют плоским? 4 Каковы принятые правила знаков для внутренних перерезывающих сил и изгибающих моментов? Почему знаки Qy и Mux определяют неих непосредственным направлением, а направлением деформаций, которые они вызывают? 5 Каковы основные правила проверки эпюр Qy и Mux на основе дифференциальных зависимостей между q, Qy и Mux? 6 Какие напряжения возникают в поперечном сечении балки от действия внутреннего изгибающего момента? 7 Какие напряжения возникают в поперечном сечении балки от действия внутренней перерезывающей силы? 8 Как выглядят формулы для s и t в поперечных сечениях балки при поперечном изгибе? 9 Каков закон распределения нормальных напряжений в поперечном сечении балки при изгибе? 10 Каков закон распределения касательных напряжений в поперечном сечении балки при поперечном изгибе? 11 В каких точках поперечного сечения возникают максимальные нормальные напряжения при изгибе? 12 В каких точках поперечного сечения возникают максимальные касательные напряжения при поперечном изгибе? 13 Какую величину называют осевым моментом инерции сечения? Какова его единица измерения? 14 Какую величину называют осевым моментом сопротивления сечения изгибу? Какова его единица измерения? 15 По какому условию прочности определяют сечения балок при поперечном изгибе и почему? 16Что понимают под эквивалентными напряжениями? 17 Почему для двутавровых сечений необходима проверка по эквивалентным напряжениям? СОВМЕСТНОЕ ДЕЙСТВИЕ КРУЧЕНИЯ С ИЗГИБОМ
Теоретические сведения
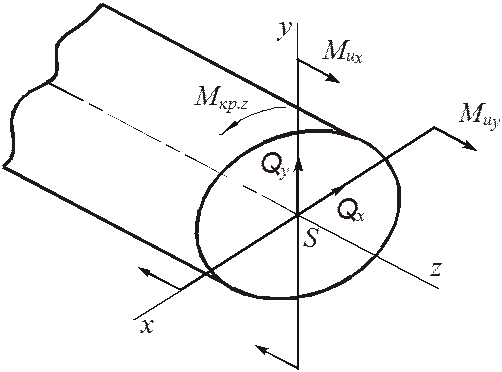
В разделе 3 рассматривается чистое кручение валов, но на практике кручение валов всегда сопровождается поперечным изгибом, в основном усилиями в насаженных на них элементах передач. В результате внутренние усилия в поперечных сечениях вала в общем случае приводятся к пяти силовым факторам: крутящему моменту Mкp.z, изгибающим моментам Mux и Muy и перерезывающим силам Qy и Qx (рис. 5.1).
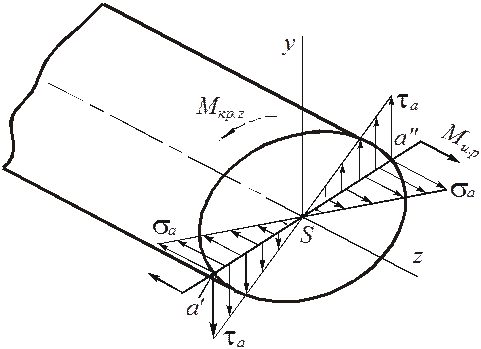
Рисунок 5.1 – Схема внутренних силовых факторов в поперечном сечении вала, работающего на кручение с изгибом Как правило, у валов касательные напряжения, возникающие от действия перерезывающих сил Qy и Qx, невелики и при расчетеих не учитывают. Поэтому расчет валов, работающих на кручение с изгибом, производят по трем внутренним силовым факторам: Mкp.z, Mux, Muy, которые вызывают в их поперечных сечениях нормальные напряжения s и касательные t (рис. 5.2).
Рисунок 5.2 – Распределение нормальных и касательных напряжений в поперечном сечении вала, работающего на кручение с изгибом Максимальные нормальные напряжения от изгиба в поперечном сечении вала возникают у его поверхности в осевой плоскости действия результирующего изгибающего момента Максимальные касательные напряжения в поперечном сечении вала также возникают у его поверхности. Таким образом, опасными будут точки a' и a". Элементарные параллелепипеды, выделенные в окрестности точек a' и a", находятся в условиях такого же плоского напряженного состояния, что и при поперечном изгибе (см. рис. 4.8), для которого эквивалентные напряжения по III и IV теориям прочности определяются формулами (4.7), (4.8). Разница состоит только в том, что при поперечном изгибе касательные напряжения вызваны не крутящим моментом, а перерезывающей силой. Для конкретного поперечного сечения вала нормальное и касательное напряжения в опасных точках:
Для сплошного поперечного сечения вала осевой и полярный моменты сопротивления сечения:
При этом для вала формулы (4.7), (4.8) принимают вид: - по III теории прочности
- по IV теории прочности
Здесь Мпр – приведенный момент. Можно считать что Мпр – это условный внутренний изгибающий момент в сечении, эквивалентный одновременно действующим в нем реальным внутренним изгибающему и крутящему моментам Мu.p и Мкр.z. При этом условие прочности вала, испытывающего одновременное действие кручения с изгибом,
где по III теории прочности (максимальных касательных напряжений)
по IV теории прочности (энергетической)
Для нахождения сечения c Mnp=Mnр.max необходимо предварительно построить эпюры Мu.p=f(Z) и Mкp.z=f(Z). При этом для построения эпюры Мu.p вначале должны быть построены эпюры Мux и Мuу. Понятно, что для каждого поперечного сечения вала результирующий момент Прежде чем строить указанные эпюры, необходимо составить расчетную схему вала, для чего все внешние силы, приложенные к насаженным на него элементам передач, должны быть перенесены на ось вала. Описанная методика расчета валов соответствует их статическому нагружению и может быть использована для проектировочных расчетов. Валы реальных передач круговращательного движения находятся в условиях переменного циклического нагружения. Поэтому для валов, конструктивно оформленных по найденному из проектировочного расчета диаметру, должен быть выполнен проверочный расчет на усталостную прочность (выносливость). При проектировочном статическом расчете неучтенную цикличность нагружения косвенно учитывают понижением допускаемого напряжения [ s ]. В некоторых конструкциях валы, помимо скручивания и изгиба, растягиваются или сжимаются осевыми нормальными силами N. Влияние этих добавочных сил на прочность вала может быть учтено добавкой к наибольшим нормальным напряжениям от изгиба Ввести sp в условие прочности проектировочного расчета (5.1) не представляется возможным, sp учитывают только при проверочных расчетах.
Пример расчета
Для заданной схемы нагружения промежуточного вала коническо-цилиндрического редуктора (рис. 5.3) определить необходимый диаметр вала, пользуясь теорией максимальных касательных напряжений. d1=200 мм; d2=100 мм; внешний крутящий момент, передаваемый валом Т=150 Hм; a=20º; δ=71,6º - углы между усилиями в зацеплениях; [ s ] =80 МПа.
Рисунок 5.3 – Схема нагружения вала
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 2748; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.124.80 (0.01 с.) |

 143 МПа< [ s ].
143 МПа< [ s ]. 76 МПа£ [ t ].
76 МПа£ [ t ].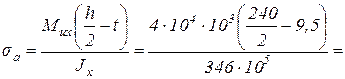 128 МПа;
128 МПа; 45 МПа,
45 МПа, мм3.
мм3. 149 МПа< [ s ].
149 МПа< [ s ].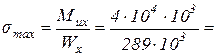 138 МПа;
138 МПа;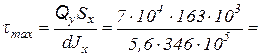 59 МПа.
59 МПа. 2,5 МПа.
2,5 МПа.
 – точки a' и a" (см. рис. 5.2).
– точки a' и a" (см. рис. 5.2). ;
;  .
.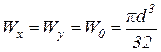 ;
;  , т. е. Wp = 2W0.
, т. е. Wp = 2W0. ;
;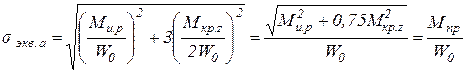 .
.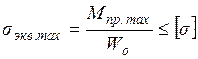 , (5.1)
, (5.1) ; (5.2)
; (5.2) . (5.3)
. (5.3) будет иметь свою осевую плоскость действия. Но так как вал имеет круглое поперечное сечение, для которого моменты сопротивления относительно всех осей одинаковы, то без влияния на результаты расчета можно построить условную эпюру Мu.р, совместив осевые плоскости действия результирующих изгибающих моментов во всех поперечных сечениях с плоскостью чертежа.
будет иметь свою осевую плоскость действия. Но так как вал имеет круглое поперечное сечение, для которого моменты сопротивления относительно всех осей одинаковы, то без влияния на результаты расчета можно построить условную эпюру Мu.р, совместив осевые плоскости действия результирующих изгибающих моментов во всех поперечных сечениях с плоскостью чертежа.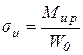 нормальных напряжений от растяжения-сжатия
нормальных напряжений от растяжения-сжатия  , где А - площадь поперечного сечения вала.
, где А - площадь поперечного сечения вала.