
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
К контрольным и расчетно-графическим работамСодержание книги Поиск на нашем сайте
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К КОНТРОЛЬНЫМ И РАСЧЕТНО-ГРАФИЧЕСКИМ РАБОТАМ ПО ДИСЦИПЛИНЕ «ПРИКЛАДНАЯ МЕХАНИКА И ОСНОВЫ КОНСТРУИРОВАНИЯ»
для специальностей «обработка металлов давлением» и «литейное производство»
Утверждено на заседании кафедры «Основы конструирования механизмов и машин»
Протокол № 4 от 10.12.02
Краматорск 2003 УДК 620.10
Методические указания к контрольным и расчетно-графическим работам по дисциплине «Прикладная механика и основы конструирования» (для студентов всех специальностей) / Сост.: С.Н. Зинченко, В.Л. Москаленко. – Краматорск: ДГМА, 2003. – 52 с.
В методуказаниях рассмотрены основные виды простых нагружений элементов конструкций: растяжение-сжатие, кручение, поперечный изгиб, совместное действие кручения с изгибом. Для каждого из перечисленных видов нагружений приведены изложенные в доступной форме теоретические основы, пример расчета и вопросы для самоконтроля. Указания являются пособием для самообразования и могут быть использованы студентами немеханических специальностей очной и заочной форм обучения, изучающим ПМиОК.
Составители: С.Н.Зинченко, доц., В.Л.Москаленко, ст. препод.
Отв. за выпуск С.Г.Карнаух, доц. СОДЕРЖАНИЕ 1 ОБЩИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ........................................................................ 4 2 РАСТЯЖЕНИЕ-СЖАТИЕ СТЕРЖНЕЙ............................................................................ 7 2.1 Теоретические сведения.............................................................................................. 7 2.2 Пример расчета.............................................................................................................. 10 2.3 Вопросы для самоконтроля......................................................................................... 12 3 КРУЧЕНИЕ ВАЛОВ............................................................................................................. 13 3.1 Теоретические сведения.............................................................................................. 13 3.1.1 Построение эпюры внутренних крутящих моментов...................................... 13 3.1.2 Деформации вала при кручении.......................................................................... 15 3.1.3 Напряжения в поперечных сечениях вала при кручении.............................. 15 3.1.4 Подбор сечений валов............................................................................................ 17
3.2 Пример расчета.............................................................................................................. 18 3.3 Вопросы для самоконтроля......................................................................................... 20 4 ПЛОСКИЙ ПОПЕРЕЧНЫЙ ИЗГИБ БАЛОК.................................................................. 21 4.1 Теоретические сведения.............................................................................................. 21 4.1.1 Определение реакций опор................................................................................... 21 4.1.2 Построение эпюр перерезывающих сил и изгибающих моментов.............. 22 4.1.3 Проверка правильности построения эпюр Qy и Мuх на основе дифференциальных зависимостей между q, Qy и Мuх........................................................................ 24 4.1.4 Напряжения в поперечных сечениях балки при поперечном изгибе......... 26 4.1.5 Подбор сечений балок........................................................................................... 29 4.2 Пример расчета.............................................................................................................. 31 4.2.1 Определение реакций опор.................................................................................. 31 4.2.2 Построение эпюр перерезывающих сил и изгибающих моментов............. 33 4.2.3 Анализ правильности построения эпюр перерезывающих сил и изгибающих моментов на основе дифференциальных зависимостей между q, Qy и Mux......... 34 4.2.4 Подбор сечений балки........................................................................................... 35 4.2.5 Полная проверка прочности двутавровой балки............................................. 37 4.3 Вопросы для самоконтроля......................................................................................... 38 5 СОВМЕСТНОЕ ДЕЙСТВИЕ КРУЧЕНИЯ С ИЗГИБОМ............................................... 40 5.1 Теоретические сведения.............................................................................................. 40 5.2 Пример расчета.............................................................................................................. 44 5.2.1 Определение расчетных нагрузок на вал.......................................................... 45 5.2.2 Изгиб вала в вертикальной плоскости............................................................... 46 5.2.3 Изгиб вала в горизонтальной плоскости........................................................... 47 5.2.4 Результирующие изгибающие моменты............................................................ 48 5.2.5 Построение эпюр внутренних крутящих моментов и нормальных сил..... 48 5.2.6 Определение диаметра вала................................................................................. 50 5.3 Вопросы для самоконтроля......................................................................................... 50 СПИСОК ЛИТЕРАТУРЫ....................................................................................................... 51
Рисунок 1.1 – Схема внутренних силовых факторов Отношение внутренней силы DR, приходящейся на элементарную площадку DA (рис. 1.2), к ее площади дает среднее напряжение на этой площадке:
Таким образом, напряжение Р – это внутреннее усилие, приходящееся на единицу площади в окрестности определенной точки рассматриваемого сечения. В СИ напряжение измеряется в мегапаскалях (ньютонах на квадратный миллиметр).
Рисунок 1.2 – Напряжения в поперечном сечении В общем случае напряжение Р составляет с площадкой DA некоторый угол a. При этом его раскладывают на две составляющие: одну - s, перпендикулярную площадке и называемую нормальным напряжением; вторую - t, лежащую в плоскости площадки и называемую касательным напряжением. В зависимости от того, какие из шести возможных внутренних силовых факторов(см. рис. 1.1) действуют в поперечных сечениях тела, производится классификация видов нагружения. В настоящем руководстве рассмотрены следующие виды нагружения бруса (тела, у которого длина значительно больше двух других размеров): растяжение-сжатие; кручение; поперечный изгиб; изгиб с кручением. Дисциплина «Сопротивление материалов» рассматривает только упругие деформации (исчезающие после снятия внешних нагрузок), для которых может быть использована гипотеза плоских сечений: плоские поперечные сечения бруса при деформации смещаются друг относительно друга, оставаясь плоскими. Эта гипотеза помогает представить закон распределения внутренних усилий (напряжений) по поперечному сечению бруса при различных его нагружениях. Указанные выше силовые факторы, действующие на поперечное сечение рассматриваемой части тела со стороны его отброшенной части (см. рис. 1.1), являются результирующими соответствующих напряжений (s и t) по этому сечению. РАСТЯЖЕНИЕ-СЖАТИЕ СТЕРЖНЕЙ
Теоретические сведения
Под растяжением-сжатием понимают такой вид нагружения бруса, при котором в любом его поперечном сечении из шести возможных внутренних силовых факторов (см. рис. 1.1) действует только один - нормальная сила N. На чистое растяжение-сжатие могут работать только прямолинейные брусья и только в том случае, если все действующие на брус внешние силы направлены строго по его оси. Брус, работающий на растяжение-сжатие, называют стержнем. Нормальная внутренняя сила в рассматриваемом поперечном сечении N – это результирующая напряжений, действующих по этому сечению. Следовательно, это нормальные напряжения s, которые при чистом растяжении-сжатии по поперечному сечению распределены равномерно, что следует из гипотезы плоских сечений:
где N - внутренняя нормальная сила в рассматриваемом поперечном сечении; А - площадь сечения. Для нахождения силы N в каком-то конкретном поперечном сечении нужно условно перевести ее из категории внутренних в категорию внешних, для чего стержень данным сечением нужно мысленно рассечь на две частии, отбросив одну из них, рассмотреть вторую. Нормальная сила N в поперечном сечении рассматриваемой части стержня представляет собой действие на нее отброшенной части и может быть найдена как сумма всех внешних сил, действующих на отброшенную часть:
Знак силы N определяют не ее направлением, а видом деформации, которую она вызывает. Принято деформацию растяжения считать положительной, а деформацию сжатия – отрицательной. Соответственно растягивающие силы N и напряжения растяжения – положительными, сжимающие силы N и напряжения сжатия – отрицательными.
Пусть требуется найти внутреннюю нормальную силу N в сечении n-n стержня, изображенного на рис. 2.1,а. Элемент dZ, выделенный у данного сечения будет находиться в равновесии только в том случае, если внутренние силы N, действующие на его боковые грани, будут обе направлены либо к граням (элемент dZ сжимается), либо от них (элемент dZ растягивается) – рис. 2.1,г. При этом при подстановке в уравнение (2.2) положительными должны считаться силы F, направленные от данного сечения, а отрицательными - направленные к сечению.

а – расчетная схема стержня; б – рассматриваемая часть стержня; в – отброшенная часть стержня; г – варианты нагружения элемента dZ Рисунок 2.1 – К определению внутренних нормальных сил при растяжении-сжатии В данном случае удобно рассмотреть левую часть стержня (рис. 2.1,б), а отбросить правую (рис. 2.1,в), что позволит определить силу N без нахождения реакции в опоре стержня
При этом сила F2 принята положительной, так как она направлена от рассматриваемого сечения, а сила F1 – отрицательной, так как она направлена к сечению. Согласно закону Гука абсолютное изменение длины участка стержня dz
где Е - модуль упругости материала стержня при растяжении-сжатии. Если в пределах какого-то участка стержня L N(Z)=N=const и A(Z)=A=const, абсолютное удлинение этого участка
Если материал стержня одинаково сопротивляется растяжению и сжатию, то условие прочности такого стержня на растяжение-сжатие имеет вид
где sпред - предельное напряжение для материала стержня; n - коэффициент запаса прочности (коэффициент безопасности). Для пластичных материалов (меди, алюминия, латуни, низкоуглеродистых сталей и др.) за предельное напряжение принимают предел текучести sТ; для хрупких (чугуна, высокоуглеродистых инструментальных сталей и др.) - предел прочности sпр. Коэффициент запаса прочности n зависит от многих причин: свойств материала, конкретных условий работы, соответствия нагрузок и расчетной схемы истинному нагружению, серьезности тех последствий, которые повлечет за собой разрушение, и т.д. Пример расчета
Для заданной схемы нагружения круглого стержня постоянного поперечногосечения (рис. 2.2) определить диаметр d, построить эпюры внутренних нормальных сил N и нормальных напряжений s и найти абсолютное удлинение DL.
а=0,5 м; в=0,75 м; с=0,5 м; F1=150 kH; F2=450 kH; F3=100 kH. Материал стержня - Ст.3; Е=2×105 МПа; sТ =240 МПа; n=1,5.
Рисунок 2.2 – Расчетная схема стержня и эпюры внутренних нормальных сил N и нормальных напряжений в поперечных сечениях σ 1) Определим внутренние нормальные силы N в поперечных сечениях стержня. При этом будем отбрасывать нижние части стержня, а рассматривать верхние: при 0 £ Z £ a: N=F1=150 kH; при a £ Z £ a+в: N=F1-F2=150–450=-300 kH; при a+в £ Z £ a+в+с: N=F1-F2+F3=150–450+100=-200 kH. 2) Необходимую площадь поперечного сечения стержня А определимизусловия прочности на растяжение-сжатие:
где Отсюда
Принимаем d=50 мм. Следует отметить, что округление значения геометрической характеристики сечения, полученного из условия прочности, можно выполнять только в большую сторону, так как в противном случае максимальные напряжения будут больше допускаемых.
3) Нормальные напряжения в поперечных сечениях стержня: при 0£ Z £ a: при a £ Z £ a+в: при a+в £ Z £ a+в+с: Эпюры N и s для участков стержня показаны на рис. 2.2. 4) Абсолютные удлинения участков стержня определим по формуле (2.4):
5) Полное абсолютное удлинение стержня
Вопросы для самоконтроля
1 Какое тело называют брусом? 2 Перечислить шесть возможных внутренних силовых факторов в поперечном сечении бруса. 3 Какой вид нагружения называют растяжением-сжатием? 4 Как определить внутреннюю нормальную силу в поперечном сечении стержня? 5 Что такое напряжение? 6 Какие напряжения называют нормальными, какие - касательными и какие деформации они вызывают? 7 Результирующей чего является внутренняя нормальная сила в поперечном сечении стержня? 8 Какие напряжения принимаются за предельные для хрупких, а какие - для пластичных материалов и почему? 9 Что такое допускаемое напряжение? 10 Что понимают под коэффициентом запаса прочности? 11 Какие напряжения возникают в поперечных, продольных и наклонных сечениях бруса, работающего на растяжение-сжатие? 12 Как выглядит условие прочности стержня при чистом растяжении-сжатии?
КРУЧЕНИЕ ВАЛОВ
Теоретические сведения
Под кручением понимают такой вид нагружения бруса, при котором в любом его поперечном сечении из шести возможных внутренних силовых факторов (см. рис. 1.1) действует только один - крутящий момент вокруг продольной оси Мкр.z. Будем рассматривать кручение брусьев круглого поперечного сечения, называемых валами.
Подбор сечений валов
Для обеспечения надежной работы валы должны удовлетворять условию прочности и условию жесткости. Для валов, работающих на чистое кручение, условие прочности имеет вид
где [ t ] - допускаемое касательное напряжение для материала вала. Отсюда полярный момент сопротивления сечения, удовлетворяющий условию прочности:
Валы на чистое кручение никогда не работают, так как всегда кроме кручения испытывают изгиб от собственной силы тяжести, сил тяжести насаженных на него элементов передач и усилий в этих передачах. Однако даже при значительных изгибных нагрузках, при приближенных прикидочных расчетах валы считают работающими на чистое кручение, а действие изгиба косвенно учитывают путем понижения допускаемого напряжения [ t ].
Пример расчета
На передаточный вал сплошного круглого постоянного поперечного сечения (рис. 3.2,a) насажены четыре шкива. Шкив С получает от двигателя внешний крутящий момент mС. Шкивы А, В, Д входят в ременные передачи, вторые шкивы которых насажены на три вала, параллельные рассматриваемому, со стороны которых он через эти шкивы получает внешние моменты mA, mB, mД. Три из четырех указанных моментов известны по величине и направлению, четвертый – неизвестен ни по величине, ни по направлению. mС=2100 Нм; mA=600 Нм; mД=800 Нм; G=8×104 МПа; [ τ ] =20 МПа; [ θ ] =0,25 Для заданного вала построить эпюру внутренних крутящих моментов и определить диаметр, обеспечивающий его прочность и жесткость.

Рисунок 3.2 – Расчетная схема вала и эпюра внутренних крутящих моментов Мкр.z 1) Определим внешний момент mB, для чего используем уравнение равновесия вала (3.2). Будем смотреть на вал слева, считая положительным направление m против часовой стрелки. Искомый момент mB предварительно направим против часовой стрелки. Моментами трения в опорах вала будем пренебрегать. ΣmZ = mА + mВ - mС + mД = 0; mВ = -mА + mС - mД = - 600 + 2100 - 800 = 700 Нм. Знак искомого момента mВ получился положительным, следовательно, его направление было выбрано верно. 2) Определим внутренние крутящие моменты в поперечных сечениях участков вала, используя указанное выше правило знаков (см. стр. 14). При этом будем перемещаться вдоль вала слева направо, отбрасывая левые и рассматривая правые его части. При 0 £ Z £ 0,2 м: Мкр.z=mА=600 Нм. При 0,2 м £ Z £ 0,5 м: Мкр.z=mА+mВ=600+700=1300 Нм. При 0,5 м £ Z £ 0,9 м: Мкр.z=mА+mВ-mС=600+700–2100=-800 Нм. Проверим последнее значение Мкр.z ходом справа налево: При 0 £ Z £ 0,4 м: Мкр.z=-mД=-800 Нм. Эпюра Мкр.z показана на рис. 3.2,б. 3) Определим диаметр вала, обеспечивающий условие его прочности:
Для сплошного вала Wp= Отсюда С целью приведения в соответствие размерностей числителя и знаменателя выражения для d значение момента Мкр.max подставляем в него в Н×мм. 4) Определим диаметр вала, обеспечивающий условие жесткости
Для сплошного вала Jp= Отсюда где Окончательно принимаем d=80 мм. 5) Проверим прочность и жесткость рассматриваемого вала при d=80 мм.
где
где
Вопросы для самоконтроля 1 Какой вид нагружения называют кручением? 2 В каких случаях вал будет работать начистоекручение? 3 Как по передаваемой мощности определить соответствующий крутящий момент? 4 Какую величину называют полярным моментом инерции сечения? Какова его единица измерения? 5 Какую величину называют полярным моментом сопротивления сечения? Какова его единица измерения? 6Что такое относительный угол закручивания? 7 Как распределяются касательные напряжения по поперечному сечению вала при кручении? 8 В каких точках вала возникают наибольшие касательные напряжения при кручении? 9 Как выглядит условие прочности вала при кручении? 10 Как выглядит условие жесткости вала при кручении? 11 Какие напряжения возникают в поперечных, продольных и наклонных сечениях вала при кручении? 12 В чем заключается закон парности касательных напряжений? Теоретические сведения
Под изгибом понимают такой вид нагружения бруса, при котором в его поперечных сечениях из шести возможных внутренних силовых факторов действуют только изгибающие моменты или изгибающие моменты и перерезывающие силы (см. рис. 1.1). Если изгибающие моменты в сечениях являются единственными факторами, изгиб называют чистым. В большинстве случаев в поперечных сечениях бруса наряду с изгибающими моментами действуют и перерезывающие силы. В этом случае изгиб называют поперечным. Брус, работающий на изгиб, называют балкой. Следует иметь в виду, что при изгибе все внешние силы, которые включают и реакции опор, должны быть перпендикулярны оси балки, так как в противном случае к изгибу добавилось бы растяжение-сжатие. Будем рассматривать прямолинейные балки постоянного поперечного сечения, имеющие продольную плоскость симметрии и нагруженные внешними силами и моментами, лежащими в этой плоскости. В данном случае продольная ось балки, находящаяся в силовой плоскости до изгиба, и в изогнутом состоянии будет находиться в этой же плоскости. Такой вид изгиба называют плоским.
Определение реакций опор
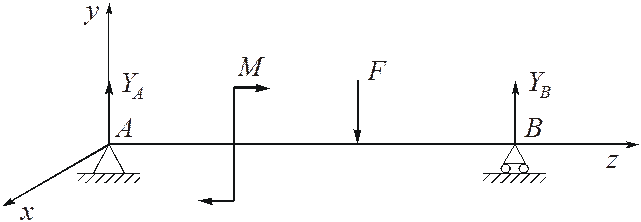
Пусть силовой плоскостью, совпадающей с продольной плоскостью симметрии балки, будет плоскость YZ, где Z – продольная ось балки (рис. 4.1). При этом нейтральный слой балки (слой продольных волокон, которые при изгибе искривляются, не изменяя своей длины) – XZ. B этом случае реакции опор будут иметь только составляющие, параллельные оси Y, которые могут быть найдены из уравнений равновесия:
Рисунок 4.1 – Пример балки, работающей на изгиб в плоскости YZ
Удобно реакции находить из первых двух уравнений (4.1), а третье использовать для проверки их правильности. При составлении уравнений моментов за положительное направление может быть принято любое, как по часовой стрелке, так и против. Направлением неизвестных реакций удобно предварительно задаться. Полученные при решении уравнений знаки укажутихистинные направления. Плюс будет говорить о том, что направление выбрано верно, минус - о том, что истинное направление реакции противоположно выбранному.
Подбор сечений балок
Для большинства встречающихся на практике длинных балок нормальные напряжения значительно выше касательных, поэтому необходимое сечение балок, как правило, находят из условия прочности по нормальным напряжениям, которое для материалов, одинаково сопротивляющихся растяжению и сжатию, имеет вид
Сечение, полученное из условия прочности (4.6), проверяют по касательным напряжениям (
а – точки стенки в месте перехода её в полки Рисунок 4.7 – Эпюры распределения σ и τ в двутавровом сечении при поперечном изгибе В окрестности точки а (см. рис. 4.7) плоскостями, параллельными координатным, выделим элемент в виде бесконечно малого прямоугольного параллелепипеда (рис. 4.8). По боковым граням этого элемента будут действовать напряжения sa и ta. Согласно закону парности касательные напряжения, равные по величине ta, будут действовать также по верхней и нижней его граням. Нормальные напряжения по этим граням для поперечных сечений, взятых на достаточном удалении от внешних сил, будут равны нулю. Две грани (передняя и задняя) свободны от напряжений. Таким образом, выделенный элемент испытывает плоское напряженное состояние.
Рисунок 4.8 – К определению эквивалентных напряжений при поперечном изгибе
Для данного вида плоского напряженного состояния по III теории прочности (максимальных касательных напряжений)
по IV теории прочности (энергетической)
Можно считать, что в рассматриваемом случае sэкв - это условное нормальное напряжение в рассматриваемой точке сечения, которое в ее окрестности создает напряженное состояние равноопасное тому, которое создают одновременно реально действующие в ней s и t.
Пример расчета
Для заданной схемы балки (рис. 4.9) построить эпюры внутренних перерезывающих сил и изгибающих моментов. Из условия прочности балки по нормальным напряжениям подобрать круглое, прямоугольное (с отношением h/b=2) и двутавровое сечения. Для наиболее экономичного сечения произвести полную проверку балки на прочность. Материал балки – Ст. 3. [ σ ] =160 МПа; [ τ ] =100 МПа. Определение реакций опор
Проверка:
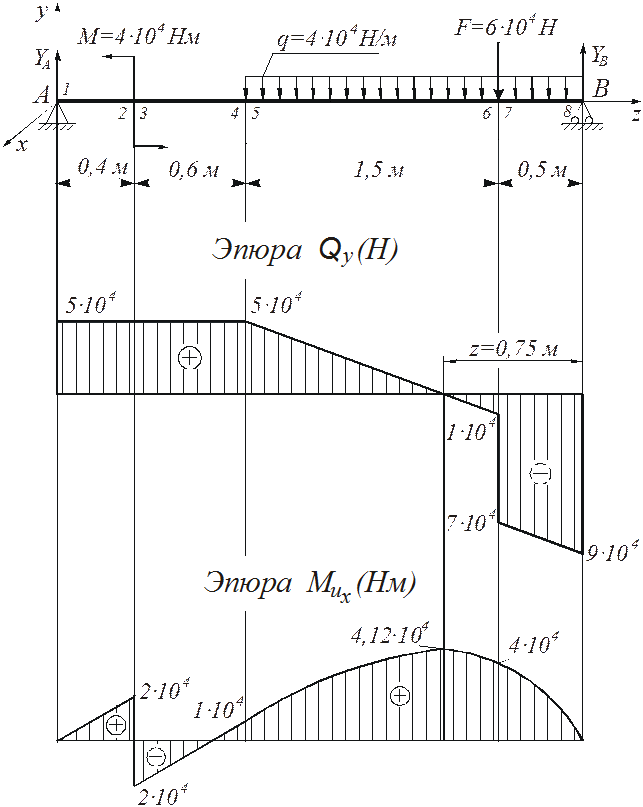
Рисунок 4.9 – Расчетная схема балки (а) и эпюры перерезывающих сил (б) и изгибающих моментов (в) Подбор сечений балки
Сечения балки подбираем из условия прочности по нормальным напряжениям, формула (4.6)
Отсюда 1) Круглое сечение: Wx»
2) Прямоугольное сечение (h=2b):
3) Двутавровое сечение: По сортаменту ГОСТ 8239-89 выбираем двутавр № 24 с Wx=289×103 мм3 и Ад=3,48×103 мм2. Площади полученных поперечных сечений относятся: Ад: Аn: Aк = 3,48×103: 10,6×103: 14,7×103 = 1: 3,04: 4,22. Таким образом, наименьшую площадь имеет двутавровое сечение, а наибольшую - круглое. При одинаковых удельных массах и длинах массы рассмотренных вариантов балок будут относиться как площади поперечных сечений. Следовательно, самым экономичным с точки зрения расхода материала будет двутавровое сечение, поэтому окончательно для рассматриваемой балки принимаем двутавровое сечение. Берем двутавр №24 (рис. 4.10), для которого:
h=240 мм; b=115 мм; t=9,5 мм; d=5,6 мм. Здесь Sx - статический момент половины сечения двутавра относительно нейтральной оси х–х.
Рисунок 4.10 – Схема сечения двутавра Вопросы для самоконтроля
1 Какой вид нагружения называют чистым изгибом? 2 Какой вид нагружения называют поперечным изгибом? 3 Какой вид изгиба называют плоским? 4 Каковы принятые правила знаков для внутренних перерезывающих сил и изгибающих моментов? Почему знаки Qy и Mux определяют неих непосредственным направлением, а направлением деформаций, которые они вызывают? 5 Каковы основные правила проверки эпюр Qy и Mux на основе дифференциальных зависимостей между q, Qy и Mux? 6 Какие напряжения возникают в поперечном сечении балки от действия внутреннего изгибающего момента? 7 Какие напряжения возникают в поперечном сечении балки от действия внутренней перерезывающей силы? 8 Как выглядят формулы для s и t в поперечных сечениях балки при поперечном изгибе? 9 Каков закон распределения нормальных напряжений в поперечном сечении балки при изгибе? 10 Каков закон распределения касательных напряжений в поперечном сечении балки при поперечном изгибе? 11 В каких точках поперечного сечения возникают максимальные нормальные напряжения при изгибе? 12 В каких точках поперечного сечения возникают максимальные касательные напряжения при поперечном изгибе? 13 Какую величину называют осевым моментом инерции сечения? Какова его единица измерения? 14 Какую величину называют осевым моментом сопротивления сечения изгибу? Какова его единица измерения? 15 По какому условию прочности определяют сечения балок при поперечном изгибе и почему? 16Что понимают под эквивалентными напряжениями? 17 Почему для двутавровых сечений необходима проверка по эквивалентным напряжениям? Теоретические сведения
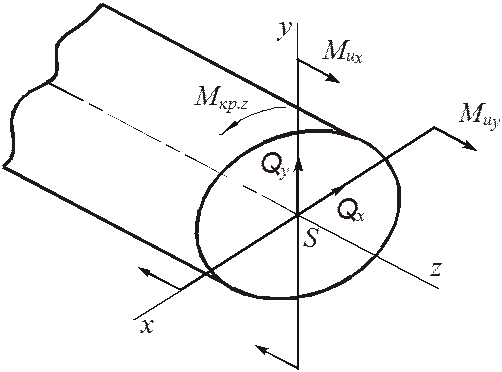
В разделе 3 рассматривается чистое кручение валов, но на практике кручение валов всегда сопровождается поперечным изгибом, в основном усилиями в насаженных на них элементах передач. В результате внутренние усилия в поперечных сечениях вала в общем случае приводятся к пяти силовым факторам: крутящему моменту Mкp.z, изгибающим моментам Mux и Muy и перерезывающим силам Qy и Qx (рис. 5.1).
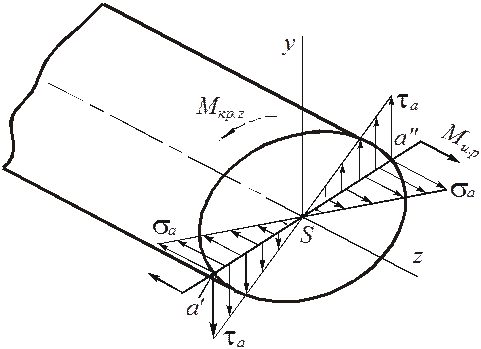
Рисунок 5.1 – Схема внутренних силовых факторов в поперечном сечении вала, работающего на кручение с изгибом Как правило, у валов касательные напряжения, возникающие от действия перерезывающих сил Qy и Qx, невелики и при расчетеих не учитывают. Поэтому расчет валов, работающих на кручение с изгибом, производят по трем внутренним силовым факторам: Mкp.z, Mux, Muy, которые вызывают в их поперечных сечениях нормальные напряжения s и касательные t (рис. 5.2).
Рисунок 5.2 – Распределение нормальных и касательных напряжений в поперечном сечении вала, работающего на кручение с изгибом Максимальные нормальные напряжения от изгиба в поперечном сечении вала возникают у его поверхности в осевой плоскости действия результирующего изгибающего момента Максимальные касательные напряжения в поперечном сечении вала также возникают у его поверхности. Таким образом, опасными будут точки a' и a". Элементарные параллелепипеды, выделенные в окрестности точек a' и a", находятся в условиях такого же плоского напряженного состояния, что и при поперечном изгибе (см. рис. 4.8), для которого эквивалентные напряжения по III и IV теориям прочности определяются формулами (4.7), (4.8). Разница состоит только в том, что при поперечном изгибе касательные напряжения вызваны не крутящим моментом, а перерезывающей силой. Для конкретного поперечного сечения вала нормальное и касательное напряжения в опасных точках:
Для сплошного поперечного сечения вала осевой и полярный моменты сопротивления сечения:
При этом для вала формулы (4.7), (4.8) принимают вид: - по III теории прочности
- по IV теории прочности
Здесь Мпр – приведенный момент. Можно считать что Мпр – это условный внутренний изгибающий момент в сечении, эквивалентный одновременно действующим в нем реальным внутренним изгибающему и крутящему моментам Мu.p и Мкр.z. При этом условие прочности вала, испытывающего одновременное действие кручения с изгибом,
где по III теории прочности (максимальных касательных напряжений)
по IV теории прочности (энергетической)
Для нахождения сечения c Mnp=Mnр.max необходимо предварительно построить эпюры Мu.p=f(Z) и Mкp.z=f(Z). При этом для построения эпюры Мu.p вначале должны быть построены эпюры Мux и Мuу. Понятно, что для каждого поперечного сечения вала результирующий момент Прежде чем строить указанные эпюры, необходимо составить расчетную схему вала, для чего все внешние силы, приложенные к насаженным на него элементам передач, должны быть перенесены на ось вала. Описанная методика расчета валов соответствует их статическому нагружению и может быть использована для проектировочных расчетов. Валы реальных передач круговращательного движения находятся в условиях переменного циклического нагружения. Поэтому для валов, конструктивно оформленных
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 607; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.8.172 (0.018 с.) |

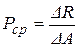 .
.
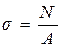 , (2.1)
, (2.1)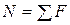 . (2.2)
. (2.2) .
. , (2.3)
, (2.3) . (2.4)
. (2.4) , (2.5)
, (2.5) - допускаемое нормальное напряжение для материала стержня;
- допускаемое нормальное напряжение для материала стержня;
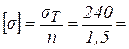 160 МПа.
160 МПа. мм2.
мм2. При этом
При этом  мм.
мм. мм2.
мм2. МПа< [ s ];
МПа< [ s ]; -153 МПа< [ s ];
-153 МПа< [ s ]; -102 МПа< [ s ].
-102 МПа< [ s ].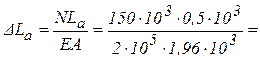 0,15 мм;
0,15 мм; мм;
мм; мм.
мм.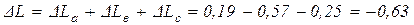 мм.
мм. , ( 3. 10 )
, ( 3. 10 ) .
. .
. .
.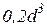 .
.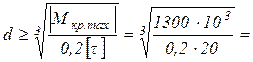 69 мм.
69 мм. .
. .
. 78 мм,
78 мм,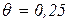
 =
= 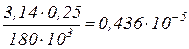
 .
. 12,7 МПа< [ t ],
12,7 МПа< [ t ], мм3.
мм3.
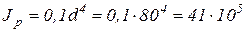 мм4.
мм4.
 (4.1)
(4.1) .
.
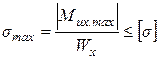 . (4.6)
. (4.6) ). Проверка эта делается для сечения с максимальной перерезывающей силой. Для тонкостенных (тавровых, двутавровых и коробчатых) балок делается дополнительная проверка по эквивалентным напряжениям (
). Проверка эта делается для сечения с максимальной перерезывающей силой. Для тонкостенных (тавровых, двутавровых и коробчатых) балок делается дополнительная проверка по эквивалентным напряжениям ( ) для точек стенки в месте их перехода в полку, где одновременно могут быть значительными как нормальные, так и касательные напряжения (рис. 4.7). Проверка эта делается для сечений, где одновременно действуют большие внутренние изгибающий момент и перерезывающая сила.
) для точек стенки в месте их перехода в полку, где одновременно могут быть значительными как нормальные, так и касательные напряжения (рис. 4.7). Проверка эта делается для сечений, где одновременно действуют большие внутренние изгибающий момент и перерезывающая сила.

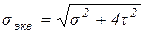 ; (4.7)
; (4.7) . (4.8)
. (4.8) :
:  ;
; Н.
Н. :
: 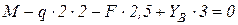 ;
; Н.
Н. :
: 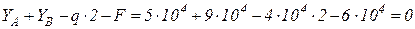 .
.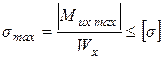 .
. мм3.
мм3. ;
;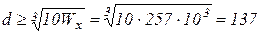 мм;
мм; мм2.
мм2. ;
; мм;
мм;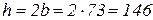 мм;
мм; мм2.
мм2. мм4;
мм4; мм3;
мм3;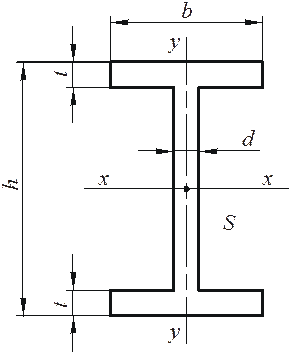
 – точки a' и a" (см. рис. 5.2).
– точки a' и a" (см. рис. 5.2). ;
;  .
.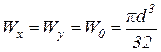 ;
;  , т. е. Wp = 2W0.
, т. е. Wp = 2W0. ;
;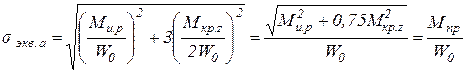 .
.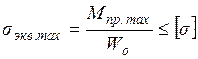 , (5.1)
, (5.1) ; (5.2)
; (5.2) . (5.3)
. (5.3) будет иметь свою осевую плоскость действия. Но так как вал имеет круглое поперечное сечение, для которого моменты сопротивления относительно всех осей одинаковы, то без влияния на результаты расчета можно построить условную эпюру Мu.р, совместив осевые плоскости действия результирующих изгибающих моментов во всех поперечных сечениях с плоскостью чертежа.
будет иметь свою осевую плоскость действия. Но так как вал имеет круглое поперечное сечение, для которого моменты сопротивления относительно всех осей одинаковы, то без влияния на результаты расчета можно построить условную эпюру Мu.р, совместив осевые плоскости действия результирующих изгибающих моментов во всех поперечных сечениях с плоскостью чертежа.


