
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие Теоретические сведенияСодержание книги Поиск на нашем сайте
При нагружении тела внешними силами между его элементарными (бесконечно малыми) площадками возникают дополнительные внутренние силы взаимодействия, являющиеся непосредственной причиной нарушения целостности материала по этим площадкам, которое может происходить за счет их отрыва (вмятия) и за счет сдвига. Для определения указанных сил их из класса внутренних нужно условно перевести в класс внешних, т.е. выявить. Достигается это методом сечений. Тело условно рассекается рассматриваемым сечением на две части, одна из которых отбрасывается, а вторая рассматривается. При этом для нахождения внутренних сил рассматривать можно любую часть тела, находящуюся как по одну, так и по другую сторону от сечения, так как согласно третьему закону Ньютона действие равно противодействию. Рассматриваемая часть должна находиться в равновесии под действием приложенных к ней внешних сил и системы внутренних (играющих для нее роль внешних), выражающих действие отброшенной части и распределенных по всему сечению. Закон распределения внутренних сил по сечению в общем случае неизвестен. Будучи приведена к центру тяжести S рассматриваемого сечения, система действующих по нему внутренних сил приводится к главному вектору Так как указанные силовые факторы в сечении рассматриваемой части тела выражают действие на нее отброшенной части, они могут быть найдены как сумма соответствующих внешних сил и моментов (илиих проекций), действующих на отброшенную часть. При этом следует иметь в виду, что в число внешних сил должны входить и реакции опор. Чтобы, независимо от того, какая часть тела рассматривается, а какая отбрасывается, внутренние силовые факторы получались одинаковыми не только по величине, но и по знаку, знаки указанных факторов определяют не их непосредственным направлением, а направлением или видом деформации, которую они вызывают. Соответствующие правила знаков внутренних силовых факторов приведены ниже.
N – нормальная сила; Qx, Qy – перерезывающие силы; Mux, Muy – изгибающие моменты; Mкp.z – крутящий момент вокруг оси Z Рисунок 1.1 – Схема внутренних силовых факторов Отношение внутренней силы DR, приходящейся на элементарную площадку DA (рис. 1.2), к ее площади дает среднее напряжение на этой площадке:
Таким образом, напряжение Р – это внутреннее усилие, приходящееся на единицу площади в окрестности определенной точки рассматриваемого сечения. В СИ напряжение измеряется в мегапаскалях (ньютонах на квадратный миллиметр).
Рисунок 1.2 – Напряжения в поперечном сечении В общем случае напряжение Р составляет с площадкой DA некоторый угол a. При этом его раскладывают на две составляющие: одну - s, перпендикулярную площадке и называемую нормальным напряжением; вторую - t, лежащую в плоскости площадки и называемую касательным напряжением. В зависимости от того, какие из шести возможных внутренних силовых факторов(см. рис. 1.1) действуют в поперечных сечениях тела, производится классификация видов нагружения. В настоящем руководстве рассмотрены следующие виды нагружения бруса (тела, у которого длина значительно больше двух других размеров): растяжение-сжатие; кручение; поперечный изгиб; изгиб с кручением. Дисциплина «Сопротивление материалов» рассматривает только упругие деформации (исчезающие после снятия внешних нагрузок), для которых может быть использована гипотеза плоских сечений: плоские поперечные сечения бруса при деформации смещаются друг относительно друга, оставаясь плоскими. Эта гипотеза помогает представить закон распределения внутренних усилий (напряжений) по поперечному сечению бруса при различных его нагружениях. Указанные выше силовые факторы, действующие на поперечное сечение рассматриваемой части тела со стороны его отброшенной части (см. рис. 1.1), являются результирующими соответствующих напряжений (s и t) по этому сечению. РАСТЯЖЕНИЕ-СЖАТИЕ СТЕРЖНЕЙ
Теоретические сведения
Под растяжением-сжатием понимают такой вид нагружения бруса, при котором в любом его поперечном сечении из шести возможных внутренних силовых факторов (см. рис. 1.1) действует только один - нормальная сила N. На чистое растяжение-сжатие могут работать только прямолинейные брусья и только в том случае, если все действующие на брус внешние силы направлены строго по его оси. Брус, работающий на растяжение-сжатие, называют стержнем. Нормальная внутренняя сила в рассматриваемом поперечном сечении N – это результирующая напряжений, действующих по этому сечению. Следовательно, это нормальные напряжения s, которые при чистом растяжении-сжатии по поперечному сечению распределены равномерно, что следует из гипотезы плоских сечений:
где N - внутренняя нормальная сила в рассматриваемом поперечном сечении; А - площадь сечения. Для нахождения силы N в каком-то конкретном поперечном сечении нужно условно перевести ее из категории внутренних в категорию внешних, для чего стержень данным сечением нужно мысленно рассечь на две частии, отбросив одну из них, рассмотреть вторую. Нормальная сила N в поперечном сечении рассматриваемой части стержня представляет собой действие на нее отброшенной части и может быть найдена как сумма всех внешних сил, действующих на отброшенную часть:
Знак силы N определяют не ее направлением, а видом деформации, которую она вызывает. Принято деформацию растяжения считать положительной, а деформацию сжатия – отрицательной. Соответственно растягивающие силы N и напряжения растяжения – положительными, сжимающие силы N и напряжения сжатия – отрицательными. Пусть требуется найти внутреннюю нормальную силу N в сечении n-n стержня, изображенного на рис. 2.1,а. Элемент dZ, выделенный у данного сечения будет находиться в равновесии только в том случае, если внутренние силы N, действующие на его боковые грани, будут обе направлены либо к граням (элемент dZ сжимается), либо от них (элемент dZ растягивается) – рис. 2.1,г. При этом при подстановке в уравнение (2.2) положительными должны считаться силы F, направленные от данного сечения, а отрицательными - направленные к сечению.

а – расчетная схема стержня; б – рассматриваемая часть стержня; в – отброшенная часть стержня; г – варианты нагружения элемента dZ Рисунок 2.1 – К определению внутренних нормальных сил при растяжении-сжатии В данном случае удобно рассмотреть левую часть стержня (рис. 2.1,б), а отбросить правую (рис. 2.1,в), что позволит определить силу N без нахождения реакции в опоре стержня
При этом сила F2 принята положительной, так как она направлена от рассматриваемого сечения, а сила F1 – отрицательной, так как она направлена к сечению. Согласно закону Гука абсолютное изменение длины участка стержня dz
где Е - модуль упругости материала стержня при растяжении-сжатии. Если в пределах какого-то участка стержня L N(Z)=N=const и A(Z)=A=const, абсолютное удлинение этого участка
Если материал стержня одинаково сопротивляется растяжению и сжатию, то условие прочности такого стержня на растяжение-сжатие имеет вид
где sпред - предельное напряжение для материала стержня; n - коэффициент запаса прочности (коэффициент безопасности). Для пластичных материалов (меди, алюминия, латуни, низкоуглеродистых сталей и др.) за предельное напряжение принимают предел текучести sТ; для хрупких (чугуна, высокоуглеродистых инструментальных сталей и др.) - предел прочности sпр. Коэффициент запаса прочности n зависит от многих причин: свойств материала, конкретных условий работы, соответствия нагрузок и расчетной схемы истинному нагружению, серьезности тех последствий, которые повлечет за собой разрушение, и т.д. Пример расчета
Для заданной схемы нагружения круглого стержня постоянного поперечногосечения (рис. 2.2) определить диаметр d, построить эпюры внутренних нормальных сил N и нормальных напряжений s и найти абсолютное удлинение DL. а=0,5 м; в=0,75 м; с=0,5 м; F1=150 kH; F2=450 kH; F3=100 kH. Материал стержня - Ст.3; Е=2×105 МПа; sТ =240 МПа; n=1,5.
Рисунок 2.2 – Расчетная схема стержня и эпюры внутренних нормальных сил N и нормальных напряжений в поперечных сечениях σ 1) Определим внутренние нормальные силы N в поперечных сечениях стержня. При этом будем отбрасывать нижние части стержня, а рассматривать верхние: при 0 £ Z £ a: N=F1=150 kH; при a £ Z £ a+в: N=F1-F2=150–450=-300 kH; при a+в £ Z £ a+в+с: N=F1-F2+F3=150–450+100=-200 kH. 2) Необходимую площадь поперечного сечения стержня А определимизусловия прочности на растяжение-сжатие:
где Отсюда
Принимаем d=50 мм. Следует отметить, что округление значения геометрической характеристики сечения, полученного из условия прочности, можно выполнять только в большую сторону, так как в противном случае максимальные напряжения будут больше допускаемых.
3) Нормальные напряжения в поперечных сечениях стержня: при 0£ Z £ a: при a £ Z £ a+в: при a+в £ Z £ a+в+с: Эпюры N и s для участков стержня показаны на рис. 2.2. 4) Абсолютные удлинения участков стержня определим по формуле (2.4):
5) Полное абсолютное удлинение стержня
Вопросы для самоконтроля
1 Какое тело называют брусом? 2 Перечислить шесть возможных внутренних силовых факторов в поперечном сечении бруса. 3 Какой вид нагружения называют растяжением-сжатием? 4 Как определить внутреннюю нормальную силу в поперечном сечении стержня? 5 Что такое напряжение? 6 Какие напряжения называют нормальными, какие - касательными и какие деформации они вызывают? 7 Результирующей чего является внутренняя нормальная сила в поперечном сечении стержня? 8 Какие напряжения принимаются за предельные для хрупких, а какие - для пластичных материалов и почему? 9 Что такое допускаемое напряжение? 10 Что понимают под коэффициентом запаса прочности? 11 Какие напряжения возникают в поперечных, продольных и наклонных сечениях бруса, работающего на растяжение-сжатие? 12 Как выглядит условие прочности стержня при чистом растяжении-сжатии?
КРУЧЕНИЕ ВАЛОВ
Теоретические сведения
Под кручением понимают такой вид нагружения бруса, при котором в любом его поперечном сечении из шести возможных внутренних силовых факторов (см. рис. 1.1) действует только один - крутящий момент вокруг продольной оси Мкр.z. Будем рассматривать кручение брусьев круглого поперечного сечения, называемых валами.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 562; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.83.96 (0.01 с.) |

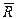 , приложенному к точке S, и главному моменту
, приложенному к точке S, и главному моменту  , действующему в некоторой плоскости, проходящей через S. Если выбрать прямоугольную систему координат ХYZ с центром в S, расположив оси X и Y в плоскости сечения, а ось Z -перпендикулярно ему, и спроектировать на указанные оси векторы
, действующему в некоторой плоскости, проходящей через S. Если выбрать прямоугольную систему координат ХYZ с центром в S, расположив оси X и Y в плоскости сечения, а ось Z -перпендикулярно ему, и спроектировать на указанные оси векторы 
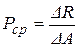 .
.
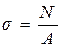 , (2.1)
, (2.1)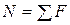 . (2.2)
. (2.2) .
. , (2.3)
, (2.3) . (2.4)
. (2.4) , (2.5)
, (2.5) - допускаемое нормальное напряжение для материала стержня;
- допускаемое нормальное напряжение для материала стержня;
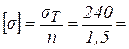 160 МПа.
160 МПа. мм2.
мм2. При этом
При этом  мм.
мм. мм2.
мм2. МПа< [ s ];
МПа< [ s ]; -153 МПа< [ s ];
-153 МПа< [ s ]; -102 МПа< [ s ].
-102 МПа< [ s ].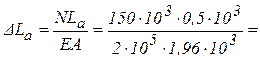 0,15 мм;
0,15 мм; мм;
мм; мм.
мм.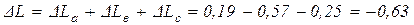 мм.
мм.


