
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напряжения в поперечных сечениях вала при крученииСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
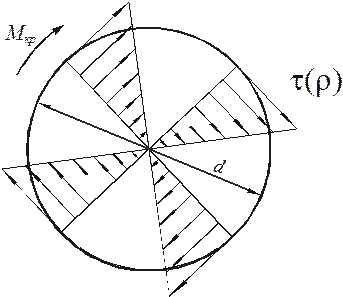
Поворот при кручении смежных поперечных сечений друг относительно друга вокруг оси вала вызывает появление в них касательных напряжений t. Сдвиги элементарных площадок смежных сечений происходят в направлениях, перпендикулярных радиусам. Так же направлены и напряжения t, которые вдоль радиусов изменяются по закону прямой линии (рис. 3.1). Внутренний крутящий момент Мкр в поперечном сечении рассматриваемой части вала, действующий со стороны его отброшенной части, является результирующим моментом всех напряжений t, действующих по сечению, относительно оси вала.
где Mкp - внутренний крутящий момент в рассматриваемом поперечном сечении; Jp - полярный момент инерции рассматриваемого сечения. Из формулы (3.8) следует, что максимальные касательные напряжения в конкретном поперечном сечении возникают в точках, наиболее удаленных от оси вала, то есть у его поверхности (при ρ=ρmax=0,5d).
где Для сплошного вала
Рисунок 3.1 - Схема распределения касательных напряжений по поперечному сечению вала Подбор сечений валов
Для обеспечения надежной работы валы должны удовлетворять условию прочности и условию жесткости. Для валов, работающих на чистое кручение, условие прочности имеет вид
где [ t ] - допускаемое касательное напряжение для материала вала. Отсюда полярный момент сопротивления сечения, удовлетворяющий условию прочности:
Валы на чистое кручение никогда не работают, так как всегда кроме кручения испытывают изгиб от собственной силы тяжести, сил тяжести насаженных на него элементов передач и усилий в этих передачах. Однако даже при значительных изгибных нагрузках, при приближенных прикидочных расчетах валы считают работающими на чистое кручение, а действие изгиба косвенно учитывают путем понижения допускаемого напряжения [ t ]. Условие жесткости при кручении для валов имеет вид
где [ q ] - допустимое значение относительного угла закручивания. Отсюда полярный момент инерции сечения, удовлетворяющий условию жесткости,
При подборе сечений валов используют оба условия: условие прочности (3.10) и условие жесткости (3.11). При этом диаметр вала принимается равным большему из двух полученных значений, округленному в большую сторону до ближайшего стандартного. Пример расчета
На передаточный вал сплошного круглого постоянного поперечного сечения (рис. 3.2,a) насажены четыре шкива. Шкив С получает от двигателя внешний крутящий момент mС. Шкивы А, В, Д входят в ременные передачи, вторые шкивы которых насажены на три вала, параллельные рассматриваемому, со стороны которых он через эти шкивы получает внешние моменты mA, mB, mД. Три из четырех указанных моментов известны по величине и направлению, четвертый – неизвестен ни по величине, ни по направлению. mС=2100 Нм; mA=600 Нм; mД=800 Нм; G=8×104 МПа; [ τ ] =20 МПа; [ θ ] =0,25 Для заданного вала построить эпюру внутренних крутящих моментов и определить диаметр, обеспечивающий его прочность и жесткость.

Рисунок 3.2 – Расчетная схема вала и эпюра внутренних крутящих моментов Мкр.z 1) Определим внешний момент mB, для чего используем уравнение равновесия вала (3.2). Будем смотреть на вал слева, считая положительным направление m против часовой стрелки. Искомый момент mB предварительно направим против часовой стрелки. Моментами трения в опорах вала будем пренебрегать. ΣmZ = mА + mВ - mС + mД = 0; mВ = -mА + mС - mД = - 600 + 2100 - 800 = 700 Нм. Знак искомого момента mВ получился положительным, следовательно, его направление было выбрано верно. 2) Определим внутренние крутящие моменты в поперечных сечениях участков вала, используя указанное выше правило знаков (см. стр. 14). При этом будем перемещаться вдоль вала слева направо, отбрасывая левые и рассматривая правые его части. При 0 £ Z £ 0,2 м: Мкр.z=mА=600 Нм. При 0,2 м £ Z £ 0,5 м: Мкр.z=mА+mВ=600+700=1300 Нм. При 0,5 м £ Z £ 0,9 м: Мкр.z=mА+mВ-mС=600+700–2100=-800 Нм. Проверим последнее значение Мкр.z ходом справа налево: При 0 £ Z £ 0,4 м: Мкр.z=-mД=-800 Нм. Эпюра Мкр.z показана на рис. 3.2,б. 3) Определим диаметр вала, обеспечивающий условие его прочности:
Для сплошного вала Wp= Отсюда С целью приведения в соответствие размерностей числителя и знаменателя выражения для d значение момента Мкр.max подставляем в него в Н×мм. 4) Определим диаметр вала, обеспечивающий условие жесткости
Для сплошного вала Jp= Отсюда где Окончательно принимаем d=80 мм. 5) Проверим прочность и жесткость рассматриваемого вала при d=80 мм.
где
где
Вопросы для самоконтроля 1 Какой вид нагружения называют кручением? 2 В каких случаях вал будет работать начистоекручение? 3 Как по передаваемой мощности определить соответствующий крутящий момент? 4 Какую величину называют полярным моментом инерции сечения? Какова его единица измерения? 5 Какую величину называют полярным моментом сопротивления сечения? Какова его единица измерения? 6Что такое относительный угол закручивания? 7 Как распределяются касательные напряжения по поперечному сечению вала при кручении? 8 В каких точках вала возникают наибольшие касательные напряжения при кручении? 9 Как выглядит условие прочности вала при кручении? 10 Как выглядит условие жесткости вала при кручении? 11 Какие напряжения возникают в поперечных, продольных и наклонных сечениях вала при кручении? 12 В чем заключается закон парности касательных напряжений?
|
||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 4431; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.110.182 (0.01 с.) |

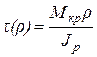 , (3.8)
, (3.8) (3.9)
(3.9) - полярный момент сопротивления сечения кручению.
- полярный момент сопротивления сечения кручению.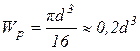 .
.
 , ( 3. 10 )
, ( 3. 10 ) .
.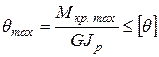 , (3.11)
, (3.11)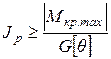 .
. .
. .
. .
.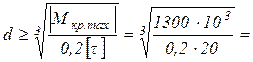 69 мм.
69 мм. .
. .
. 78 мм,
78 мм,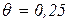
 =
= 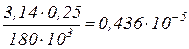
 .
. 12,7 МПа< [ t ],
12,7 МПа< [ t ], мм3.
мм3.
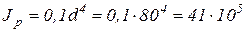 мм4.
мм4.


