
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напряжения в поперечном сеченииСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Опыты показывают, что если на поверхности бруса круглого сечения нанести прямоугольную сетку, а на торцевой поверхности нанести радиальные линии (рис.5.5), то после деформации кручение окажется что: - все образующие поворачиваются на один и тот же угол - торцевые сечения остаются круглыми, плоскими, расстояния между ними не меняются; - каждое сечение поворачивается относительно другого на некоторый угол - радиальные линии на торцевой поверхности остаются прямыми. На основании этих наблюдений можно заключить, что может быть принята гипотеза Бернулли (гипотеза плоских сечений), а в вале возникают условия чистого сдвига, в поперечных сечениях действуют только касательные напряжения, нормальные напряжения равны нулю. Рассмотрим поперечное сечение вала, расположенное на некотором расстоянии z от торцевого, где Мк=T (рис.5.5). На элементарной площадке dF будет действовать элементарная сила
26 вопрос- Расчеты на прочность при кручении Условие прочности бруса при кручении заключается в том, что наибольшее касательное напряжение, возникающее в нем, не должно превышать предельно допустимое. При этом расчетная формула на прочность имеет вид: τmax = Мкр / Wr ≤ [τкр], где [τкр] - предельное допускаемое напряжение. При практических расчетах, определяя предельные допускаемые напряжения для различных материалов, используют зависимость между напряжениями при растяжении и напряжениями при кручении, которая для стали и чугуна имеет вид: для стали - [τкр] = 0,55....0,6 [σр] (здесь [σр] - справочная или определяемая экспериментально величина, (предельное допустимое напряжение растяжения) характеризующая материал бруса (вала).
27 вопрос- Расчет на жесткость при кручении Кроме требования прочности к валам предъявляются требования жесткости, которое заключается в том, что угол закручивания участка вала длиной 1 м не должен превышать предельной величины, определяемой требованиями конструкции. Допускаемый угол закручивания 1 м длины вала задается в градусах и обозначается [φ0°]. φ0°= 180 Мкр / (пGIr) ≤ [φ0°] В реальных механизмах обычно допускаются углы закручивания валов в пределах [φ0°] = 0,25...1 градус/м. 28 вопрос- Изгиб, основные определения Изгиб — в сопротивлении материалов вид деформации, при котором происходит искривление осей прямых брусьев или изменение кривизны осей кривых брусьев. Изгиб связан с возникновением в поперечных сечениях бруса изгибающих моментов. Прямой изгиб возникает в случае, когда изгибающий момент в данном поперечном сечении бруса действует в плоскости, проходящей через одну из главных центральных осей инерции этого сечения. В случае, когда плоскость действия изгибающего момента в данном поперечном сечении бруса не проходит ни через одну из главных осей инерции этого сечения, изгиб называется косым. Если при прямом или косом изгибе в поперечном сечении бруса действует только изгибающий момент, то соответственно имеется чистый прямой или чистый косой изгиб. Если в поперечном сечении действует также и поперечная сила, то имеется поперечный прямой или поперечный косой изгиб. Часто термин «прямой» в названии прямого чистого и прямого поперечного изгиба не употребляют и их называют соответственно чистым изгибом и поперечным изгибом.
29 вопрос- Внутренние силовые факторы при изгибе.Изгибающий момент Изгибающий момент — момент внешних сил относительно сечения балки. Для внутренних усилий приняты следующие правила знаков.
График, показывающий изменение изгибающего момента вдоль оси балки, называется эпюрой изгибающих моментов (Эп. Мх). График, показывающий изменение поперечной силы вдоль оси балки, называется эпюрой поперечных сил (Эп. Qy). Для построения эпюр находят опорные реакции балки, потом балку разделяют на участки, на каждом из которых получают методом сечений уравнения Внутренние усилия возникают во всех точках поперечного сечения балки и распределены по неизвестному закону. Не имея возможности определить эти внутренние усилия для каждой точки сечения, заменяем их статически эквивалентными внутренними силовыми факторами, приложенными в центре тяжести поперечного сечения. Внутренние силовые факторы определяются из условия равновесия рассматриваемой части балки. Однако можем внутренние силовые факторы найти и непосредственно, как действие отброшенной левой части на правую часть. При прямом изгибе в поперечном сечении балки возникают два внутренних силовых фактора: изгибающий момент, численно равный алгебраической сумме моментов всех сил, приложенных к отбрасываемой части балки, относительно главной центральной оси, проходящей через центр тяжести рассматриваемого сечения (в рассмотренном нами случае изгибающий момент равен: поперечная сила, численно равная алгебраической сумме всех внешних сил (активных и реактивных), действующих на отбрасываемую часть балки (в нашем случае поперечная сила равна:
|
||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1314; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.105.85 (0.009 с.) |

 , а прямоугольники, нанесенные на поверхности, превращаются в параллелограммы;
, а прямоугольники, нанесенные на поверхности, превращаются в параллелограммы;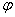 , называемый углом закручивания;
, называемый углом закручивания; , момент который относительно оси вала равен
, момент который относительно оси вала равен  . Крутящий момент М к, в сечении равен
. Крутящий момент М к, в сечении равен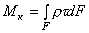 .
.
 , поперечной силой
, поперечной силой  и интенсивностью распределенной нагрузки
и интенсивностью распределенной нагрузки  существуют дифференциальные зависимости
существуют дифференциальные зависимости
 ;
;  ;
; 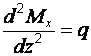 .
.
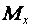 и
и  );
); ).
).


