
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эквивалентное (приведенное) напряжениеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Equivalent stress Напряжение одноосного растяжения (сжатия), равноопасного рассматриваемому сложному напряженному состоянию. Вопрос Растяжение (сжатие) - это вид деформации стержня, при котором происходит изменение его первоначальной длины. Растяжение (сжатие) вызывается внешними силами, действующими вдоль оси стержня z. При этом в любом поперечном сечении стержня возникает только одно внутреннее усилие – продольная сила (N), которая является равнодействующей всех внутренних сил, возникающих в каждой точке этого сечения и направленных параллельно оси стержня. Вопрос Если продольные силы, возникающие в различных поперечных сечениях стержня, неодинаковы, закон их изменения по длине стержня представляется в виде графика N(z), называемого эпюрой продольных сил. Эпюра продольных сил необходима для оценки прочности стержня и строится для того, чтобы найти опасное сечение (поперечное сечение, в котором продольная сила принимает наибольшее значение КАК СТРОИТЬ ЭПЮРУ ПРОДОЛЬНЫХ СИЛ? Для построении эпюры N используется метод сечений. Продемонстрируем его применение на примере (рис. 2.1).
Разрежем стержень в этом месте и мысленно отбросим нижнюю его часть (рис. 2.1, а). Далее мы должны заменить действие отброшенной части на верхнюю часть стержня внутренней продольной силой N. Для удобства вычисления ее значения закроем рассматриваемую нами верхнюю часть стержня листком бумаги. Напомним, что продольное усилие N, возникающее в поперечном сечении, можно определить как алгебраическую сумму всех продольных сил, действующих на отброшенную часть стержня, то есть на ту часть стержня, которую мы видим. При этом применяем следующее правило знаков: силы, вызывающие растяжение оставленной части стержня (закрытой нами листком бумаги) входят в упомянутую алгебраическую сумму со знаком «плюс», а силы, вызывающие сжатие – со знаком «минус». Итак, для определения продольной силы N в намеченном нами поперечном сечении необходимо просто сложить все внешние силы, которые мы видим. Так как сила Знак «минус» означает, что в этом сечении стержень испытывает сжатие. Можно найти опорную реакцию R (рис. 2.1, б) и составить уравнение равновесия для всего стержня, чтобы проверить результат:
или
Теперь заменим действие отброшенной нижней части неизвестным внутренним усилием N, направив его, например, от сечения, что соответствует растяжению. Уравновешиваем оставленную нами верхнюю часть стержня:
Знак «минус» сигнализирует, что мы не угадали направление продольного усилия N. Оно будет не растягивающим, как мы предполагали, а сжимающим. Таким образом, мы получили тот же самый результат. Вопрос Пусть в результате деформации первоначальная длина стержня l станет равной. l 1. Изменение длины
называется абсолютным удлинением стержня. Отношение абсолютного удлинения стержня к его первоначальной длине называется относительным удлинением (
При растяжении продольная деформация считается положительной, а при сжатии – отрицательной. Поперечные размеры стержня в результате деформирования также изменяются, при этом при растяжении они уменьшаются, а при сжатии – увеличиваются. Если материал является изотропным, то его поперечные деформации равны между собой:
Опытным путем установлено, что при растяжении (сжатии) в пределах упругих деформаций отношение поперечной деформации к продольной является постоянной для данного материала величиной. Модуль отношения поперечной деформации к продольной, называемый коэффициентом Пуассона иликоэффициентом поперечной деформации, вычисляется по формуле:
Для различных материалов коэффициентПуассона изменяется в пределах
Вопрос Для большинства конструкционных материалов между напряжением (
Закон Гука: Напряжение пропорционально деформации. Впервые Закон Гука был опубликован в виде анаграммы английским ученым Робертом Гуком (1635 – 1703 гг.). При правильной расстановке букв анаграмма читается: «Каково удлинение, такова и сила». К такому же заключению в 1680 г., независимо от Гука, пришел французский ученыйЭдмон Мариотт. Коэффициент пропорциональности (E) в формуле закона Гука Необходимо отметить, что некоторые материалы не подчиняются законуГука, например, кожа, ткани. Такие материалы, как, например, чугун, только с некоторым приближением можно считать подчиняющимся закону Гука. Но даже и те материалы, которые подчиняются закону Гука, перестают ему следовать при достижении деформации определенного значения. Из закона Гука видно: чем больше модульЮнга, тем меньше (при том же значении напряжения) деформация материала. Следовательно, модуль продольной упругости характеризует жесткость материала при растяжении (сжатии). Из формулы закона Юнга видно, что модульЮнга измеряется в тех же единицах, что и нормальное напряжение ( Так, например, для всех марок сталей
Вопрос Для большинства конструкционных материалов между напряжением (
Закон Гука: Напряжение пропорционально деформации. Впервые Закон Гука был опубликован в виде анаграммы английским ученым Робертом Гуком (1635 – 1703 гг.). При правильной расстановке букв анаграмма читается: «Каково удлинение, такова и сила». К такому же заключению в 1680 г., независимо от Гука, пришел французский ученыйЭдмон Мариотт. Коэффициент пропорциональности (E) в формуле закона Гука Необходимо отметить, что некоторые материалы не подчиняются законуГука, например, кожа, ткани. Такие материалы, как, например, чугун, только с некоторым приближением можно считать подчиняющимся закону Гука. Но даже и те материалы, которые подчиняются закону Гука, перестают ему следовать при достижении деформации определенного значения. Из закона Гука видно: чем больше модульЮнга, тем меньше (при том же значении напряжения) деформация материала. Следовательно, модуль продольной упругости характеризует жесткость материала при растяжении (сжатии). Из формулы закона Юнга видно, что модульЮнга измеряется в тех же единицах, что и нормальное напряжение ( Так, например, для всех марок сталей Вопрос Механические характеристики материала определяются в результате испытания образца на специальных прессах. Форма образца может быть различной, но чаще всего стержень с участком постоянного поперечного сечения (круглого или прямоугольного) длиной
Современные испытательные машины снабжены записывающим прибором, который при испытании образца автоматически вычерчивает график зависимости между нагрузкой (P) и абсолютным удлинением ( Рассмотрим диаграмму растяжения для стали марки Ст. 3 (рис. 2.3). Эта диаграмма характеризует поведение данного образца, но не материала, из которого он сделан. В начальной стадии испытания, до точки А с ординатой При некотором значении растягивающей силы За точкой C диаграммы удлинение образца начинает расти быстрее нагрузки. Число линий Людерса – Чернова растет, они сливаются друг с другом и, наконец, теряют ясность своих очертаний. Этот участок диаграммы растяжения называется зоной упрочнения. В наивысшей точке диаграммы D при силе равной Сопротивление образца растяжению, после образования шейки, падает и его разрыв происходит в точке K при нагрузке:
При разрыве образца, как правило, появляется поперечная трещина в центре тяжести поперечного сечения (посредине шейки), а остальная часть сечения скалывается под углом Линия разгрузки образца KL оказывается прямой и параллельной начальному участку диаграммы ОА. Следовательно, полная деформация образца состоит из двух частей: упругой, исчезающей после снятия нагрузки, и остаточной (пластической).
Строительные материалы (бетон, цемент) в основном испытывают на сжатие. Дерево испытывают на сжатие как вдоль, так и поперек волокон. Сталь испытывают на сжатие значительно реже, чем на растяжение. Образцы для испытания на сжатие имеют, как правило, форму кругового цилиндра с отношением высоты образца к диаметру не более 3. Для стали Ст. 3 диаграмма сжатия вплоть до предела текучести почти полностью повторяетдиаграмму растяжения , то есть . . Различие начинает сказываться после наступления текучести. Площадка текучести при сжатии менее четко выражена, чем при растяжении. При больших деформациях различие становится особенно ощутимым, и в первую очередь из-за того, что сжатие сопровождается увеличением площади поперечного сечения образца, вследствие чего испытание требует постоянно возрастающей нагрузки.
Следовательно, при сжатии пластичного материала получить такую характеристику, как предел прочности, не представляется возможным. Исследуемый образец, не претерпевая разрушения, расплющивается, и дальнейшее испытание на сжатие ограничивается возможностями пресса. В расчетной практике предел прочности пластичного материала на сжатие условно принимается таким же, как и на растяжение. Диаграмма сжатия хрупкого материала по виду напоминает диаграмму растяжения, но предел прочности на сжатие, как правило, в несколько раз больше, чем на растяжение ( Наглядное представление о сравнительных механических характеристиках низкоуглеродистой стали и серого чугуна при растяжении и сжатии дают диаграммы, показанные на рис. 2.5. Вопрос Применяемые в инженерной практике материалы можно разделить на 2 группы: пластичные, которые разрушаются после появления значительных остаточных деформаций и хрупкие, которые разрушаются при весьма малых деформациях.
Это деление является условным, ибо один и тот же материал в зависимости от характера напряженного состояния, температуры и скорости деформирования может вести себя, как пластичный или как хрупкий. Поэтому при решении задач по сопромату правильнее говорить о пластичном или хрупком состоянии материала.
Основные механические характеристики пластичного материала (например, малоуглеродистой стали) определяются при испытании на растяжение. На рис. 6,а показана типичная диаграмма растяжения образца из малоуглеродистой стали. Диаграмма характеризует поведение данного индивидуального образца с его конкретными размерами. Для того тобы получить механические характеристики исследуемого материала, необходимо исключить влияние абсолютных размеров образца. С этой целью диаграмму перестраивают в координатах
где Ао и l - соответственно начальная площадь поперечного сечения и начальная расчетная длина образца (рис. 6 б).
Характер диаграммы после такой.перестройки сохраняется, изменяется лишь масштаб. Эта диаграмма называется диаграммой растяжения материала или диаграммой напряжений, и ее. ординаты дают величины механических характеристик исследуемого материала. В начальной стадии испытания (до точки А с координатой Fпц) зависимость между силой и удлинением линейна, т.е. справедлив закон Гука. Участок диаграммы ОА называется зоной пропорциональности. При растягивающей силе Fу, почти не отличающейся от Fпц, в образце возникают первые остаточные деформации. Участок 0В - зона упругости. При достижении растягивающей силой значения Fт (точка С) наблюдается рост удлинения без увеличения нагрузки. Это явление называется текучестью металла. Соответствующий участок диаграммы (почти горизонтальная линия) называется площадкой текучести. В этой стадии деформации полированная поверхность образца становится матовой и на ней можно обнаружить сетку линий, наклоненных к оси образца под углом примерно 45°. Это линии Людерса-Чернова, представляющие собой следы сдвигов частиц материала. Направление указанных линий соответствует площадкам, на которых при растяжении образца возникают наибольшие касательные напряжения.
По окончании стадии текучести материал вновь начинает сопротивляться деформации, здесь связь между силой и удлинением не линейна: удлинение растет быстрее нагрузки. Этот участок диаграммы (СД) называют зоной упрочнения. При силе примерно равной Fmax на образце появляется местное утоньшение - шейка, в результате сопротивление образца падает и его разрыв происходит при силе, меньшей Fпч. Участок диаграммы ДЕ - зона локализации деформаций. При решении задач по сопромату наиболее важням является участок, при котором деформация прямопропрциональна нагрузке.
Вопрос Понятие диаграммы растяжения встречается в лекции Испытание материала на растяжение. Диаграмма растяжения для разных материалов имеет неодинаковый вид. На рис. 2.4 из лекции по ссылке выше приведена диаграмма растяжения для стали Ст. 3. Этот материал относится к пластичным материалам, которые имеют площадку текучести, и разрушаются при больших остаточных деформациях. Необходимо, правда, отметить, что не для всех пластичных материалов площадка текучести имеет четко выраженный характер. Для таких материалов вводится понятие условного (или технического) предела текучести, представляющего собой напряжение, которое возникает в материале образца при относительном удлинении, равном 0,2 %. Иногда условный предел текучести обозначают Заметим, что пластичность – это положительное свойство материала. Она играет большую роль в обеспечении безопасности и надежности конструкций. Пластические свойства материала оцениваются следующими двумя характеристиками, которые также определяют при испытании на растяжение: относительным остаточным удлинением образца при разрыве (%):
где относительным поперечным сужением образца при разрыве(в %):
где Но существуют материалы, например чугун, которые характерны тем, что они вообще не имеют площадки текучести, и их разрушение происходит без образования шейки (диаграмма растяжениядля них обрывается сразу же после достижения предела прочности) и при очень малых остаточных деформациях (хрупкие материалы). Вопрос Срез - это непосредственное разрушение материала стержня, происходящее в результате деформации сдвига. Под сдвигом понимается, угловая деформация или вид напряженного состояния – чистый сдвиг. При проверке прочности соединений предпочтительнее говорить: «расчет на срез». Если речь о напряженном состоянии, то правильнее говорить: «напряженное состояние при сдвиге». Вопрос Установлено: касательные напряжения пропорциональны углу сдвига в определенных пределах упругой деформации сдвига. Соотношение Коэффициент пропорциональности G в формуле закона Гука при сдвиге - модуль сдвига. Модуль сдвига измеряется в МПа, кН/см2, кгс/см2, кгс/мм2. Угол сдвига Модуль сдвига (G) – это физическая постоянная для материала, характеризующая жесткость при сдвиге. Значение модуля сдвига (G) может быть определено экспериментально. Вопрос Смятие- -вид местной пластической деформации, возникающий при сжатии твердых тел, в местах их контакта.
Вопрос
Вопрос Осевым моментом инерции сечения (second moment of area или second moment of inertia) относительно оси x называется сумма произведений элементарных площадок dA на квадрат их расстояний до данной оси, численно равная интегралу Jx= И относительно оси y: Jy=
Полярным моментом инерции сечения относительно данной точки J
Центробежным моментом инерции сечения относительно осей x и y называется сумма произведений элементарных площадок dA на их расстояния до этих осей: Jxy=
Центробежный момент инерции может быть положительным, отрицательным и, в частном случае, равным нулю. Если взаимно перпендикулярные оси x и y или одна из них являются осями симметрии фигуры, то относительно таких осей центробежный момент инерции равен нулю. Jxy =0.
Вопрос 1.3. Моменты инерции простых сечений.
1. Прямоугольник (рис. 1.5,а). Вычислим момент инерции сечения относительно оси Х0, проходящей через центр тяжести параллельно основанию. За dA примем площадь бесконечно тонкого слоя dA = bdy. Тогда Аналогично, получим 2. Круг (рис. 1.5,б). Сначала определим полярный момент инерции относительно центра круга За dA принимаем площадь бесконечно тонкого кольца толщиной dp тогда Следовательно, Теперь легко найдем Ixo. Действительно, для круга согласно формуле (1.9.), имеем Iр = 2Iхо = 2Iуо, откуда 2. Кольцо (рис. 1.5,в). Осевой момент инерции в этом случае равен разности моментов инерции внешнего и внутреннего кругов Аналогично полярный момент инерции 2. Треугольник (рис. 1.5,г). Определим момент инерции относительно оси x1, параллельной основанию и проходящей через вершину треугольника За dA примем площадь бесконечно тонкой трапеции KBDE, площадь которой можно считать равной площади прямоугольника: dA = bydy, где by - длина прямоугольника. Легко получить из подобия треугольников by = yb/h; тогда Определим момент инерции относительно центральной оси; для этого используем формулу (1.10) Определим момент инерции относительно оси, проходящей через основание: Вопрос Кручение появится, если неподвижно закрепить, например, левый конец стержня круглого поперечного сечения и приложить к правому концу скручивающий момент ( Угол закручивания ( Вопрос Стержни (брусья), пластины (оболочки), массивные тела. Внешние силы, действующие на тело, вызывают в нем дополнительные внутренние силы, стремящиеся противодействовать деформации. Обнаружить возникающие в нагруженном теле вн. силы можно, применив метод сечений.- внеш силы, приложенные к отсеченной части тела, уравновешиваются внутр силами, возникающими в плоскости сеч-я и заменяющими действие отброшенной части тела на остальную. В сеч-и возникают внутренние силы, уравновешивающие внешние силы, приложенные к оставленной части. Это позволяет применить, к любой части тела условия равновесия ΣFix=0, ΣFiy=0, ΣFix=0, ΣFiz=0, ΣMix=0,.. Для расчета элементов конструкций на прочность, жесткость и устойчивость прежде всего необходимо с помощью м-да сеч-й определить возникающие внутренние силовые факторы. При действии пространственной сис-мы сил из уравнения равновесия можно найти возникающие в поперечном сеч-ии три составляющие силы N, Qx и Qy (составляющие главного вектора внутренних сил), направленные по координатным осям, и три составляющие момента Мх, Му, Мz (составляющие главного момента внутренних сил). Указанные силы и моменты, являющиеся внутренними силовыми факторами (рис. 56, в), соответственно называются: N — продольная сила; Qx и Qy — поперечные силы; Мх и My — изгибающие моменты; Мz — крутящий момент. Для определения внутренних силовых факторов: Мысленно провести сеч-е в интересующей нас т-ке и рассм-ть равновесие оставленной части, составить уравнения равновесия для оставленной части и определить из них значения и направления внутренних силовых факторов. При осевом растяж-и и сжатии вн силы упругости м.б заменены одной продольной силой N. Сдвиг — когда в попереч сечении вн силы упругости приводятся к одной силе в плоскости сечения. При кручении только крутящий момент, если есть изгиб-щий момент — деформация чистого изгиба. 24 вопрос-Эпюра крутящих моментов Кручение стержня вызывается парами сил (сосредоточенными или распределенными), плоскость действия которых перпендикулярна продольной оси стержня. При кручении в поперечном сечении стержня возникает лишь один силовой фактор – крутящий момент Mк. Согласно методу сечений величина и направление крутящего может быть найдены из уравнения равновесия моментов относительно оси стержня, составленного для оставленной части. То есть, крутящий момент в сечении численно равен алгебраической сумме моментов пар сил, приложенных по одну сторону от рассматриваемого сечения, относительно продольной оси стержня. Правило знаков для крутящих моментов.
Крутящий момент для сечения можно выразить так: Mк(x)=
Распределенный крутящий момент m может быть постоянной или переменной интенсивности. Для постоянного распределенного момента m это выражение примет вид: Mк(x)= где Lmн и Lmк – расстояние от начала координат до начала и до конца распределенного момента соответственно. Дифференциальная зависимость внутренних усилий от распределенной нагрузки m: dMк = m·dx
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1153; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.176.112 (0.011 с.) |

 ).
). Определим продольную силу N, возникающую в намеченном нами поперечном сечении стержня.
Определим продольную силу N, возникающую в намеченном нами поперечном сечении стержня. кН растягивает верхнюю часть, а сила
кН растягивает верхнюю часть, а сила  кН ее сжимает, то
кН ее сжимает, то  кН.
кН.
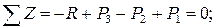
 кН.
кН.
 кН.
кН.
 – эпсилон) или продольной деформацией. Продольная деформация – это безразмерная величина. Формула безразмерной деформации:
– эпсилон) или продольной деформацией. Продольная деформация – это безразмерная величина. Формула безразмерной деформации: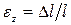
 .
.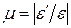
 . Например, для пробки
. Например, для пробки  , для каучука
, для каучука 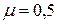 , для стали
, для стали  , для золота
, для золота  .
. ) и продольной деформацией(
) и продольной деформацией(
 МПа.
МПа.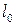 . Концы образца имеют специальные утолщения для их закрепления в испытательной машине.
. Концы образца имеют специальные утолщения для их закрепления в испытательной машине. Перед началом испытания материала на растяжение замеряется площадь поперечного сечения (
Перед началом испытания материала на растяжение замеряется площадь поперечного сечения ( ) средней части образца. Значение растягивающей силы (P) и удлинения его средней части (
) средней части образца. Значение растягивающей силы (P) и удлинения его средней части ( ) в каждый момент нагружения определяются специальными устройствами. При испытании нагрузка увеличивается медленно и плавно.
) в каждый момент нагружения определяются специальными устройствами. При испытании нагрузка увеличивается медленно и плавно. , зависимость между силой (P) и удлинением (
, зависимость между силой (P) и удлинением (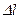 ) носит линейный характер, что свидетельствует о линейной деформируемости образца. Затем диаграмма искривляется и при некотором значении растягивающей силы
) носит линейный характер, что свидетельствует о линейной деформируемости образца. Затем диаграмма искривляется и при некотором значении растягивающей силы  наблюдается значительный рост удлинения образца без увеличения нагрузки (текучесть материала). Практически горизонтальный участок диаграммы BC называется площадкой текучести, а точка B – критической точкой диаграммы.
наблюдается значительный рост удлинения образца без увеличения нагрузки (текучесть материала). Практически горизонтальный участок диаграммы BC называется площадкой текучести, а точка B – критической точкой диаграммы. к оси образца. Далее появляется вторая система линий, пересекающая первую и наклоненную к оси под тем же углом, что и первая. Такая система сопряженных линий называется линиями Людерса – Чернова, представляющие собой следы сдвигов частиц материала. Направления линий Людерса-Чернова соответствует площадкам, на которых при растяжении возникают наибольшие касательные напряжения.
к оси образца. Далее появляется вторая система линий, пересекающая первую и наклоненную к оси под тем же углом, что и первая. Такая система сопряженных линий называется линиями Людерса – Чернова, представляющие собой следы сдвигов частиц материала. Направления линий Людерса-Чернова соответствует площадкам, на которых при растяжении возникают наибольшие касательные напряжения. на образце внезапно появляется местное сужение – шейка, которая представляет собой результат накопления деформаций сдвига.
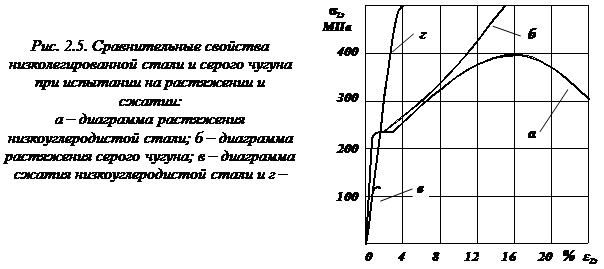
на образце внезапно появляется местное сужение – шейка, которая представляет собой результат накопления деформаций сдвига. .
.
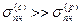 ). Разрушение образца при сжатии происходит обычно путем сдвига одной части относительно другой, происходящим примерно под углом
). Разрушение образца при сжатии происходит обычно путем сдвига одной части относительно другой, происходящим примерно под углом 

 .
. ,
, – конечная длина расчетной части образца;
– конечная длина расчетной части образца; ,
, – площадь поперечного сечения образца в месте разрыва.
– площадь поперечного сечения образца в месте разрыва. - формула закона Гука при сдвиге.
- формула закона Гука при сдвиге. –безразмерная величина.
–безразмерная величина.




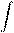 Ay2dA
Ay2dA =
= 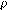 2dA
2dA

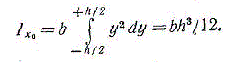
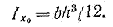 (1.11)
(1.11) (1.12)
(1.12)


 (1.13)
(1.13) (1.14)
(1.14) (1.15)
(1.15) (1.16)
(1.16)
 (1.17)
(1.17) (1.18)
(1.18)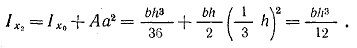 (1.19)
(1.19)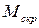 ) относительно оси стержня z. В стержне появится деформация кручения: одно поперечное сечение повернется на некоторый угол относительно другого (расстояние между сечениями останется прежним, если угол поворота мал). В поперечных сечениях стержня, при кручении, возникнет только одно внутреннее усилие – крутящий момент (
) относительно оси стержня z. В стержне появится деформация кручения: одно поперечное сечение повернется на некоторый угол относительно другого (расстояние между сечениями останется прежним, если угол поворота мал). В поперечных сечениях стержня, при кручении, возникнет только одно внутреннее усилие – крутящий момент ( ).
). )- угол, на который повернется крайнее правое поперечное сечение стержня относительно неподвижного левого сечения.
)- угол, на который повернется крайнее правое поперечное сечение стержня относительно неподвижного левого сечения. Крутящий момент считается положительным, если при взгляде на сечение со стороны внешней нормали он поворачивает сечение по ходу часовой стрелки и отрицательным — в противном случае.
Крутящий момент считается положительным, если при взгляде на сечение со стороны внешней нормали он поворачивает сечение по ходу часовой стрелки и отрицательным — в противном случае. Это правило знаков условное и не совпадает с принятыми правилами знаков моментов, углов поворота в теоретической механике и математике, поскольку связано не с системой координат, а с видом деформации оставленной части.
Это правило знаков условное и не совпадает с принятыми правилами знаков моментов, углов поворота в теоретической механике и математике, поскольку связано не с системой координат, а с видом деформации оставленной части. Mкi+
Mкi+  dx
dx



