
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение напряжений в тонкостенных цилиндрическихСодержание книги
Поиск на нашем сайте
ВВЕДЕНИЕ В современных условиях химическое машиностроение является одной из наиболее бурно развивающихся отраслей машиностроения. Конструкции химических аппаратов становятся все более сложными, и на первый план выходит задача их расчета на прочность. Грамотно проведенный прочностной расчет позволяет снизить материалоемкость выпускаемой продукции, а следовательно, и ее стоимость. К схеме осесимметричной цилиндрической оболочки сводится очень много инженерных конструкций. Геометрическая форма объектов, которые могут быть причислены к оболочкам или пластинам, чрезвычайно разнообразна: в машиностроении - это корпуса всевозможных машин; в гражданском и промышленном строительстве - покрытия и перекрытия, навесы, карнизы; в кораблестроении - корпуса судов, сухих и плавучих доков; в авиастроении - фюзеляжи и крылья самолетов; в подвижном составе железнодорожного транспорта, кузова вагонов, цистерны, несущие конструкции локомотивов; в атомной энергетике - защитная конструкция атомных станций, корпуса реакторов и т.д. Неотъемлемой частью конструкций современной техники являются трубопроводы, которые нашли широкое применение в нефтяной и газовой промышленности, в химическом машиностроении, коммунальном хозяйстве. С одной стороны, это элементы транспортировки продукта и питания машин, технологических установок, с другой - элементы гидроавтоматики и управления. Расчет труб на прочность в решающей степени определяют работоспособность трубопроводных магистралей и конструкции в целом. Таким образом, в связи с интенсивным развитием химической промышленности в целом и нефтехимической в частности проблемы комплексного расчетного анализа элементов химических аппаратов и узлов приобретают особую актуальность. ЛАБОРАТОРНАЯ РАБОТА № 1 Определение напряжений в тонкостенных цилиндрических Оболочках, работающих под действием внутреннего давления Корпуса химических аппаратов состоят из обечаек и днищ и, как правило, изготавливаются из одного и того же материала. Под действием внутреннего давления стенки аппарата находятся в объемном напряженном состоянии, когда вдоль образующей действует меридиональное (осевое) напряжение ss, по касательной окружности – кольцевое напряжение st и по нормам к стенке – радиальное напряжение sr . Все три напряжения являются нормальными и главными, так как они действуют в сечении, в котором отсутствуют касательные напряжения.
Особенностью расчета тонкостенных аппаратов, у которых толщина стенки много меньше диаметра, является то, что можно пренебречь радиальными напряжениями sr, величина которых невелика и по абсолютному значению не превышает давление среды в аппарате, т.е. sr @ 0. Исходя из другого допущения, что напряжения ss, и st равномерно распределяются по толщине стенки, можно предположить, что отсутствует изгиб оболочки, и основанная на этом предположении теория расчета называется безмоментной или мембранной. ЦЕЛЬ РАБОТЫ Исследовать напряженное состояние тонкостенных оболочек различной формы, находящихся под действием внутреннего давления. СОДЕРЖАНИЕ РАБОТЫ Оболочкой называется тело, ограниченное двумя криволинейными поверхностями, расстояние между которыми мало по сравнению с другими размерами. Геометрическое место точек, равноотстоящих от обеих поверхностей оболочки, носит название срединной поверхности. При расчете тонкостенных оболочек все нагрузки, действующие на них, прикладывают к срединной поверхности оболочки. Если срединная поверхность оболочки является плоскостью, то такую оболочку называют пластиной. Если срединная поверхность оболочки образует поверхность вращения в форме цилиндра, то оболочку называют цилиндрической. Меридианом называется линия пересечения срединной поверхности с плоскостью, проходящей через ось вращения оболочки (ОАВ). Параллелью называется линия пересечения срединной поверхности с поверхностью, перпендикулярной к меридиану (АА1А2). Кольцевым сечением называется сечение, перпендикулярное оси вращения оболочки и проходящее через ее параллель. Существует две теории определения напряжений в тонкостенных аппаратах: моментная и безмоментная (мембранная). В местах, удаленных на некоторое расстояние от линии сопряжения тонкостенных оболочек различной формы, расчет напряжений целесообразно производить по более простой безмоментной теории, расчетные формулы которой справедливы для срединной поверхности.
Основные положения безмоментной теории заключаются в следующем: 1) нагрузки, действующие на поверхности оболочки, могут считаться перпендикулярными им и симметричными относительно оси вращения оболочки; 2) вследствие малой толщины оболочки сопротивление изгибу отсутствует (изгибающий момент не возникает); 3) напряжения по толщине стенки оболочки распределены равномерно. Основными уравнениями безмоментной теории расчета являются уравнение Лапласа (уравнение 2.1) и уравнение равновесия зоны оболочки (уравнение 2.2), которые для аппаратов, нагруженных внутренним газовым давлением Р,соответственно запишутся соответственно:
где АС1=R1 – радиус кривизны меридиана или 1-й главный радиус, м; АС=R2 – радиус кривизны меридиана или 2-й главный радиус, м; АК=r – радиус кольцевого сечения оболочки, м;
Характерными геометрическими параметрами конических днищ является половина угла раскрытия конуса a и расстояние х от вершины конуса до исследуемой точки (рис. 2.2).
Учитывая, что для цилиндрической обечайки радиус кривизны меридиана R1 = ∞, а R2 = r = R (радиус срединной поверхности цилиндра), и угол широты φ = π/2, из уравнения (2.1) и (2.2) получим:
где S - меридиональная сила, т.е. сила, действующая на единицу длины параллельного круга, на всю толщину оболочки и лежащая в плоскости меридиана, Н/м (рис. 2.1); Т - кольцевая сила, т.е. сила действующая на единицу длины меридиана, на всю толщину оболочки и лежащая в плоскости параллели, Н/м. В случае газового давления величина давления постоянная во всех точках поверхности оболочки. Для резервуаров, наполненных жидкостью, давление по их высоте переменно. В этом случае необходимо учитывать, что если на какую-либо поверхность действует давление жидкости, то вертикальные составляющие сил давления равны весу жидкости в объеме, расположенном над поверхностью. Поэтому давление жидкости в различных сечениях оболочки будет различным в отличие от давления газа. Для конического днища имеем: R1 =∞, В этом случае: Для полушаровых днищ, у которых радиус является радиусом срединной поверхности шара (
На полюсе эллиптических днищ при
где а – большая полуось эллипса; в – малая полуось эллипса.
Рис. 2.3. Кольцевые и меридиональные напряжения, отнесенные к единице длины, в общем случае запишутся в виде выражений: st где δ - толщина оболочки, м. Тогда для любой формы тонкостенных оболочек, нагруженных внутренним давлением Р, имеем для цилиндрических обечаек: st ss Для конических днищ: st ss где xt и xs – расстояние от вершины конического днища до центра наклейки кольцевого и меридионального датчиков соответственно. Для шаровых днищ: st=ss На полюсе эллиптических днищ: st=ss= 3 ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ И МЕТОДИКАПРОВЕДЕНИЯ ЭКСПЕРИМЕНТА
Рис. 3.1 Основным элементом является горизонтальный цилиндрический аппарат. Рабочее давление в аппарате, заполненном касторовым маслом, создается грузопоршневым манометром 2 (МП-600). Под действием внутреннего давления в цилиндрической обечайке возникают деформации, которые воспринимаются тензодатчиками 3, наклеенными на наружной поверхности тонкостенной оболочки по кольцу и вдоль образующих. Сигнал от тензодатчиков через тарировочное устройство 4 («УТС-1») усиливается тензостанцией 5 («ТОПАЗ 3-4-01») и регистрируется электронно-цифровым вольтметром 6 («В7-20»). После снятия рабочего давления в аппарате с помощью индикатора часового типа 7, установленного на тарировочном устройстве 4, по показаниям электронно-цифрового вольтметра 6 определяется прогиб тарировочной балки 8, на которой наклеены компенсационные датчики 9, 10. С помощью электронно-цифрового вольтметра 6 снять показания с тензостанции 5 при ненагруженных тензодатчиках 3 и данные занести в таблицу 4.1. Закрыть вентиль 11 и нагрузить аппарат грузопоршневым манометром 2 до заданного значения внутреннего давления. Снять показания с тензостанции 5 с помощью электронно-цифрового вольтметра 6 и данные занести в таблицу 4.1. Открыть вентиль 11, сбросить давление в аппарате и выдержать 5 минут. Повторить испытание и, если показания не совпадают, подрегулировать каналы тензостанции 5. Создавая на тарировочной балке 8 нагрузку, величина которой должна соответствовать показаниям электронно-цифрового вольтметра 6 при нагруженных тензодатчиках, определить с помощью индикатора 7 величину прогиба тарировочной балки. Показания занести в таблицу 4.1. ОБРАБОТКА РЕЗУЛЬТАТОВ Исходные данные для расчета: Толщина тарировочной балки Длина тарировочной балки между опорными призмами Наружный диаметр цилиндрической обечайки Dн = 0,42 м Толщина стенки аппарата δ = 4×10-3 м. Модуль Юнга Давление в аппарате задается преподавателем.
Определение процента ошибки Определить процент отклонения по формуле:
где sтеор – расчетное значение напряжений; sэкс – экспериментальное значение напряжения. Все результаты расчетов занести в таблицу 4.1.
Таблица 4.1 - Отчетная таблица
КОНТРОЛЬНЫЕ ВОПРОСЫ 1) Какие аппараты называются тонкостенными? 2) Что называется оболочкой, срединной поверхностью? Почему расчет тонкостенных оболочек производится для срединной поверхности? 3) Что называется меридианом и параллелью оболочки? 4) Охарактеризуйте 1-й и 2-й главные радиусы кривизны оболочки? 5) Охарактеризуйте радиус кольцевого сечения оболочки и укажите его связь со 2-м главным радиусом. 6) Что является углом широты оболочки? 7)Какие существуют теории расчета тонкостенных оболочек? Почему они получили такие названия? 8) Какие делаются допущения при расчете тонкостенных оболочек? 10) Охарактеризуйте геометрические параметры конических днищ. 11) Чему равны напряжения в конических днищах, шаровых и на полюсе эллиптических днищ? 12) Как экспериментально и теоретически определить меридиональные и кольцевые напряжения в цилиндрических обечайках? 13)Что влияет на напряженное состояние тонкостенных оболочек? ЛАБОРАТОРНАЯ РАБОТА № 2 ЦЕЛЬ РАБОТЫ Теоретически и экспериментально определить напряжения, действующие на поверхности плоской крышки и плоского днища, для заданных значений внутреннего давления, сравнить экспериментальные значения с расчетными и определить процент отклонения. СОДЕРЖАНИЕ РАБОТЫ Расчет напряжений вплоских круглых крышках или днищах ведется согласно теории тонких пластинок, по которой общие уравнения круглых пластинок, нагруженных симметрично, записываются в дифференциальной форме:
Уравнения изгибающихся моментов записывается в виде:
где Mr – радиальный момент, отнесенный к единице длины; Mt – кольцевой момент, отнесенный к единице длины, φ - угол поворота нормали к срединной поверхности; W – прогиб пластинки на некотором радиусе окружности; r – текущий радиус; Уравнения (2.1) и (2.2) называются уравнениями углов поворота нормалей и прогибов пластинки в дифференциальной форме. Так как способ закрепления крышки или днища по краям (рис. 2.1) влияет на величину и характер распределения этих напряжений, то конструктивную схему можно свести к шарнирной (рис. 2.2) или жестко защемленной (рис. 2.3).
Рис. 2.1.
Рис. 2.2. Рис. 2.3. В действительности же будет иметь место промежуточный случай, тo есть упругая заделка края. Для определения перерезающей силы, независимо от способа заделки края крышки или днища, уравнение равновесия центральной частикрышки радиуса r (рис. 2.4) запишется в виде:
Откуда:
Рис. 2.4. Подставив значение Q в уравнение (2.1) и дважды проинтегрировав его, получим:
где С1 и С2 – постоянные интегрирования. Постоянная интегрирования С2 определяется из условия, что в центре крышки или днища при
Постоянная С1 интегрирования определяется из второго граничного условия при Для жесткозащемленного случая когда при
Для шарнирного закрепления при
Подставим в уравнение (2.10) значение угла поворота нормалей к срединной поверхности
С учетом выражения (2.11) уравнение (2.8) для шарнирного закрепления перепишется:
Подставив в уравнения (2.3), (2.4) значения для жесткого защемления:
для шарнирной заделки:
Нормальные радиальные и кольцевые напряжения, действующие на поверхности плоской крышки или днища, найдутся в общем виде как
Тогда, в зависимости от способа закрепления крышки или днища по контуру, выражения (2.15), (2.16) с учетом (2.13), (2.14) перепишутся в виде: для жесткого защемления:
для шарнирной заделки:
3 ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ И МЕТОДИКАПРОВЕДЕНИЯ ЭКСПЕРИМЕНТА
Рис. 3.1. Расстояние по радиусу от центра крышки (днища) до исследуемой точки r1, r2, r3, r4 замерить на установке и занести в таблицу 4.2. Переключая тумблер 13 из положения 0 в положение 9 снять показания тензостанции при ненагруженных тензодатчиках 5 с помощью электронно-цифрового вольтметра 7 изанести эти показания таблицу 4.2. Закрыть вентиль 14. Создать давление в аппарате, снять показания на манометре 4 до заданного значения давления; но не свыше 3 МПа. Снять показания тензостанции с помощью электронного цифрового вольтметра 7, переключая тумблер 13 из положения 9 в положение 0. Открыть вентиль 14, сбросить давление в аппарате 1 и выдержать 5 минут. Повторить испытание и, если показания не совпадают, подрегулировать каналы. Переключая тумблер 13, нагружать тарировочную балку 10 нагрузкой, величина которой должна соответствовать показаниям электронно-цифрового вольтметра 7 при нагруженных датчиках. Определить с помощью индикатора 8 величину прогиба тарировочной балки 10. ОБРАБОТКА РЕЗУЛЬТАТОВ Исходные данные для расчетов: Толщина тарировочной балки Модуль Юнга Длина тарировочной балки между нижними опорными призмами Коэффициент Пуассона для металлов μ = 0,3 м/м. Давление в аппарате задается преподавателем, но не более 3 МПа.
Таблица 4.1 - Исходные данные для расчетов
Определение процента ошибки Определить отклонения по формуле:
 (4.2) (4.2)
где sтеор - расчетное значение напряжения; sэкс - экспериментальное значение напряжения. Результаты расчетов занести в таблицу 4.2.
Таблица 4.2 - Отчетная таблица
ЛАБОРАТОРНАЯ РАБОТА № 3 СОДЕРЖАНИЕ РАБОТЫ Гидравлическому испытанию подлежат все сосуды и аппараты после их изготовления, а также периодически при их эксплуатации. Гидравлическое испытание сосудов, аппаратов и их элементов должно производиться пробным давлением, указанным в таблице 1. Обычно, эти данные наносятся на чертеж общего вида аппарата. Трубопроводы, по которым транспортируются материалы, участвующие в технологическом процессе, называются технологическими.
Таблица 2.1 - Нормы пробного давления при гидравлическом испытании
где σ20 – допустимое напряжение для материала сосуда или его элементов при температуре стенки 20°С, МПа (×10 кгс/см2); σt – допустимое напряжение для материала сосуда или его элементов при расчетной температуре стенки, [ МПа ] (×10 кгс/см2). Отношение σ20 /σt принимается по тому из применяемых материалов элементов сосуда, для которого оно является наименьшим. Для сосудов высотой более 8 м внутренний осмотр и гидравлическое испытание могут производиться в горизонтальном положении. При этом пробное давление следует принимать с учетом гидростатического давления в рабочих условиях. Сосуды, работающие только под гидростатическим давлением (избыточное давление р=0), подвергаются испытанию наливом водой на всю их высоту.
Таблица 2.2 - Время выдержки сосуда под пробным давлением
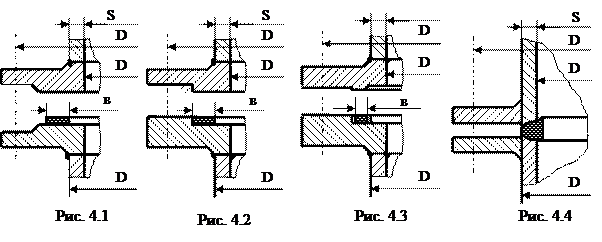
К технологическим трубопроводам не относятся трубопроводы пожарного водопровода, санитарно-технические и трубопроводы систем контроля и автоматики. В зависимости от давления транспортируемой среды трубопроводы делятся на вакуумные, низкого давления (0,1-1,5 МПа (1-15 кгс/см2)), среднего давления (1,6-10 МПа (16-100 кгс/см2)), высокого давления (свыше 10 МПа (100 кгс/см2)) и безнапорные, т.е. работающие без избыточного давления. Транспортируемые по трубопроводам продукты по степени агрессивности разделяются на следующие: 1) неагрессивные и малоагрессивные, вызывающие коррозию, скорость которой не превышает 0,1 мм в год; 2) среднеагрессивные, вызывающие коррозию, скорость которой находится в пределах от 0,1 до 0,5 мм в год; 3) высокоагрессивные, вызывающие коррозию со скоростью выше 0,5 мм в год. В зависимости от условий эксплуатации: температуры, давления, химических свойств транспортируемых продуктов и др. технологические трубопроводы изготовляются из различных материалов. Углеродистые стали применяют для изготовления трубопроводов, транспортирующих малоагрессивные среды с температурой до 450°С, легированные – для продуктов с высокой химической активностью и температурой выше 450°С, чугун применяют в основном для изготовления арматуры и фасонных изделий. Для транспортировки высокоагрессивных продуктов применяют трубы из цветных металлов и сплавов, алюминия, свинца, стекла и пластических масс. Для изменения направления потока или диаметра трубопровода предназначены фасонные детали (к ним относятся отводы, переходы, тройники, крестовины и компенсаторы). Для соединения труб арматуры и других частей трубопровода между собой и с аппаратами предназначены соединительные детали – фланцы. Тип фланца определяется в зависимости от условного прохода и давления.
К трубопроводной арматуре относятся устройства для включения, отключения, изменения количества, давления или направления протекающих по трубопроводам продуктов, указания и регулирования уровня жидкости, а также для автоматического удаления конденсата. В зависимости от назначения арматура подразделяется на следующие виды: краны, вентили, задвижки, обратные, предохранительные, перепускные, регулирующие и аварийные клапаны, конденсатоотводчики. При выборе арматуры учитываются те же условия, что и для трубопроводов. Основные параметры трубопроводов 1. dу (условный проход) – это номинальный внутренний диаметр изделия по присоединительным концам. 2. Ру (условное давление) – давление, на которое рассчитана труба, арматура или соединительная часть трубопровода, при температуре рабочего продукта 00С, условно принятое за основное, при определении допустимых наибольших рабочих давлений. 3. Рраб (рабочее давление) – номинальное эксплуатационное давление транспортируемого продукта, на которое рассчитывается трубопровод. Для стальных труб, арматуры и соединительных частей, работающих при температуре продукта от 0 до 2000С, а также изделий из чугуна, бронзы, латуни, работающих при температуре от 0 до 1200C, рабочее давление равно условному. При более высоких температурах Ру > Рраб. 4. Рпр (пробное давление) – избыточное давление, при котором трубы, арматура и соединительные части трубопроводов должны испытываться на прочность и плотность.
ОБРАБОТКА РЕЗУЛЬТАТОВ
(4.1)
где V – расход жидкости, м3/час; υ – скорость течения жидкости, м/сек. 2) Толщина стенки стальных труб определяется по формуле: δ = δ р + С, (4.2) где δ р – расчётная толщина стенки, мм. δ р = (Р0·Dв) / (2 [σ]φ - Р0) (4.3) 3) Расчётная сила осевого сжатия Рс определяется по формуле: при Р0 > 10 МПа (100 кгс/см2) Рс ≥ π · Dср· вэ· Ратм (4.5) где Dср – средний диаметр уплотнения, мм; вэ – эффективная ширина касания линзы; Р0 – расчётное давление в аппарате, МПа; к – коэффициент, зависящий от материала и конструкции прокладки. Dср=Dв+в/2; вэ=3,8 4) Определим растягивающее усилие в болтах (шпильках) РБ:
где P – расчётная сила от давления внутри аппарата [ кг/см2 ]; Pс – расчётная сила осевого сжатия. 5) Диаметр окружности болтов определяется по формуле: Dб = ψ·Dв0,933 (4.8) где D в – внутренний диаметр фланца, мм; ψ - коэффициент, величина которого выбирается в зависимости от величины P0. При Р 0 ≤ 16 атм, ψ = 1,11. 6) Расчётный диаметр болтов определяется по формуле:
где Dг – диаметр горловины фланца, мм. (DГ= DВ). 7) Расчётное количество болтов определяется по формуле:
где Fб – площадь поперечного сечения болта по внутреннему диаметру резьбы мм2; [σ] – допустимое напряжение на растяжение в болтах при рабочей температуре болтов.
Экспериментальные и расчётные данные сводятся в таблицу 5. Таблица 5 - Отчетная таблица
КОНТРОЛЬНЫЕ ВОПРОСЫ 1) Дать определение технологического трубопровода. 2) Какие характеристические условия влияют на выбор материала трубопровода и его конструкцию? 3) Какие конструктивные и технологические параметры сосудов и аппаратов подлежит расчету и испытанию? 4) Привести подробную методику порядка гидроиспытания. 5) В чем заключается методика расчета на прочность, плотность и герметичность технологических трубопроводов? 6) Классификация трубопроводов по различным критериям. 7) Какими условиями определяется время испытания?
ЛАБОРАТОРНАЯ РАБОТА № 4 ЦЕЛЬ РАБОТЫ Изучение конструкции и принципа работы изотермического реактора периодического действия с мешалкой, опытное и теоретическое определение мощности, затрачиваемой на перемешивание. СОДЕРЖАНИЕ РАБОТЫ Во всех реакторах имеют место определенные физические процессы (гидродинамческие, тепловые и диффузионные), с помощью которых создаются оптимальные условия проведения химических процессов. Для осуществления физических этапов процесса химические реакторы имеют в своей структуре простые аппараты или элементы аппаратов:мешалки;теплообменники;контактные устройства (тарелки, насадки и т.д.).Таким образом, химический реактор можно рассматривать как комплексный аппарат, состоящий из определенных сочетаний простых аппаратов или элементов аппаратов. Наиболее часто химические реакторы классифицируют по следующим критериям: непрерывность работы; тепловой режим и режим движения реакционной среды; фазовое состояние реаген
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1991; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.152.151 (0.015 с.) |

 В этом случае напряженное состояние тонкостенных аппаратов можно считать плоским.
В этом случае напряженное состояние тонкостенных аппаратов можно считать плоским.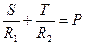 (2.1)
(2.1) (2.2)
(2.2) ACK = φ - угол широты, т.е. угол между 1-м главным радиусом и осью вращения оболочки.
ACK = φ - угол широты, т.е. угол между 1-м главным радиусом и осью вращения оболочки.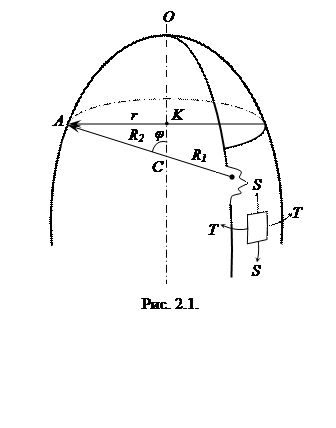

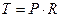 и
и 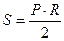 . (2.3)
. (2.3)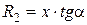 , радиус кольцевого сечения r является переменной величиной, а угол широты φ=(π/2 – α).
, радиус кольцевого сечения r является переменной величиной, а угол широты φ=(π/2 – α).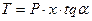 ,
, 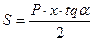 . (2.4)
. (2.4) ), а радиус кольцевого сечения r и угол широты
), а радиус кольцевого сечения r и угол широты  являются переменными величинами:
являются переменными величинами: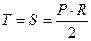 . (2.5)
. (2.5)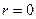 ,
, 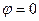 и
и  (рис.2.3) меридиональные и кольцевые силы равны между собой:
(рис.2.3) меридиональные и кольцевые силы равны между собой: (2.6)
(2.6)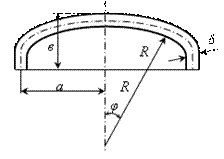
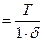 и ss
и ss  , (2.7)
, (2.7) , (2.8)
, (2.8)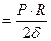 . (2.9)
. (2.9) , (2.10)
, (2.10) , (2.11)
, (2.11) . (2.12)
. (2.12)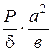 (2.13).
(2.13). Схема экспериментальной установки представлена на рисунке 3.1.
Схема экспериментальной установки представлена на рисунке 3.1.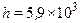 м.
м. м.
м.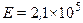 МПа.
МПа. (4.2)
(4.2) (2.1)
(2.1) (2.2)
(2.2) (2.3)
(2.3) (2.4)
(2.4)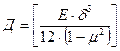 - цилиндрическая жесткость пластины; Е – модуль упругости первого рода;
- цилиндрическая жесткость пластины; Е – модуль упругости первого рода; 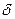 - толщина пластинки;
- толщина пластинки;  - коэффициент Пуассона; Q – перерезывающая сила.
- коэффициент Пуассона; Q – перерезывающая сила.

 . (2.5)
. (2.5) . (2.6)
. (2.6)
 (2.7)
(2.7) , а это возможно только в том случае, когда С2=0 в уравнении (2.7). Следовательно, уравнение (2.7) можно представить в виде:
, а это возможно только в том случае, когда С2=0 в уравнении (2.7). Следовательно, уравнение (2.7) можно представить в виде: (2.8)
(2.8) и зависит от способа закрепления крышки по контуру.
и зависит от способа закрепления крышки по контуру. , из уравнения (2.8) имеем, что
, из уравнения (2.8) имеем, что  . Тогда уравнение (2.8) перепишется:
. Тогда уравнение (2.8) перепишется: (2.9)
(2.9) и из уравнения (2.3) имеем:
и из уравнения (2.3) имеем: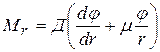 (2.10)
(2.10) ,а затем, решим его относительно С1.
,а затем, решим его относительно С1. (2.11)
(2.11)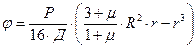 (2.12)
(2.12)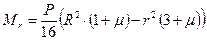 (2.13)
(2.13) ,
,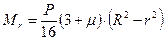 (2.14)
(2.14)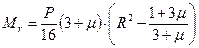 .
. (2.15)
(2.15)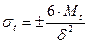 (2.16)
(2.16) (2.17)
(2.17) (2.18)
(2.18) (2.19)
(2.19) (2.20)
(2.20) Схема экспериментальной установки представлена на рисунке 3.1. Основным элементом является тонкостенный цилиндрический аппарат 1, снабженный плоской разъемной крышкой 2 и плоским приварным днищем 3. Рабочее давление в аппарате 1, заполненным касторовым маслом, создается грузопоршневым манометром 4 (МП-600). Под действием давления в материале плоской крышки и плоского днища возникают деформации, которые воспринимаются тензодатчиками 5, наклеенными на наружной поверхности. Сигнал от тензодатчиков поступает на тензостанцию 6 («Топаз 3-4-01») и регистрируется электронным цифровым вольтметром 7 (В7-20). После снятия рабочего давления в аппарате 1 с помощью индикатора часового типа 8, установленного на тарировочном устройстве 9, по показаниям электронного цифрового вольтметра 7 определяется прогиб балки 10, на которой наклеены компенсационные датчики 11 и 12.
Схема экспериментальной установки представлена на рисунке 3.1. Основным элементом является тонкостенный цилиндрический аппарат 1, снабженный плоской разъемной крышкой 2 и плоским приварным днищем 3. Рабочее давление в аппарате 1, заполненным касторовым маслом, создается грузопоршневым манометром 4 (МП-600). Под действием давления в материале плоской крышки и плоского днища возникают деформации, которые воспринимаются тензодатчиками 5, наклеенными на наружной поверхности. Сигнал от тензодатчиков поступает на тензостанцию 6 («Топаз 3-4-01») и регистрируется электронным цифровым вольтметром 7 (В7-20). После снятия рабочего давления в аппарате 1 с помощью индикатора часового типа 8, установленного на тарировочном устройстве 9, по показаниям электронного цифрового вольтметра 7 определяется прогиб балки 10, на которой наклеены компенсационные датчики 11 и 12. .
. .
. .
.


 1) Определить расчётный внутренний диаметр трубопровода по формуле:
1) Определить расчётный внутренний диаметр трубопровода по формуле: .
. (4.6)
(4.6) (4.7)
(4.7) (4.9)
(4.9) (4.10)
(4.10) . (4.11)
. (4.11)


