
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оболочках, работающих под действием внутреннего давленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Корпуса химических аппаратов состоят из обечаек и днищ и, как правило, изготавливаются из одного и того же материала. Под действием внутреннего давления стенки аппарата находятся в объемном напряженном состоянии, когда вдоль образующей действует меридиональное (осевое) напряжение ss, по касательной окружности – кольцевое напряжение st и по нормам к стенке – радиальное напряжение sr . Все три напряжения являются нормальными и главными, так как они действуют в сечении, в котором отсутствуют касательные напряжения. Особенностью расчета тонкостенных аппаратов, у которых толщина стенки много меньше диаметра, является то, что можно пренебречь радиальными напряжениями sr, величина которых невелика и по абсолютному значению не превышает давление среды в аппарате, т.е. sr @ 0. Исходя из другого допущения, что напряжения ss, и st равномерно распределяются по толщине стенки, можно предположить, что отсутствует изгиб оболочки, и основанная на этом предположении теория расчета называется безмоментной или мембранной. ЦЕЛЬ РАБОТЫ Исследовать напряженное состояние тонкостенных оболочек различной формы, находящихся под действием внутреннего давления. СОДЕРЖАНИЕ РАБОТЫ Оболочкой называется тело, ограниченное двумя криволинейными поверхностями, расстояние между которыми мало по сравнению с другими размерами. Геометрическое место точек, равноотстоящих от обеих поверхностей оболочки, носит название срединной поверхности. При расчете тонкостенных оболочек все нагрузки, действующие на них, прикладывают к срединной поверхности оболочки. Если срединная поверхность оболочки является плоскостью, то такую оболочку называют пластиной. Если срединная поверхность оболочки образует поверхность вращения в форме цилиндра, то оболочку называют цилиндрической. Меридианом называется линия пересечения срединной поверхности с плоскостью, проходящей через ось вращения оболочки (ОАВ). Параллелью называется линия пересечения срединной поверхности с поверхностью, перпендикулярной к меридиану (АА1А2). Кольцевым сечением называется сечение, перпендикулярное оси вращения оболочки и проходящее через ее параллель. Существует две теории определения напряжений в тонкостенных аппаратах: моментная и безмоментная (мембранная). В местах, удаленных на некоторое расстояние от линии сопряжения тонкостенных оболочек различной формы, расчет напряжений целесообразно производить по более простой безмоментной теории, расчетные формулы которой справедливы для срединной поверхности. Основные положения безмоментной теории заключаются в следующем: 1) нагрузки, действующие на поверхности оболочки, могут считаться перпендикулярными им и симметричными относительно оси вращения оболочки; 2) вследствие малой толщины оболочки сопротивление изгибу отсутствует (изгибающий момент не возникает); 3) напряжения по толщине стенки оболочки распределены равномерно. Основными уравнениями безмоментной теории расчета являются уравнение Лапласа (уравнение 2.1) и уравнение равновесия зоны оболочки (уравнение 2.2), которые для аппаратов, нагруженных внутренним газовым давлением Р,соответственно запишутся соответственно:
где АС1=R1 – радиус кривизны меридиана или 1-й главный радиус, м; АС=R2 – радиус кривизны меридиана или 2-й главный радиус, м; АК=r – радиус кольцевого сечения оболочки, м;
Характерными геометрическими параметрами конических днищ является половина угла раскрытия конуса a и расстояние х от вершины конуса до исследуемой точки (рис. 2.2).
Учитывая, что для цилиндрической обечайки радиус кривизны меридиана R1 = ∞, а R2 = r = R (радиус срединной поверхности цилиндра), и угол широты φ = π/2, из уравнения (2.1) и (2.2) получим:
где S - меридиональная сила, т.е. сила, действующая на единицу длины параллельного круга, на всю толщину оболочки и лежащая в плоскости меридиана, Н/м (рис. 2.1); Т - кольцевая сила, т.е. сила действующая на единицу длины меридиана, на всю толщину оболочки и лежащая в плоскости параллели, Н/м. В случае газового давления величина давления постоянная во всех точках поверхности оболочки. Для резервуаров, наполненных жидкостью, давление по их высоте переменно. В этом случае необходимо учитывать, что если на какую-либо поверхность действует давление жидкости, то вертикальные составляющие сил давления равны весу жидкости в объеме, расположенном над поверхностью. Поэтому давление жидкости в различных сечениях оболочки будет различным в отличие от давления газа. Для конического днища имеем: R1 =∞, В этом случае: Для полушаровых днищ, у которых радиус является радиусом срединной поверхности шара (
На полюсе эллиптических днищ при
где а – большая полуось эллипса; в – малая полуось эллипса.
Рис. 2.3. Кольцевые и меридиональные напряжения, отнесенные к единице длины, в общем случае запишутся в виде выражений: st где δ - толщина оболочки, м. Тогда для любой формы тонкостенных оболочек, нагруженных внутренним давлением Р, имеем для цилиндрических обечаек: st ss Для конических днищ: st ss где xt и xs – расстояние от вершины конического днища до центра наклейки кольцевого и меридионального датчиков соответственно. Для шаровых днищ: st=ss На полюсе эллиптических днищ: st=ss= 3 ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ И МЕТОДИКАПРОВЕДЕНИЯ ЭКСПЕРИМЕНТА
Рис. 3.1 Основным элементом является горизонтальный цилиндрический аппарат. Рабочее давление в аппарате, заполненном касторовым маслом, создается грузопоршневым манометром 2 (МП-600). Под действием внутреннего давления в цилиндрической обечайке возникают деформации, которые воспринимаются тензодатчиками 3, наклеенными на наружной поверхности тонкостенной оболочки по кольцу и вдоль образующих. Сигнал от тензодатчиков через тарировочное устройство 4 («УТС-1») усиливается тензостанцией 5 («ТОПАЗ 3-4-01») и регистрируется электронно-цифровым вольтметром 6 («В7-20»). После снятия рабочего давления в аппарате с помощью индикатора часового типа 7, установленного на тарировочном устройстве 4, по показаниям электронно-цифрового вольтметра 6 определяется прогиб тарировочной балки 8, на которой наклеены компенсационные датчики 9, 10. С помощью электронно-цифрового вольтметра 6 снять показания с тензостанции 5 при ненагруженных тензодатчиках 3 и данные занести в таблицу 4.1. Закрыть вентиль 11 и нагрузить аппарат грузопоршневым манометром 2 до заданного значения внутреннего давления. Снять показания с тензостанции 5 с помощью электронно-цифрового вольтметра 6 и данные занести в таблицу 4.1. Открыть вентиль 11, сбросить давление в аппарате и выдержать 5 минут. Повторить испытание и, если показания не совпадают, подрегулировать каналы тензостанции 5. Создавая на тарировочной балке 8 нагрузку, величина которой должна соответствовать показаниям электронно-цифрового вольтметра 6 при нагруженных тензодатчиках, определить с помощью индикатора 7 величину прогиба тарировочной балки. Показания занести в таблицу 4.1. ОБРАБОТКА РЕЗУЛЬТАТОВ Исходные данные для расчета: Толщина тарировочной балки Длина тарировочной балки между опорными призмами Наружный диаметр цилиндрической обечайки Dн = 0,42 м Толщина стенки аппарата δ = 4×10-3 м. Модуль Юнга Давление в аппарате задается преподавателем.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 497; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.009 с.) |

 В этом случае напряженное состояние тонкостенных аппаратов можно считать плоским.
В этом случае напряженное состояние тонкостенных аппаратов можно считать плоским.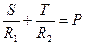 (2.1)
(2.1) (2.2)
(2.2) ACK = φ - угол широты, т.е. угол между 1-м главным радиусом и осью вращения оболочки.
ACK = φ - угол широты, т.е. угол между 1-м главным радиусом и осью вращения оболочки.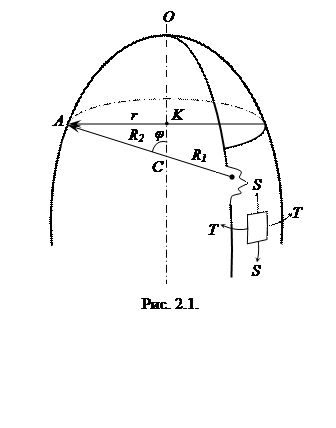

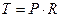 и
и 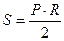 . (2.3)
. (2.3)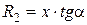 , радиус кольцевого сечения r является переменной величиной, а угол широты φ=(π/2 – α).
, радиус кольцевого сечения r является переменной величиной, а угол широты φ=(π/2 – α).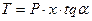 ,
, 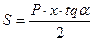 . (2.4)
. (2.4) ), а радиус кольцевого сечения r и угол широты
), а радиус кольцевого сечения r и угол широты  являются переменными величинами:
являются переменными величинами: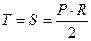 . (2.5)
. (2.5)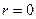 ,
, 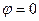 и
и  (рис.2.3) меридиональные и кольцевые силы равны между собой:
(рис.2.3) меридиональные и кольцевые силы равны между собой: (2.6)
(2.6)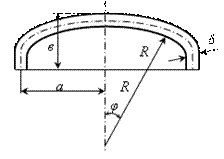
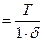 и ss
и ss  , (2.7)
, (2.7) , (2.8)
, (2.8)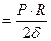 . (2.9)
. (2.9) , (2.10)
, (2.10) , (2.11)
, (2.11) . (2.12)
. (2.12)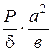 (2.13).
(2.13). Схема экспериментальной установки представлена на рисунке 3.1.
Схема экспериментальной установки представлена на рисунке 3.1.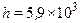 м.
м.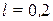 м.
м.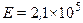 МПа.
МПа.


