
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Допущения, связанные со свойствами материаловСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Вопрос Механические свойства материалов совокупность показателей, характеризующих сопротивлениематериала воз действующей на него нагрузке, его способность деформироваться при этом, а такжеособенности его поведения в процессе разрушения. Диаграмма деформации. Приложенная к образцу нагрузка вызывает его деформацию (См.Деформация). Соотношения между нагрузкой и деформацией описываются т. н. диаграммой деформации(рис. 2). Вначале деформация образца (при растяжении — приращение длины Δ l) пропорциональнавозрастающей нагрузке Р, затем в точке n эта пропорциональность нарушается, однако для увеличениядеформации необходимо дальнейшее повышение нагрузки Р; при Δ l > Δ l в деформация развивается безприложения усилия извне, при постепенно падающей нагрузке. Вид диаграммы деформации не меняется,если по оси ординат откладывать напряжение
а по оси абсцисс — относительное удлинение
(F0 и l0 — соответственно начальная площадь поперечного сечения и расчётная длина образца). Сопротивление материалов измеряется напряжениями, характеризующими нагрузку, приходящуюся наединицу площади поперечного сечения образца
в кгс / мм2. Напряжение
при котором нарушается пропорциональный нагрузке рост деформации, называется пределомпропорциональности. При нагрузке Р < Рn разгрузка образца приводит к исчезновению деформации,возникшей в нём под действием приложенного усилия; такая деформация называется упругой. Небольшоепревышение нагрузки относительно Рn может не изменить характера деформации — она по-прежнемусохранит упругий характер. Наибольшая нагрузка, которую выдерживает образец без появления остаточнойпластической деформации при разгрузке, определяет предел упругости материала:
У конструкционных неметаллический материалов (пластмассы, резины) приложенная нагрузка можетвызвать упругую, высокоэластическую и остаточную деформации. В отличие от упругой,высокоэластическая деформация исчезает не сразу после разгрузки, а с течением времени. Высокопрочныеармированные полимеры (стеклопластики, углепластики и др.) разрушаются при удлинении 1—3%. Напоследних стадиях нагружения у некоторых армированных полимеров появляется высокоэластическаядеформация. Высокоэластический модуль ниже модуля упругости, поэтому диаграмма деформации в этомслучае имеет тенденцию отклоняться к оси абсцисс. Упругие свойства. В упругой области напряжение и деформация связаны коэффициентомпропорциональности. При растяжении σ = Еδ, где Е — т. н. модуль нормальной упругости, численно равныйтангенсу угла наклона прямолинейного участка кривой σ = σ(δ) к оси деформации (рис. 2). При испытаниина растяжение цилиндрического или плоского образца одноосному (σ1>0; (σ2 = σ3 = 0) напряжённомусостоянию соответствует трёхосное деформированное состояние (приращение длины в направлениидействия приложенных сил и уменьшение линейных размеров в двух других взаимно перпендикулярныхнаправлениях): δ1>0; δ2 = δ3 < 0. Соотношение между поперечной и продольной деформацией(коэффициент Пуассона)
в пределах упругости для основных конструкционных материалов колеблется в довольно узкихпределах (0,27—0,3 для сталей, 0,3—0,33 для алюминиевых сплавов). Коэффициент Пуассона являетсяодной из основных расчётных характеристик. Зная μ и Е, можно расчётным путём определить и модульсдвига
и модуль объёмной упругости
Для определения Е, G, и μ пользуются Тензометрами. Сопротивление пластической деформации. При нагрузках Р > Рв наряду со всё возрастающейупругой деформацией появляется заметная необратимая, не исчезающая при разгрузке пластическаядеформация. Напряжение, при котором остаточная относительная деформация (при растяжении —удлинение) достигает заданной величины (по ГОСТ — 0,2 %), называется условным пределом текучести иобозначается
Практически точность современных методов испытания такова, что σп и σе определяют с заданнымидопусками соответственно на отклонение от закона пропорциональности [увеличение ctg(90 — α) на 25—50%] и на величину остаточной деформации (0,003—0,05 %) и говорят об условных пределахпропорциональности и упругости. Кривая растяжения конструкционных металлов может иметь максимум(точка в на рис. 2) или обрываться при достижении наибольшей нагрузки Рв ’. Отношение
характеризует временное сопротивление (предел прочности) материала. При наличии максимума накривой растяжения в области нагрузок, лежащих на кривой левее в, образец деформируется равномерно повсей расчётной длине l 0, постепенно уменьшаясь в диаметре, но сохраняя начальную цилиндрическую илипризматическую форму. При пластической деформации металлы упрочняются, поэтому, несмотря науменьшение сечения образца, для дальнейшей деформации требуется прикладывать всё возрастающуюнагрузку. σв, как и условные σ0,2, σn и σе, характеризует сопротивление металлов пластическойдеформации. На участке диаграммы деформации правее в форма растягиваемого образца изменяется:наступает период сосредоточенной деформации, выражающейся в появлении «шейки». Уменьшениесечения в шейке «обгоняет» упрочнение металлов, что и обусловливает падение внешней нагрузки научастке Рв — Pk. У многих конструкционных материалов сопротивление пластической деформации в упруго-пластической области при растяжении и сжатии практически одинаково. Для некоторых металлов и сплавов(например, магниевые сплавы, высокопрочные стали) характерны заметные различия по этойхарактеристике при растяжении и сжатии. Сопротивление пластической деформации особенно часто (приконтроле качества продукции, стандартности режимов термической обработки и в др. случаях) оцениваетсяпо результатам испытаний на твёрдость путём вдавливания твёрдого наконечника в форме шарика(твёрдость по Бринеллю или Роквеллу), конуса (твёрдость по Роквеллу) или пирамиды (твёрдость поВиккерсу). Испытания на твёрдость не требуют нарушения целостности детали и потому являются самыммассовым средством контроля механических свойств. Твёрдость по Бринеллю (HB) при вдавливании шарикадиаметром D под нагрузкой Р характеризует среднее сжимающее напряжение, условно вычисляемое наединицу поверхности шарового отпечатка диаметром d:
Характеристики пластичности. Пластичность при растяжении конструкционных материаловоценивается удлинением
или сужением
при сжатии — укорочением
(где h0 и hk — начальная и конечная высота образца), при кручении — предельным угломзакручивания рабочей части образца Θ, рад или относительным сдвигом γ = Θ r (где r — радиус образца).Конечная ордината диаграммы деформации (точка k на рис. 2) характеризует сопротивление разрушениюметалла Sk, которое определяется
(Fk — фактическая площадь в месте разрыва). Характеристики разрушения. Разрушение происходит не мгновенно (в точке k), а развивается вовремени, причём начало в разрушения может соответствовать какой-то промежуточной точке на участке вк,а весь процесс заканчиваться при постепенно падающей до нуля нагрузке. Положение точки к на диаграммедеформации в значительной степени определяется жёсткостью испытательной машины ииннерционностью измерительной системы. Это делает величину Sk в большой мере условной. Многие конструкционные металлы (стали, в том числе высокопрочные, жаропрочные хромоникелевыесплавы, мягкие алюминиевые сплавы и др.) разрушаются при растяжении после значительной пластическойдеформации с образованием шейки. Часто (например, у высокопрочных алюминиевых сплавов) поверхностьразрушения располагается под углом примерно 45° к направлению растягивающего усилия. Приопределенных условиях (например, при испытании хладноломких сталей в жидком азоте или водороде, привоздействии растягивающих напряжений и коррозионной среды для металлов, склонных к коррозии поднапряжением) разрушение происходит по сечениям, перпендикулярным растягивающей силе (прямойизлом), без макропластической деформации. Прочность материалов, реализуемая в элементах конструкций, зависит не только от механическихсвойств самого металла, но и от формы и размеров детали (т. н. эффекты формы и масштаба), упругойэнергии, накопленной в нагруженной конструкции, характера действующей нагрузки (статическая,динамическая, периодически изменяющаяся по величине), схемы приложения внешних сил (растяжениеодноосное, двухосное, с наложением изгиба и др.), рабочей температуры, окружающей среды. Зависимостьпрочности и пластичности металлов от формы характеризуется т. н. чувствительностью к надрезу,оцениваемой обычно по отношению пределов прочности надрезанного и гладкого образцов
(у цилиндрических образцов надрез обычно выполняют в виде круговой выточки, у полос — в видецентрального отверстия или боковых вырезов). Для многих конструкционных материалов это отношение пристатической нагрузке больше единицы, что связано со значительной местной пластической деформацией ввершине надреза. Чем острее надрез, тем меньше локальная пластическая деформация и тем больше доляпрямого излома в разрушенном сечении. Хорошо развитый прямой излом можно получить при комнатнойтемпературе у большинства конструкционных материалов в лабораторных условиях, если растяжению илиизгибу подвергать образцы массивного сечения (тем толще, чем пластичнее материал), снабдив этиобразцы специальной узкой прорезью с искусственно созданной трещиной (рис. 3). При растяженииширокого, плоского образца пластическая деформация затруднена и ограничивается небольшой областьюразмером 2 ry (на рис. 3, б заштрихована), непосредственно примыкающей к кончику трещины. Прямойизлом обычно характерен для эксплуатационных разрушений элементов конструкций. Широкое распространение получили предложенные американским учёным Дж. Р. Ирвином в качествеконстант для условий хрупкого разрушения такие показатели, как критический коэффициент интенсивностинапряжений при плоской деформации K1C и вязкость разрушения
При этом процесс разрушения рассматривается во времени и показатели K1C (G1C) относятся к томукритическому моменту, когда нарушается устойчивое развитие трещины; трещина становится неустойчивойи распространяется самопроизвольно, когда энергия, необходимая для увеличения её длины, меньшеэнергии упругой деформации, поступающей к вершине трещины из соседних упруго напряжённых зонметалла. При назначении толщины образца t и размеров трещины 2 lтр исходят из следующего требования
Коэффициент интенсивности напряжений К учитывает не только значение нагрузки, но и длинудвижущейся трещины:
(λ учитывает геометрию трещины и образца), выражается в кгс / мм3 / 2 или Мн / м3 / 2. По K1C или G1C можно судить о склонности конструкционных материалов к хрупкому разрушению в условиях эксплуатации. Для оценки качества металла весьма распространены испытания на ударный о изгиб призматическихобразцов, имеющих на одной стороне надрез. При этом оценивают ударную вязкость (См. Ударнаявязкость) (в кгс ․ м / см2 или Мдж / м2) — работу деформации и разрушения образца, условно отнесённую кпоперечному сечению в месте надреза. Широкое распространение получили испытания на ударный изгибобразцов с искусственно полученной в основании надреза трещиной усталости. Работа разрушения такихобразцов ату находится в целом в удовлетворительном соответствии с такой характеристикой разрушения,как K1C, и ещё лучше с отношением
Временна́я зависимость прочности. С увеличением времени действия нагрузки сопротивлениепластической деформации и сопротивление разрушению понижаются. При комнатной температуре уметаллов это становится особенно заметным при воздействии коррозионной (коррозия под напряжением)или др. активной (эффект Ребиндера) среды. При высоких температурах наблюдается явление ползучести(См. Ползучесть), т. е. прироста пластической деформации с течением времени при постоянномнапряжении (рис. 4, а). Сопротивление металлов ползучести оценивают условным пределом ползучести —чаще всего напряжением, при котором пластическая деформация за 100 ч достигает 0,2 %, и обозначаютего σ0,2/100. Чем выше температура t, тем сильнее выражено явление ползучести и тем больше снижаетсяво времени сопротивление разрушению металла (рис. 4, б). Последнее свойство характеризуют т. н.пределом длительной прочности, т. е. напряжением, которое при данной температуре вызываетразрушение материала за заданное время (например, σt100, σt1000 и т. д.). У полимерных материаловтемпературно-временная зависимость прочности и деформации выражена сильнее, чем у металлов. Принагреве пластмасс наблюдается высокоэластическая обратимая деформация; начиная с некоторой болеевысокой температуры развивается необратимая деформация, связанная с переходом материала ввязкотекучее состояние. С ползучестью связано и др. важное механическое свойство материалов —склонность к релаксации напряжений, т. е. к постепенному падению напряжения в условиях, когда общая(упругая и пластическая) деформация сохраняет постоянную заданную величину (например, в затянутыхболтах). Релаксация напряжений обусловлена увеличением доли пластической составляющей общейдеформации и уменьшением её упругой части. Если на металл действует нагрузка, периодически меняющаяся по какому-либо закону (например,синусоидальному), то с увеличением числа циклов N нагрузки его прочность уменьшается (рис. 4, в) —металл «устаёт». Для конструкционной стали такое падение прочности наблюдается до N = (2—5) ․106циклов. В соответствии с этим говорят о пределе усталости конструкционной стали, понимая под нимобычно амплитуду напряжения
ниже которой сталь при повторно-переменной нагрузке не разрушается. При |σmin| = |σmax| пределусталости обозначают символом σ-1. Кривые усталости алюминиевых, титановых и магниевых сплавовобычно не имеют горизонтального участка, поэтому сопротивление усталости этих сплавов характеризуютт. н. ограниченными (соответствующими заданному N) пределами усталости. Сопротивление усталостизависит также от частоты приложения нагрузки. Сопротивление материалов в условиях низкой частоты ивысоких значений повторной нагрузки (медленная, или малоцикловая, усталость) не связано однозначно спределами усталости. В отличие от статической нагрузки, при повторно-переменных нагрузках всегдапроявляется чувствительность к надрезу, т. е. предел усталости при наличии надреза ниже пределаусталости гладкого образца. Для удобства чувствительность к надрезу при усталости выражаютотношением
характеризует асимметрию цикла). В процессе уставания можно выделить период, предшествующийобразованию очага усталостного разрушения, и следующий за ним, иногда довольно длительный, периодразвития трещины усталости. Чем медленнее развивается трещина, тем надёжнее работает материал вконструкции. Скорость развития трещины усталости dl / dN связывают с коэффициентом интенсивностинапряжений степенной функцией:
Различают сопротивление термической усталости, когда появляющиеся в материале напряженияобусловлены тем, что в силу тех или иных причин, например из-за формы детали или условий еёзакрепления, возникающие при циклическом изменении температуры тепловые перемещения не могут бытьреализованы. Сопротивление термической усталости зависит и от многих других свойств материала —коэффициентов линейного расширения и температуропроводности, модуля упругости, предела упругости идр. Объект изучения В сопромате главным объектом для расчета является брус, нагруженный системой внешних усилий (сил, моментов и распределенных нагрузок). Для него могут проводиться следующие виды расчетов: 1. на прочность; 2. на жесткость; 3. на устойчивость. Расчет на прочность является основным, т.к. абсолютно все конструкции должны быть прочными. Различают три вида задачи при расчетах на прочность: 1. Проверка на прочность (проверочный расчет); 2. Подбор размеров сечения бруса (проектировочный расчет); 3. Определение грузоподъемности. При расчетах на жесткость определяются деформации бруса и перемещение его сечений, на основании чего делается заключение о жесткости бруса. При невыполнении условия жесткости определяются необходимые размеры сечения. Вопрос Вопрос Вопрос 1. Брус — любое тело, у которого длина значительно больше других размеров. В зависимости от форм продольной оси и поперечных сечений различают несколько видов брусьев: — прямой брус постоянного поперечного сечения (рис. 4.4, а); — прямой ступенчатый брус (рис. 4.4, 6); — криволинейный брус (рис. 4.4, в). 2. Пластина — любое тело, у которого толщина значительноменьше других размеров (рис.4.5). 3. Массив — тело, у которого три размера одного порядка. Вопрос Метод сечений позволяет определить внутренние силы, которые возникают в стержне, находящемся в равновесии под действием внешней нагрузки. Рассмотрим идеально упругий призматический стержень прямоугольного поперечного сечения (рис. 1.2, а). Выделим внутри стержня какие-либо две частицы K и L, расположенные на бесконечно малом расстоянии друг от друга. Для большей наглядности предположим, что между этими частицами имеется некоторая пружинка, удерживающая их на определенном расстоянии друг от друга. Пусть натяжение пружинки равно нулю.
Вопрос Переменное напряжение Alternate stress Напряжения, переменные во времени, возникающие в элементах конструкции под действием нагрузок, переменных по величине или направлению, а также нагрузок, перемещающихся относительно рассматриваемого элемента.
Допускаемое напряжение Allowable stress Экспериментально установленное для рассматриваемого материала предельное значение напряжения, деленное на коэффициент запаса прочности.
Главное напряжение Principal stress Среди множества площадок, которые можно провести через исследуемую точку, имеются три взаимно перпендикулярные площадки, касательные напряжения на которых отсутствуют. Эти площадки и возникающие на них нормальные напряжения называются главными.
Вопрос Растяжение (сжатие) - это вид деформации стержня, при котором происходит изменение его первоначальной длины. Растяжение (сжатие) вызывается внешними силами, действующими вдоль оси стержня z. При этом в любом поперечном сечении стержня возникает только одно внутреннее усилие – продольная сила (N), которая является равнодействующей всех внутренних сил, возникающих в каждой точке этого сечения и направленных параллельно оси стержня. Вопрос Если продольные силы, возникающие в различных поперечных сечениях стержня, неодинаковы, закон их изменения по длине стержня представляется в виде графика N(z), называемого эпюрой продольных сил. Эпюра продольных сил необходима для оценки прочности стержня и строится для того, чтобы найти опасное сечение (поперечное сечение, в котором продольная сила принимает наибольшее значение Вопрос Пусть в результате деформации первоначальная длина стержня l станет равной. l 1. Изменение длины
называется абсолютным удлинением стержня. Отношение абсолютного удлинения стержня к его первоначальной длине называется относительным удлинением (
При растяжении продольная деформация считается положительной, а при сжатии – отрицательной. Поперечные размеры стержня в результате деформирования также изменяются, при этом при растяжении они уменьшаются, а при сжатии – увеличиваются. Если материал является изотропным, то его поперечные деформации равны между собой:
Опытным путем установлено, что при растяжении (сжатии) в пределах упругих деформаций отношение поперечной деформации к продольной является постоянной для данного материала величиной. Модуль отношения поперечной деформации к продольной, называемый коэффициентом Пуассона иликоэффициентом поперечной деформации, вычисляется по формуле:
Для различных материалов коэффициентПуассона изменяется в пределах
Вопрос Для большинства конструкционных материалов между напряжением (
Закон Гука: Напряжение пропорционально деформации. Впервые Закон Гука был опубликован в виде анаграммы английским ученым Робертом Гуком (1635 – 1703 гг.). При правильной расстановке букв анаграмма читается: «Каково удлинение, такова и сила». К такому же заключению в 1680 г., независимо от Гука, пришел французский ученыйЭдмон Мариотт. Коэффициент пропорциональности (E) в формуле закона Гука Необходимо отметить, что некоторые материалы не подчиняются законуГука, например, кожа, ткани. Такие материалы, как, например, чугун, только с некоторым приближением можно считать подчиняющимся закону Гука. Но даже и те материалы, которые подчиняются закону Гука, перестают ему следовать при достижении деформации определенного значения. Из закона Гука видно: чем больше модульЮнга, тем меньше (при том же значении напряжения) деформация материала. Следовательно, модуль продольной упругости характеризует жесткость материала при растяжении (сжатии). Из формулы закона Юнга видно, что модульЮнга измеряется в тех же единицах, что и нормальное напряжение ( Так, например, для всех марок сталей
Вопрос Для большинства конструкционных материалов между напряжением (
Закон Гука: Напряжение пропорционально деформации. Впервые Закон Гука был опубликован в виде анаграммы английским ученым Робертом Гуком (1635 – 1703 гг.). При правильной расстановке букв анаграмма читается: «Каково удлинение, такова и сила». К такому же заключению в 1680 г., независимо от Гука, пришел французский ученыйЭдмон Мариотт. Коэффициент пропорциональности (E) в формуле закона Гука Необходимо отметить, что некоторые материалы не подчиняются законуГука, например, кожа, ткани. Такие материалы, как, например, чугун, только с некоторым приближением можно считать подчиняющимся закону Гука. Но даже и те материалы, которые подчиняются закону Гука, перестают ему следовать при достижении деформации определенного значения. Из закона Гука видно: чем больше модульЮнга, тем меньше (при том же значении напряжения) деформация материала. Следовательно, модуль продольной упругости характеризует жесткость материала при растяжении (сжатии). Из формулы закона Юнга видно, что модульЮнга измеряется в тех же единицах, что и нормальное напряжение ( Так, например, для всех марок сталей Вопрос Механические характеристики материала определяются в результате испытания образца на специальных прессах. Форма образца может быть различной, но чаще всего стержень с участком постоянного поперечного сечения (круглого или прямоугольного) длиной
Современные испытательные машины снабжены записывающим прибором, который при испытании образца автоматически вычерчивает график зависимости между нагрузкой (P) и абсолютным удлинением ( Рассмотрим диаграмму растяжения для стали марки Ст. 3 (рис. 2.3). Эта диаграмма характеризует поведение данного образца, но не материала, из которого он сделан. В начальной стадии испытания, до точки А с ординатой При некотором значении растягивающей силы За точкой C диаграммы удлинение образца начинает расти быстрее нагрузки. Число линий Людерса – Чернова растет, они сливаются друг с другом и, наконец, теряют ясность своих очертаний. Этот участок диаграммы растяжения называется зоной упрочнения. В наивысшей точке диаграммы D при силе равной Сопротивление образца растяжению, после образования шейки, падает и его разрыв происходит в точке K при нагрузке:
При разрыве образца, как правило, появляется поперечная трещина в центре тяжести поперечного сечения (посредине шейки), а остальная часть сечения скалывается под углом Линия разгрузки образца KL оказывается прямой и параллельной начальному участку диаграммы ОА. Следовательно, полная деформация образца состоит из двух частей: упругой, исчезающей после снятия нагрузки, и остаточной (пластической).
Строительные материалы (бетон, цемент) в основном испытывают на сжатие. Дерево испытывают на сжатие как вдоль, так и поперек волокон. Сталь испытывают на сжатие значительно реже, чем на растяжение. Образцы для испытания на сжатие имеют, как правило, форму кругового цилиндра с отношением высоты образца к диаметру не более 3. Для стали Ст. 3 диаграмма сжатия вплоть до предела текучести почти полностью повторяетдиаграмму растяжения , то есть . . Различие начинает сказываться после наступления текучести. Площадка текучести при сжатии менее четко выражена, чем при растяжении. При больших деформациях различие становится особенно ощутимым, и в первую очередь из-за того, что сжатие сопровождается увеличением площади поперечного сечения образца, вследствие чего испытание требует постоянно возрастающей нагрузки.
Следовательно, при сжатии пластичного материала получить такую характеристику, как предел прочности, не представляется возможным. Исследуемый образец, не претерпевая разрушения, расплющивается, и дальнейшее испытание на сжатие ограничивается возможностями пресса. В расчетной практике предел прочности пластичного материала на сжатие условно принимается таким же, как и на растяжение. Диаграмма сжатия хрупкого материала по виду напоминает диаграмму растяжения, но предел прочности на сжатие, как правило, в несколько раз больше, чем на растяжение ( Наглядное представление о сравнительных механических характеристиках низкоуглеродистой стали и серого чугуна при растяжении и сжатии дают диаграммы, показанные на рис. 2.5. Вопрос Применяемые в инженерной практике материалы можно разделить на 2 группы: пластичные, которые разрушаются после появления значительных остаточных деформаций и хрупкие, которые разрушаются при весьма малых деформациях.
Это деление является условным, ибо один и тот же материал в зависимости от характера напряженного состояния, температуры и скорости деформирования может вести себя, как пластичный или как хрупкий. Поэтому при решении задач по сопромату правильнее говорить о пластичном или хрупком состоянии материала.
Основные механические характеристики пластичного материала (например, малоуглеродистой стали) определяются при испытании на растяжение. На рис. 6,а показана типичная диаграмма растяжения образца из малоуглеродистой стали. Диаграмма характеризует поведение данного индивидуального образца с его конкретными размерами. Для того тобы получить механические характеристики исследуемого материала, необходимо исключить влияние абсолютных размеров образца. С этой целью диаграмму перестраивают в координатах
где Ао и l - соответственно начальная площадь поперечного сечения и начальная расчетная длина образца (рис. 6 б).
Характер диаграммы после такой.перестройки сохраняется, изменяется лишь масштаб. Эта диаграмма называется диаграммой растяжения материала или диаграммой напряжений, и ее. ординаты дают величины механических характеристик исследуемого материала. В начальной стадии испытания (до точки А с координатой Fпц) зависимость между силой и удлинением линейна, т.е. справедлив закон Гука. Участок диаграммы ОА называется зоной пропорциональности. При растягивающей силе Fу, почти не отличающейся от Fпц, в образце возникают первые остаточные деформации. Участок 0В - зона упругости. При достижении растягивающей силой значения Fт (точка С) наблюдается рост удлине
|
|||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 590; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |


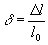

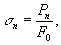
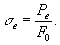



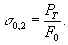

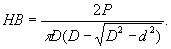

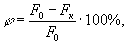
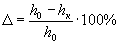



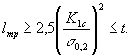




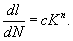
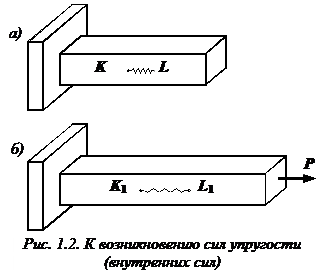 Приложим теперь к стержню растягивающую силу
Приложим теперь к стержню растягивающую силу 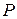 (рис. 1.2, б). Пусть в результате деформации стержня, частица K перейдет в положение
(рис. 1.2, б). Пусть в результате деформации стержня, частица K перейдет в положение 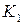 , а частица L – в положение
, а частица L – в положение 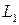 . Соединяющая эти частицы пружинка при этом растянется. После снятия внешней нагрузки частицы вернутся в первоначальное положение K и L благодаря усилию, которое возникло в пружинке. Сила, которая возникла между частицами (в пружинке) в результате деформации идеально упругого стержня, называются силой упругости или внутренней силой. Она может быть найдена методом сечений.
. Соединяющая эти частицы пружинка при этом растянется. После снятия внешней нагрузки частицы вернутся в первоначальное положение K и L благодаря усилию, которое возникло в пружинке. Сила, которая возникла между частицами (в пружинке) в результате деформации идеально упругого стержня, называются силой упругости или внутренней силой. Она может быть найдена методом сечений. ).
).
 – эпсилон) или продольной деформацией. Продольная деформация – это безразмерная величина. Формула безразмерной деформации:
– эпсилон) или продольной деформацией. Продольная деформация – это безразмерная величина. Формула безразмерной деформации: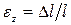
 .
.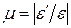
 . Например, для пробки
. Например, для пробки  , для каучука
, для каучука 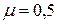 , для стали
, для стали  , для золота
, для золота  .
. ) и продольной деформацией(
) и продольной деформацией(
 МПа.
МПа.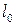 . Концы образца имеют специальные утолщения для их закрепления в испытательной машине.
. Концы образца имеют специальные утолщения для их закрепления в испытательной машине. Перед началом испытания материала на растяжение замеряется площадь поперечного сечения (
Перед началом испытания материала на растяжение замеряется площадь поперечного сечения ( ) средней части образца. Значение растягивающей силы (P) и удлинения его средней части (
) средней части образца. Значение растягивающей силы (P) и удлинения его средней части ( ) в каждый момент нагружения определяются специальными устройствами. При испытании нагрузка увеличивается медленно и плавно.
) в каждый момент нагружения определяются специальными устройствами. При испытании нагрузка увеличивается медленно и плавно. , зависимость между силой (P) и удлинением (
, зависимость между силой (P) и удлинением (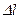 ) носит линейный характер, что свидетельствует о линейной деформируемости образца. Затем диаграмма искривляется и при некотором значении растягивающей силы
) носит линейный характер, что свидетельствует о линейной деформируемости образца. Затем диаграмма искривляется и при некотором значении растягивающей силы  наблюдается значительный рост удлинения образца без увеличения нагрузки (текучесть материала). Практически горизонтальный участок диаграммы BC называется площадкой текучести, а точка B – критической точкой диаграммы.
наблюдается значительный рост удлинения образца без увеличения нагрузки (текучесть материала). Практически горизонтальный участок диаграммы BC называется площадкой текучести, а точка B – критической точкой диаграммы. к оси образца. Далее появляется вторая система линий, пересекающая первую и наклоненную к оси под тем же углом, что и первая. Такая система сопряженных линий называется линиями Людерса – Чернова, представляющие собой следы сдвигов частиц материала. Направления линий Людерса-Чернова соответствует площадкам, на которых при растяжении возникают наибольшие касательные напряжения.
к оси образца. Далее появляется вторая система линий, пересекающая первую и наклоненную к оси под тем же углом, что и первая. Такая система сопряженных линий называется линиями Людерса – Чернова, представляющие собой следы сдвигов частиц материала. Направления линий Людерса-Чернова соответствует площадкам, на которых при растяжении возникают наибольшие касательные напряжения. на образце внезапно появляется местное сужение – шейка, которая представляет собой результат накопления деформаций сдвига.
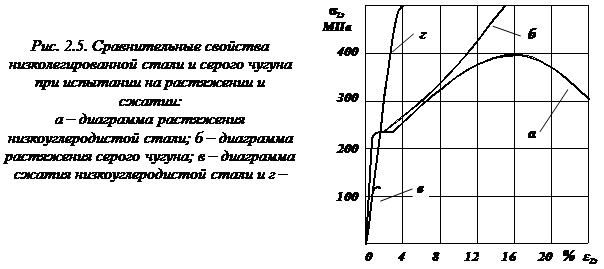
на образце внезапно появляется местное сужение – шейка, которая представляет собой результат накопления деформаций сдвига. .
.
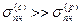 ). Разрушение образца при сжатии происходит обычно путем сдвига одной части относительно другой, происходящим примерно под углом
). Разрушение образца при сжатии происходит обычно путем сдвига одной части относительно другой, происходящим примерно под углом 



