
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Главные напряжения при объемномСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Моменты инерции сечения Рис. 3.3 В дополнение к статическим моментам в системе координат x0y (рис. 3.1)рассмотрим три интегральных выражения:
Первые два интегральных выражения называются севыми моментами инерции относительно осей x и y, а третье - центробежным моментом инерции сечения относительно осей x, y. Для сечений, состоящих из n-числа областей (рис. 3.3), формулы (3.7) по аналогии с (3.6) будут иметь вид:
Рассмотрим, как изменяются моменты инерции сечения при параллельном переносе координатных осей x и y (см. рис. 3.2). Преобразуя формулы (3.7) с учетом выражения (3.2), получим:
Если предположить, что оси x1 и y1 (см. рис. 3.2) являются центральными, тогда и выражения (3.8) упрощаются и принимают вид:
Определим осевые моменты инерции прямоугольника относительно осей x и y, проходящих через его центр тяжести (рис. 3.4). В качестве элементарной площадки dF возьмем полоску шириной b и высотой dy (рис. 3.4). Тогда будем иметь:
Аналогичным образом можно установить, что: Для систем, рассматриваемых в полярной системе координат (рис. 3.5, а), вводится также полярный момент инерции:
где r - радиус-вектор точки тела в заданной полярной системе координат.
Рис. 3.5 Вычислим полярный момент инерции круга радиуса R. На рис. 3.5, a показана элементарная площадка, очерченная двумя радиусами и двумя концентрическими поверхностями, площадью dF = r dr dj. Интегрирование по площади заменим двойным интегрированием:
.Hайдем зависимость между полярным и осевыми моментами инерции для круга. Из геометрии видно (рис. 3.5, б), что r2 = x2 + y2, следовательно,
Так как оси x и y для круга равнозначны, то Ix = Iy = Полярный момент инерции кольца может быть найден как разность моментов инерции двух кругов: наружного (радиусом R) и внутреннего (радиусом r):
10. Главные оси и главные моменты инерции Рассмотрим, как изменяются моменты инерции плоского сечения при повороте осей координат из положения x и y к положению u и v. Из рис. 3.5, б легко установить, что u = y sin a + x cos a; v = y cos a - x sin a. (3.10) Из выражений:
с учетом (3.10) после несложных преобразований получим:
Складывая первые два уравнения, получим: Iu + Iv = Ix + Iy = Ir, (3.12)
Где Дифференцируя в (3.11) выражение Iu по a и приравнивая его нулю, находим значение a = a0, при котором функция Iu принимает экстремальное значение:
С учетом (3.12) можно утверждать, что при a = a0 один из осевых моментов Iu или Iv будет наибольшим, а другой наименьшим. Одновременно при a = a0 Iuv обращается в нуль, что легко установить из третьей формулы (3.11). Декартовы оси координат, относительно которых осевые моменты инерции принимают экстремальные значения, называются главными осями инерции. Осевые моменты инерции относительно главных осей называются главными и определяются из (3.11) с учетом (3.13) и имеют вид:. Момент сопротивления относительно некоторой оси – величина равная мо-менту инерции относительно той же оси отнесенному к расстоянию (ymax или zmax) до наиболее удаленной от этой оси точкиW y= Iy/zmax; Wz=Iz/ymax. Размерность моментов сопротивления метры кубические в СИ Радиусом инерции сечения относительно некоторой оси, называется величи-на, определяемая из соотношения: iz=√Iz/ Fiy=√Iy/F Радиус инерции выражается в м в системе СИ 11 Осевые моменты сопротивления для простейших сечений (Ixc и Iyc - центральные моменты инерции сечений): 1. Для прямоугольника (рис. 4.10).
2. Для треугольника (рис.4.11).
(для верхних волокон). Аналогично можно вычислить моменты сопротивления относительно оси у левых и правых волокон Wул,Wуп 3. Для круга (рис. 4.12).
4. Для полукруга (рис.4.13).
5. Для трубчатого сечения (рис. 4.14).
Полярный момент сопротивления для трубчатого сечения.
12 парал перенос При параллельном переносе осей величины статических моментов меняются. Рассмотрим две пары параллельных осей, x1, y1 и x2, y2.Пусть расстояние между осями x1 и x2 равно b, а между осями y2 и y2 равно а (рис. 2). Положим, что площадь сечения F и статические моменты относительно осей x1 и y1, т. е. Sx1, и Sy1 заданы. Требуется определить Sx2 и Sy2. Очевидно, х2 = x1 — а, y2 = y1 — b. Искомые статические моменты будут равны
Таким образом, при параллельном переносе осей статический момент меняется на величину, равную произведению площади F на расстояние между осями. Рассмотрим более детально, например, первое из полученных выражений:
Величина b может быть любой: как положительной, так и отрицательной. Поэтому ее всегда можно подобрать (причем единственным образом) так, чтобы произведение bF было равно Sx1.Тогда статический момент Sx2, относительно оси x2обращается в нуль.
Рис. 2
Точка пересечения центральных осей называется центром тяжести сечения. Путем поворота осей можно показать, что статический момент относительно любой оси, проходящей через центр тяжести, равен нулю. Нетрудно установить тождественность данного определения и обычного определения центра тяжести как точкиприложения равнодействующих сил веса. Если уподобить рассмотренное сечение однородной пластинке, то сила веса пластинки во всех точках будет пропорциональна элементарной площади dF, а момент сил веса относительно некоторой оси — пропорционален статическому моменту. Этот момент сил веса относительно оси, проходящей через центр тяжести, равен нулю. В нуль обращается, следовательно, и статический момент относительно центральной оси.
Поворот осей ГЛАВНЫЕ ОСИ И ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ Рис. 3
Проектируем замкнутый четырехугольник ОАВСО на оси и и v. Так как проекция ломаной линии равна проекции замыкающей, находим: u = y sin a +x cos a, v = y cos a — x sin a
В выражениях (3), подставив вместо x1 и y1 соответственно u и v, исключаем u и v
откуда
(5)
Рассмотрим два первых уравнения. Складывая их почленно, получим, что сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей не зависит от угла a и при повороте осей остается постоянной. При этом x2 + y2 = r2 где r — расстояние от начала координат до элементарной площадки (рис. 3). Таким образом, Jx + Jy = Jp где Jp— полярный момент инерции
величина которого, естественно, не зависит от поворота осей ху. С изменением угла поворота осей a каждая из величин Ju и Jv меняется, а сумма их остается неизменной. Следовательно, существует такое a, при котором один из моментов инерции достигает своего максимального значения, в то время как другой момент инерции принимает минимальное значение. Дифференцируя выражение Ju (5) по a и приравнивая производную нулю, находим
(6) При этом значении угла a один из осевых моментов будет наибольшим, а другой — наименьшим. Одновременно центробежный момент инерции Juv при указанном угле a обращается в нуль, что легко устанавливается из третьей формулы (5). Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты принимают экстремальные значения, называются главными осями. Если они к тому же являются центральными, то тогда они называются главными центральными осями. Осевые моменты инерции относительно главных осей называются главными моментами инерции. Для определения этого первые две формулы (5) перепишем в виде
Далее исключаем при помощи выражения (6) угол a. Тогда
Верхний знак соответствует максимальному моменту инерции, а нижний — минимальному. После того как сечение вычерчено в масштабе и на чертеже показано положение главных осей, нетрудно установить, которой из двух осейсоответствует максимальный и которой — минимальный момент инерции. Если сечение имеет ось симметрии, то эта ось всегда будет главной.Центробежный момент инерции части сечения, расположенной по одну сторону от оси, будет равен моменту части, расположенной по другую сторону, но противоположен ему по знаку. Следовательно, Jху= 0 и оси х и у являются главными.
14 Удлинение стержня и закон Гука Рассмотрим однородный стержень с одним концом, жестко заделанным, и другим - свободным, к которому приложена центральная продольная сила Р (рис. 2.2). До нагружения стержня его длина равнялась l -после нагружения она стала равной l + Dl (рис. 2.2). Величину Dl называют абсолютным удлинением стержня.
Если же по длине стержня возникает неоднородное напряженное состояние, то для определения его абсолютного удлинения необходимо рассмотреть бесконечно малый элемент длиной dz (рис. 2.2). При растяжении он увеличит свою длину на величину D dz и его деформация составит: Коэффициент Пуассона характеризует упругие свойства материала. При приложении к телу растягивающего усилия оно начинает удлиняться (то есть длина увеличивается), а поперечное сечение уменьшается. Коэффициент Пуассона показывает, во сколько раз изменяется поперечное сечение деформируемого тела при его растяжении или сжатии. Для абсолютно хрупкого материала коэффициент Пуассона равен 0, для абсолютно упругого — 0,5. Для большинства сталей этот коэффициент лежит в районе 0,3, для резины он примерно равен 0,5. (Измеряется в относительных единицах (мм/мм, м/м))
Обобщенный закон Гука Обобщенный закон Гука представляет собой связь между напряжениями и деформациями в случае объемного, и как частый случай, плоского напряженных состояний. Он может быть получен на основании з-на Гука для линейного напряжен состояния и принципа независимости действия сил. Пусть задано произвольное объемное напряж состояние с главными напряжениями
Деформации в направлении действия главных напряжений равны
Эти выражения носят название обобщенного закона Гука, записанного для главных площадок. Деформации Соотношения обобщенного закона Гука могут быть записаны для любых (не главных) площадок, но т.к. при этом будут действовать, кроме нормальных и касательные напряжения (рис.3.10), то необходимо добавить три соотношения для вычисления угловых деформаций. Таким образом, для произвольных площадок обобщенный закон Гука содержит 6 соотношений, связывающих деформации и напряжения:
Чистый сдвиг. Закон гука Чистый сдвиг — это такое напряженное состояние, когда на гранях выделенного из бруса элемента действуют только касательные напряжения. Такие грани называются площадками чистого сдвига. Величина a - абсолютный сдвиг, γ = tg γ = a/h - относительный сдвиг. По аналогии с растяжением – сжатием, закон Гука при сдвиге в абсолютных координатах имеет следующий вид:
где G - модуль сдвига или модуль упругости второго рода. Можно показать, что модуль сдвига связан с модулем упругости первого рода и коэффициентом Пуассона следующим, хорошо согласующимся с опытом, уравнением:
Для стали модуль сдвига G =8·104 МПа. Из уравнения (5.2) с учетом (5.1) может быть получен закон Гука при сдвиге в относительных координатах:
или
Закон Гука справедлив лишь до предела пропорциональности. При испытаниях на сдвиг образцов из пластичных материалов так же, как и при растяжении, наблюдается явление текучести. Предел текучести обозначается через τ т, а предел прочности – через τв.
43 Срез и смятие: общая картина деформации при смятии, условие прочности, допускаемые напряжения Деформация смятия явл. разновидностью деформации сжатия при действии силы на небольшой площади. Возникают напряжения, называющиеся напряжения смятия.1) условие прочности на смятие будет иметь вид:
Смятие материала может происходить в местах сочленения отдельных элементов конструкции. Расчет на смятие необходимо проводить как для разъемных, так и неразъемных соединений; стыковочных узлов, заклепочных соединений, сочленений тяг управления.
Величина допустимых напряжений смятия
44 Расчет заклепок на смятие и листов на разрыв. На практике целый ряд деталей и элементов конструкций работает в таких условиях, что внешние силы стремятся их разрушить именно путем сдвига. В соответствии с этим при проверке прочности таких элементов на первый план выступают касательные напряжения. Простейшими примерами подобных деталей являются болтовые и заклепочные соединения. Заклепки во многих случаях уже вытеснены сваркой; однако они имеют еще очень большое применение для соединения частей всякого рода металлических конструкций: стропил, ферм мостов, кранов, для соединения листов в котлах, судах, резервуарах и т. п. Для образования заклепочного соединения в обоих листах просверливают или продавливают отверстия. В них закладывается нагретый до красного каления стержень' заклепки с одной головкой; другой конец заклепки расклепывается ударами специального молотка или давлением гидравлического пресса (клепальной машины) для образования второй головки. Мелкие заклепки (малого диаметра — меньше 8 мм) ставятся в холодном состоянии (авиационные конструкции).Любое заклепочное соединение работает на 4 вида деформации:-срез заклепок;-срез листа;-разрыв листа;-смятие заклепок;Условия прочности по каждому из видов:1) условие прочности заклепки на перерезывание в таком виде: Рис.1. Передача давлений на стержень заклепки.Чтобы вычислить это условное напряжение смятия, необходимо разделить силу, приходящуюся на заклепку, на площадь диаметрального сечения ВСС'В'. Эта площадь представляет собой прямоугольник, одной стороной которого служит диаметр заклепки, другая же равна толщине листа, передающего давление на стержень заклепки. 45 Кручение: общая картина деформации: скручивающие и крутящие моменты, эпюра крутящих моментов. Кручением называется такой вид деформации, при котором в поперечном сечении стержня возникает лишь один силовой фактор — крутящий момент Мz. Крутящий момент по определению равен сумме моментов внутренних сил относительно продольной оси стержня Oz. Нормальные силы, параллельные оси Oz, вклада в крутящий момент не вносят. С силами, лежащими в плоскости поперечного сечения стержня (интенсивности этих сил — касательные напряжения
47 Деформации бруса круглого сечения. Жесткость при кручении. Эпюра углов закручивания. В любом круговом слое поперечного сечения скручиваемого стержня возникают касательные напряжения
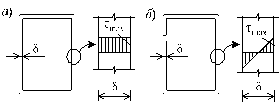
Если в круговом слое скручиваемого стержня обнаружена сдвиговая деформация, то в нем должны возникнуть касательные напряжения, которые по закону Гука составлют τ=Gγ или τ=Gρθ. В центре сеченя напряжения отсутствуют.Относительный угол закручивания пропорционален крутящему моменту в сечении и обратно пропорционален жесткости сечения скручиваемого стержня GIp.Для обеспечения необходимой жесткости производится проверка по условию жесткости вида θmax = Tmax/ (GIp) ≤θadm. Нормативные значения θadm находятся в пределах 0,15 – 2 град/м. 49. Главные напряжения, расчеты на прочность и жесткость, условие прочности. Если скручив. cтержень выполнен из пластичного материала, разрушение происходит от чрезмерных сдвиговых деформаций в поперечных сечениях, развивающихся в поверхностных слоях.Расчетное условие имеет вид: тmax=(Tmax/Ip)ρmax=Tmax/Wp≤RsγcRs – расчётное сопротивление материала сдвигу (Rs=(0.55-0.6)R)Если скручивается стержень из хрупкого материала, то воспользуемся второй теорией прочности (теория наибольших относительных удлинений τmax=Tmax/Wp≤Rtγc/(1+ν), где v – коэффициент Пуассона.Условия прочности при кручении: т=Mzmax/Wp≤[т] Θ=Mzmax/GIp2)Проектный расчет (подбор сечений валов)3)Расчет на грузоподъемность, определяется допускаемая величина крутящего момента.Условие жесткости заключается в том, что угол закручивания единицы длины вала не должен превышать определенную величину.Это условие необходимо учитывать, чтобы избежать явл. пружинения при остановке валов.Допускаемый угол закручивания 1 метра вала Фи0:ФИо≥180*Mz/(Пи*GIp)=ФИ 50. Кручение бруса некруглого поперечного сечения: напряжения, деформации, геометрич. Характеристики, эпюра касательных напряжений для бруса прямоугольного поперечного сечения. Для некруглых поперечных сечений гипотеза плоских сечений неприемлима.Поперечные сечения существенно искривлены и в результате существенно изменяется картина распределения напряжений.Отметим некоторые особенности распределения законов напряжений некруглой формы: 1) если поперечное сечение имеет внешние углы, то в них касательные напряжения должны обращаться в 0 2) если нагруженная поверхность бруса при кручении свободна, то касат. Напряжения, направленные по нормали к контуру так же будут = 0.тA = тmax = Mz/Wk Wk = ρ(b в кубе)Для определения наибольших напряжений и деформаций закручивания пользуются решениями Сен-Ванана:τhmax = T/Wt, Δφ = Tl/(GIt)На рис. 4.3 показана, полученная методом теории упругости, эпюра касательных напряжений для бруса прямоугольного сечения. В углах, как видно, напряжения равны нулю, а наибольшие их значения возникают по серединам больших сторон: в точке А A max = здесь необходимо учесть, что b малая сторона прямоугольника.Значения угла закручивания определяется по формуле: где IK = b 4 аналог полярного момента инерции поперечного сечения бруса.Коэффициенты , и зависят от отношения сторон m = h / b, и их значения приведены в табл. 3. Таблица 3
Характерной геометрической особенностью тонкостенных стержней является то, что их толщина существенно (на порядок и более) меньше других геометрических размеров (длиной срединной линии контура поперечного сечения и длины стержня). Характер распределения напряжений по толщине тонкостенного стержня открытого профиля близок к равномерному (рис. 4.7, б), а замкнутого профиля меняется по линейному закону, как это показано на рис. 4.7, а. Откуда следует, что напряжения в поперечных сечениях открытого профиля практически не изменятся, если профиль сечения распрямить. Иначе говоря, напряжения в криволинейном открытом профиле будут примерно такими же, как и в прямом.Обращаясь к формулам (4.14), (4.16) и при предельном переходе где MK (i) доля крутящего момента, соответствующего i му участку: где угловое перемещение, единое для всех участков: Из условия равновесия сил по оси z выделенного элемента длиной dz (4.9) легко установить, что по контуру сечения произведение является постоянной величиной. С учетом данного обстоятельства, выражение примет вид: где
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 716; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.015 с.) |


 (3.7)
(3.7)
 (3.8)
(3.8) (3.9)
(3.9) Рис. 3.4
Рис. 3.4





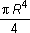 .
.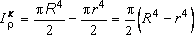
 (3.11)
(3.11) ; Ir - полярный момент инерции сечения, величина которого, как видно, не зависит от угла поворота координатных осей.
; Ir - полярный момент инерции сечения, величина которого, как видно, не зависит от угла поворота координатных осей. (3.13)
(3.13) (3.14)
(3.14)

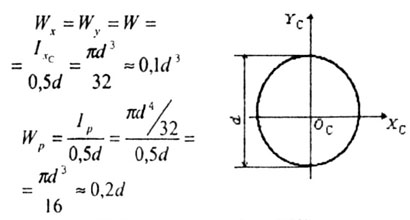






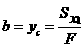 Ось, относительно которой статический момент равен нулю, называется центральной. Среди семейства параллельных осей она является единственной, и расстояние до этой оси от некоторой, произвольно взятой, оси х1равно
Ось, относительно которой статический момент равен нулю, называется центральной. Среди семейства параллельных осей она является единственной, и расстояние до этой оси от некоторой, произвольно взятой, оси х1равно Аналогично для другого семейства параллельных осей
Аналогично для другого семейства параллельных осей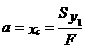
 Посмотрим, как изменяются моменты инерции при повороте осей координат. Положим, даны моменты инерции некоторого сечения относительно осей х, у (не обязательно центральных). Требуется определить Ju, Jv, Juv — моменты инерции относительно осей и, v, повернутых относительно первой системы на угол a (рис. 3).
Посмотрим, как изменяются моменты инерции при повороте осей координат. Положим, даны моменты инерции некоторого сечения относительно осей х, у (не обязательно центральных). Требуется определить Ju, Jv, Juv — моменты инерции относительно осей и, v, повернутых относительно первой системы на угол a (рис. 3).

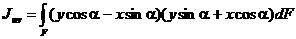


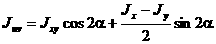



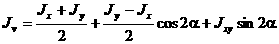

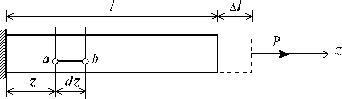 Рис. 2.2 Если в нагруженном стержне напряженное состояние является однородным, т.е. все участки стержня находятся в одинаковых условиях, деформация e остается одной и той же по длине стержня и равной
Рис. 2.2 Если в нагруженном стержне напряженное состояние является однородным, т.е. все участки стержня находятся в одинаковых условиях, деформация e остается одной и той же по длине стержня и равной  (2.1)
(2.1)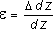 (2.2) В пределах малых деформаций при простом растяжении или сжатии закон Гука записывается в следующем виде:s = E e. (2.3) Величина Е представляет собой коэффициент пропорциональности, называемый модулем упругости материала первого рода. Из совместного рассмотрения уравнений (2.2) и (2.3) получим:
(2.2) В пределах малых деформаций при простом растяжении или сжатии закон Гука записывается в следующем виде:s = E e. (2.3) Величина Е представляет собой коэффициент пропорциональности, называемый модулем упругости материала первого рода. Из совместного рассмотрения уравнений (2.2) и (2.3) получим:  ,откуда с учетом того, что
,откуда с учетом того, что  и
и  ,окончательно получим:
,окончательно получим:  Если стержень изготовлен из однородного изотропного материала с Е = const, имеет постоянное поперечное сечение F = const и нагружен по концам силой Р, то из (2.4) получим
Если стержень изготовлен из однородного изотропного материала с Е = const, имеет постоянное поперечное сечение F = const и нагружен по концам силой Р, то из (2.4) получим  (2.5) При решении многих практических задач возникает необходимость, наряду с удлинениями, обусловленными действием механических нагрузок, учитывать также удлинения, вызванные температурным воздействием. В этом случае пользуются принципом независимости действия сил, и полные деформации рассматривают как сумму силовой и температурной деформаций:
(2.5) При решении многих практических задач возникает необходимость, наряду с удлинениями, обусловленными действием механических нагрузок, учитывать также удлинения, вызванные температурным воздействием. В этом случае пользуются принципом независимости действия сил, и полные деформации рассматривают как сумму силовой и температурной деформаций:  , где a - коэффициент температурного расширения материала; t -перепад температуры тела. Для однородного стержня, нагруженного по концам продольными силами Р и равномерно нагретого по длине, получим:.
, где a - коэффициент температурного расширения материала; t -перепад температуры тела. Для однородного стержня, нагруженного по концам продольными силами Р и равномерно нагретого по длине, получим:.  (2.7)
(2.7)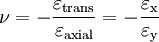 где ν — коэффициент Пуассона.
где ν — коэффициент Пуассона. — деформация в поперечном направлении (отрицательный для осевого растяжения, положительный для осевого сжатия)
— деформация в поперечном направлении (отрицательный для осевого растяжения, положительный для осевого сжатия)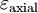 — продольная деформация (положительный для осевого растяжения, отрицательный для осевого сжатия).
— продольная деформация (положительный для осевого растяжения, отрицательный для осевого сжатия).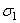 ,
,  и
и 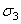 . Представим его в виде суммы 3х линейных напряженных состояний. Учитывая, что при линейном напряженном состоянии
. Представим его в виде суммы 3х линейных напряженных состояний. Учитывая, что при линейном напряженном состоянии  и
и 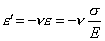 запишем выражение для лин относит деформации в направлении
запишем выражение для лин относит деформации в направлении 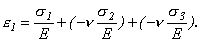
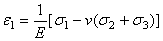 ,
,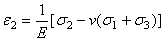 ,
, .
.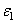 ,
,  ,
, 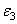 , в направлении главных напряжений называются главными деформациями.
, в направлении главных напряжений называются главными деформациями. ,
,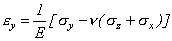 ,
, ,
,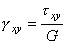 ;
;  ;
;  .
.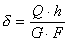 ,
,
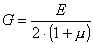 .
.

 .
.
 обусловлена касательным напряжением
обусловлена касательным напряжением  , а деформации
, а деформации  и
и  — соответственно напряжениями
— соответственно напряжениями  и
и  . Между соответствующими касательными напряжениями и угловыми деформациями для линейно-упругого изотропного тела существуют пропорциональные зависимости
. Между соответствующими касательными напряжениями и угловыми деформациями для линейно-упругого изотропного тела существуют пропорциональные зависимости 


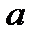 - абсолютный сдвиг,
- абсолютный сдвиг,  - относительный сдвиг.С деформацией сдвига мы встречаемся при резании ножницами металла, при работе различных соединений (резьбовых, шлицевых, шпоночных).Условие прочности при сдвиге (срезе) имеет вид
- относительный сдвиг.С деформацией сдвига мы встречаемся при резании ножницами металла, при работе различных соединений (резьбовых, шлицевых, шпоночных).Условие прочности при сдвиге (срезе) имеет вид  .
.

 зависит от материала и вида соединения. Для неразъемных заклепочных соединений из деформируемых алюминиевых сплавов можно принять
зависит от материала и вида соединения. Для неразъемных заклепочных соединений из деформируемых алюминиевых сплавов можно принять  -в случае неподвижных соединений;
-в случае неподвижных соединений; Помимо среза заклепкам и соединяемым листам в конструкции угрожают и иные опасности.На рис.1 указана примерная схема передачи давлений на стержень заклепки. Закон распределения этих давлений по цилиндрической поверхности нам неизвестен; он во многом зависит от неправильностей формы заклепочного отверстиями стержня, вызванных условиями изготовления конструкции. Поэтому расчет производится условно. Принято считать, что неравномерное давление, передающееся на поверхность заклепки от листа, распределяется равномерно по диаметральной плоскости сечения заклепки. При этом напряжение по этой диаметральной плоскости оказывается примерно равным наибольшему сминающему напряжению
Помимо среза заклепкам и соединяемым листам в конструкции угрожают и иные опасности.На рис.1 указана примерная схема передачи давлений на стержень заклепки. Закон распределения этих давлений по цилиндрической поверхности нам неизвестен; он во многом зависит от неправильностей формы заклепочного отверстиями стержня, вызванных условиями изготовления конструкции. Поэтому расчет производится условно. Принято считать, что неравномерное давление, передающееся на поверхность заклепки от листа, распределяется равномерно по диаметральной плоскости сечения заклепки. При этом напряжение по этой диаметральной плоскости оказывается примерно равным наибольшему сминающему напряжению  в точке А поверхности заклепки.
в точке А поверхности заклепки. 
 Для определения крутящих моментов в сечениях пользуются методом сечений. Намечают участки бруса, рассекают его вооброжаемой плоскостью, мысленно отрбрасывают одну часть. К другой части прикладывают в сечении неизвестный крутящий момент, направляя его по ходу часовой стрелки и составляют уравнение равновесия, из которого находят значение Т.Положительными принимают скручивающие моменты, если они поворачивают отсеченную часть бруса против хода часовой стрелки. Знак крутящего момента бруса значения не имеет.Условимся считать Mz положительным, если со стороны отброшенной части стержня видим его направленным против часовой стрелки (рис. 2). Это правило проиллюстрировано на рис. 1 и в указанном соотношении, где крутящий момент Мz принят положительным. Численно крутящий момент равен сумме моментов внешних сил, приложенных к отсеченной части стержня, относительно оси Ог
Для определения крутящих моментов в сечениях пользуются методом сечений. Намечают участки бруса, рассекают его вооброжаемой плоскостью, мысленно отрбрасывают одну часть. К другой части прикладывают в сечении неизвестный крутящий момент, направляя его по ходу часовой стрелки и составляют уравнение равновесия, из которого находят значение Т.Положительными принимают скручивающие моменты, если они поворачивают отсеченную часть бруса против хода часовой стрелки. Знак крутящего момента бруса значения не имеет.Условимся считать Mz положительным, если со стороны отброшенной части стержня видим его направленным против часовой стрелки (рис. 2). Это правило проиллюстрировано на рис. 1 и в указанном соотношении, где крутящий момент Мz принят положительным. Численно крутящий момент равен сумме моментов внешних сил, приложенных к отсеченной части стержня, относительно оси Ог  Кручением называется простой вид сопротивления, при котором к брусу (валу) прикладываются внешние пары сил в плоскостях, совпадающих с поперечным сечением вала, а в последних возникает только внутренний крутящий момент.Рассмотрим расчетную схему вала, нагруженного двумя сосредоточенными моментами М и 2М и распределенными по длине: m, рис.2.Методика построения эпюры аналогична только что рассмотренной методике при растяжении-сжатии.
Кручением называется простой вид сопротивления, при котором к брусу (валу) прикладываются внешние пары сил в плоскостях, совпадающих с поперечным сечением вала, а в последних возникает только внутренний крутящий момент.Рассмотрим расчетную схему вала, нагруженного двумя сосредоточенными моментами М и 2М и распределенными по длине: m, рис.2.Методика построения эпюры аналогична только что рассмотренной методике при растяжении-сжатии.
 , которые для цилиндрического стержня можно определить по формуле
, которые для цилиндрического стержня можно определить по формуле  . Данное выражения явл. уравнением для построения графика, т.е. эпюры касательных напряжений в любом радиальном направлении круглого сечения.
. Данное выражения явл. уравнением для построения графика, т.е. эпюры касательных напряжений в любом радиальном направлении круглого сечения. 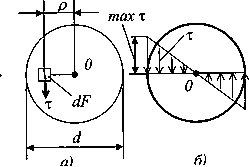
 — погонный угол закручивания стержня, который остается пока неизвестным. Для его нахождения обратимся к условию статики, записав его в более удобной для данного случая форме (рис. 6, a)
— погонный угол закручивания стержня, который остается пока неизвестным. Для его нахождения обратимся к условию статики, записав его в более удобной для данного случая форме (рис. 6, a) 
 , где WК = b 3 аналог полярного момента сопротивления поперечного сечения прямоугольного бруса; в точке В B max ,
, где WК = b 3 аналог полярного момента сопротивления поперечного сечения прямоугольного бруса; в точке В B max , , (4.16)
, (4.16)

 Ðèñ. 4.7
Ðèñ. 4.7
 , получим:
, получим:  ;
; 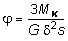 , где толщина профиля; s длина контура профиля; l длина стержня.В случае, если тонкостенный незамкнутый профиль является составным (рис. 4.8) и не может быть развернут в вытянутый прямоугольник, воспользовавшись почленной аналогией, легко определить выражения напряжений на i ом произвольном участке:
, где толщина профиля; s длина контура профиля; l длина стержня.В случае, если тонкостенный незамкнутый профиль является составным (рис. 4.8) и не может быть развернут в вытянутый прямоугольник, воспользовавшись почленной аналогией, легко определить выражения напряжений на i ом произвольном участке:  , (4.18)
, (4.18)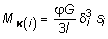 ,
, .рассмотрим брус, имеющий поперечное сечение в форме замкнутого тонкостенного профиля (рис. 4.9). Выделим на контуре элементарный участок длиной ds и выразим крутящий момент через напряжения , выполняя операцию контурного интегрирования получим:
.рассмотрим брус, имеющий поперечное сечение в форме замкнутого тонкостенного профиля (рис. 4.9). Выделим на контуре элементарный участок длиной ds и выразим крутящий момент через напряжения , выполняя операцию контурного интегрирования получим:  . (4.20)
. (4.20) ,
, представляет собой удвоенной площадь, ограниченную срединной линией контура сечения.Из (4.21) наибольшее напряжение определяет
представляет собой удвоенной площадь, ограниченную срединной линией контура сечения.Из (4.21) наибольшее напряжение определяет 


