
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экстремальные касательные напряженияСодержание книги
Поиск на нашем сайте Вырежем из тела, испытывающего ПНС, прямоугольный элемент с главными площадками, на которых действуют
Итак, экстремальные касательные напряжения действуют на площадках под углом 45° к главным и определяются по формулам (11.14) или (11.15). Нормальные напряжения
Здесь учтено, что § 11.9. Чистый сдвиг
Рассмотрим частный случай ПНС, когда главные напряжения В этом случае экстремальные
Такой случай носит название чистый сдвиг.
Из этих формул видно, что при Итак, при чистом сдвиге главные площадки расположены под углом 45° к площадкам чистого сдвига, а главные напряжения на них:
§ 11.10. Анализ деформированного состояния
напряженного состояния. Три взаимно ортогональных направления, сдвиги между которыми при деформации тела равны нулю, называются главными осями деформированного состояния. Линейные деформации по этим направлениям называются главными деформациями и обозначаются Главные деформации находятся из уравнения, аналогичного уравнению (11.5) для определения главных напряжений
Здесь
Решение кубического уравнения (11.17) дает три величины главных деформаций В случае плоской деформации, когда, например,
Экстремальные сдвиги находятся по формулам, аналогичным (11.7), для определения экстремальных касательных напряжений:
Для изотропных материалов направления главных деформаций совпадают с направлениями главных напряжений. Выясним физический смысл инварианта
Деформации
Итак, первый инвариант деформированного состояния определяет относительное изменение объема тела.
|
||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 472; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 и
и  (рис.11.5). Выделим наклонную площадку ab, нормаль
(рис.11.5). Выделим наклонную площадку ab, нормаль  к которой с направлением
к которой с направлением 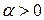 . Напряжения
. Напряжения  и
и  на этой площадке найдем по зависимостям (11.10) и (11.11), полагая
на этой площадке найдем по зависимостям (11.10) и (11.11), полагая  .
. Рис.11.5
Рис.11.5
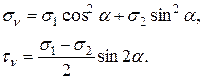 (18)
Из второй формулы (18) видно, что при
(18)
Из второй формулы (18) видно, что при 
 . (11.14)
Подставляя сюда
. (11.14)
Подставляя сюда 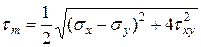 . (11.15)
. (11.15)
 на этих площадках найдем по первой формуле (18), подставляя
на этих площадках найдем по первой формуле (18), подставляя  ):
): . (19)
. (19) .
. .
. найдем по (11.14), а нормальные напряжения
найдем по (11.14), а нормальные напряжения  на этих площадках по (19). Итак
на этих площадках по (19). Итак .
. Рис. 11.6
Рис. 11.6
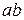 под углом
под углом  (рис. 11.6). Используя формулы (11.10) и (11.11), подставляя в них:
(рис. 11.6). Используя формулы (11.10) и (11.11), подставляя в них:  ,
,  , получим:
, получим:
 . (11.16)
. (11.16)
 , а это, как известно, характеристики главной площадки.
, а это, как известно, характеристики главной площадки.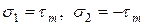 (при
(при  ).
). Рис.11.7
Рис.11.7
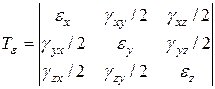 .
Тензор деформации
.
Тензор деформации  (1.4) представим в симметричном виде (рис.11.7), когда
(1.4) представим в симметричном виде (рис.11.7), когда 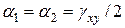 и т.д. Анализ деформи-рованного состояния проведем по аналогии с вышеприведенным анализом
и т.д. Анализ деформи-рованного состояния проведем по аналогии с вышеприведенным анализом
 .
. . (11.17)
. (11.17) и
и  инварианты деформированного состояния:
инварианты деформированного состояния: (11.18)
(11.18) .
. по аналогии с ПНС формулы (11.12), получим
по аналогии с ПНС формулы (11.12), получим  и
и  :
: . (11.19)
. (11.19) (11.20)
(11.20)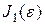 : Рассмотрим кубик, у которого ребра совпадают с направлениями главных деформаций и до нагружения тела их длины равны 1. Его объем
: Рассмотрим кубик, у которого ребра совпадают с направлениями главных деформаций и до нагружения тела их длины равны 1. Его объем  . После деформации его объем станет
. После деформации его объем станет  . Относительное изменение объема обозначим
. Относительное изменение объема обозначим 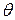 :
: ,
,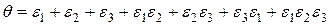 .
. . (11.21)
. (11.21)


